Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-16T10:40:28.687Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on the Uniqueness Theorem of Solutions of the Darboux Problem

Published online by Cambridge University Press:  20 November 2018

James S. W. Wong
James S. W. Wong*
Affiliation:
University of Alberta, Edmonton
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Recently B. Palczewski and W. Pawelski [l] have given some sufficient conditions of uniqueness for the solutions of the Darboux problem for equations of the form:

1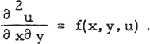

The criteria given there for equations of the form (1) are natural generalizations of the criteria given by Krasnosielski and Krein [2] in the corresponding ordinary differential case. The purpose of the present note is to give a further generalization of the above result and two other uniqueness conditions for the solutions of the Darboux problem of the same form.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 8 , Issue 6 , December 1965 , pp. 791 - 796
Copyright
Copyright © Canadian Mathematical Society 1965

References

1. Palczewski, B. and Pawelski, W., Some remarks on the uniqueness of solutions to the Darboux problem with conditions of the Krasnosielski-Krein type, Ann. Polon. Math. XIV (1964), pp. 97-100.Google Scholar
2. Krasnosielski, M. A. and Krein, S. G., On a class of uniqueness theorems for the equation y' = f(x, y), Uspehi Mat. Nauk. (N.S.)11 (1956), No.1 (67), 209-213.Google Scholar
3. Kooi, O., The method of successive approximations and a uniqueness theorem of Krasnosielski and Krein in the theory of differential equations, Indag. Math. 20 (1958), pp.322-327.Google Scholar
4. Kooi, O., Existentie, eenduidigheids- en convergentie stellingen in de théorie der gewone differentiaal vergelijkingen, Thesis V. U., Amsterdem (1956).Google Scholar
5. Nagumo, M., Eine hinreichende Bedingung für die Unität der Lösung von Differentialgleichungen erster Ordnung, Japan J. Math. 3 (1926) pp. 107-112.Google Scholar