Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T21:29:08.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Restriction Operators Acting on Radial Functions on Vector Spaces over Finite Fields

Published online by Cambridge University Press:  20 November 2018

Doowon Koh
Doowon Koh*
Affiliation:
Department of Mathematics, Chungbuk National University, Cheongju city, Chungbuk-Do 361-763 Korea e-mail: koh131@chungbuk.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study 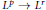${{L}^{p}}\to {{L}^{r}}$ restriction estimates for algebraic varieties 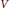$V$ in the case when restriction operators act on radial functions in the finite field setting. We show that if the varieties 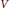$V$ lie in odd dimensional vector spaces over finite fields, then the conjectured restriction estimates are possible for all radial test functions. In addition, assuming that the varieties 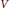$V$ are defined in even dimensional spaces and have few intersection points with the sphere of zero radius, we also obtain the conjectured exponents for all radial test functions.

Keywords

42B0543A3243A15finite fieldsradial functionsrestriction operators.
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 4 , 01 December 2014 , pp. 834 - 844
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Barcelo, B., On the restriction of the Fourier transform to a conical surface. Trans. Amer. Math. Soc. 292 (1985), 321–333. http://dx.doi.org/10.1090/S0002-9947-1985-0805965-8 Google Scholar
[2] Bourgain, J., On the restriction and multiplier problem in R3. In: Geometric aspects of functional analysis (1989–90), Lecture Notes in Math. 1469, Springer-Verlag, Berlin, 1991, 179–191.Google Scholar
[3] Carbery, A., Harmonic analysis on vector spaces over finite fields. Lecture notes, 2006. http://www.maths.ed.ac.uk/_carbery/analysis/notes/fflpublic.pdf.Google Scholar
[4] Fefferman, C., Inequalities for strongly singular convolution operators. Acta Math. 124 (1970), 9–36. http://dx.doi.org/10.1007/BF02394567 Google Scholar
[5] De Carli, L. and Grafakos, L., On the restriction conjecture. Michigan Math. J. 52 (2004), 163–180. http://dx.doi.org/10.1307/mmj/1080837741 Google Scholar
[6] Hart, D., Iosevich, A., Koh, D., and Rudnev, M., Averages over hyperplanes, sum-product theory in vector spaces over finite fields and the Erdös–Falconer distance conjecture. Trans. Amer. Math. Soc. 363 (2011), 3255–3275. http://dx.doi.org/10.1090/S0002-9947-2010-05232-8 Google Scholar
[7] Iosevich, A. and Koh, D., Extension theorems for paraboloids in the finite field setting. Math. Z. 266 (2010), 471–487. http://dx.doi.org/10.1007/s00209-009-0580-1 Google Scholar
[8] Iosevich, A. and Koh, D., Extension theorems for spheres in the finite field setting. Forum. Math. 22 (2010), 457–483.Google Scholar
[9] Iosevich, A. and Rudnev, M., Erdʺos distance problem in vector spaces over finite fields. Trans. Amer. Math. Soc. 359 (2007), 6127–6142. http://dx.doi.org/10.1090/S0002-9947-07-04265-1 Google Scholar
[10] Iwaniec, H. and Kowalski, E., Analytic number theory. Amer. Math. Soc. Colloq. Publ. 53, Amer. Math. Soc., Providence, RI, 2004.Google Scholar
[11] Koh, D. and Shen, C., Sharp extension theorems and Falconer distance problems for algebraic curves in two dimensional vector spaces over finite fields. Rev. Mat. Iberoam. 28 (2012), 157–178.Google Scholar
[12] Lewko, M., New restriction estimates for the 3-d paraboloid over finite fields. arxiv:1302.6664.Google Scholar
[13] Lewko, A. and Lewko, M., Endpoint restriction estimates for the paraboloid over finite fields. Proc. Amer. Math. Soc. 140 (2012), 2013–2028. http://dx.doi.org/10.1090/S0002-9939-2011-11444-8 Google Scholar
[14] Lidl, R. and Niederreiter, H., Finite fields. Cambridge University Press, Cambridge, 1997.Google Scholar
[15] Mockenhaupt, G. and Tao, T., Restriction and Kakeya phenomena for finite fields. Duke Math. J. 121 (2004), 35–74. http://dx.doi.org/10.1215/S0012-7094-04-12112-8 Google Scholar
[16] Stein, E. M., Harmonic Analysis. Princeton University Press, Princeton, NJ, 1993.Google Scholar
[17] Tao, T., A sharp bilinear restriction estimate for paraboloids. Geom. Funct. Anal. 13 (2003), 1359–1384. http://dx.doi.org/10.1007/s00039-003-0449-0 Google Scholar
[18] Tao, T., Some recent progress on the restriction conjecture. In: Fourier analysis and convexity, Appl. Numer. Harmon. Anal., Birkhäuser Boston, Boston, MA, 2004, 217–243.Google Scholar
[19] Wolff, T., A sharp bilinear cone restriction estimate. Ann. of Math. 153 (2001), 661–698. http://dx.doi.org/10.2307/2661365 Google Scholar
[20] Wolff, T., Lectures on Harmonic Analysis. Univ. Lecture Ser. 29, American Mathematical Society, Providence, RI, 2003.Google Scholar
[21] Zygmund, A., On Fourier coefficients and transforms of functions of two variables. Studia Math. 50 (1974), 189–201.Google Scholar