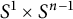1 Introduction
Throughout this paper, we assume
![]() $n\geq 3$
. Let
$n\geq 3$
. Let
![]() $g_{S^n}$
be the standard metric on the n-dimensional unit sphere
$g_{S^n}$
be the standard metric on the n-dimensional unit sphere
![]() $S^n$
. Answering a question of Gromov [Reference Gromov5], Llarull [Reference Llarull11] proved the following:
$S^n$
. Answering a question of Gromov [Reference Gromov5], Llarull [Reference Llarull11] proved the following:
Theorem 1.1 (Theorem A in [Reference Llarull11])
Suppose g is a Riemannian metric on
![]() $S^n$
such that its scalar curvature
$S^n$
such that its scalar curvature
![]() $R_g\geq n(n-1)=R_{g_{S^n}}$
and
$R_g\geq n(n-1)=R_{g_{S^n}}$
and
![]() $g\geq g_{S^n}$
. Then we must have
$g\geq g_{S^n}$
. Then we must have
![]() $g=g_{S^n}$
.
$g=g_{S^n}$
.
In the even-dimensional case, Listing [Reference Listing9] was able to generalize Theorem 1.1 as follows:
Theorem 1.2 Let
![]() $n\geq 4$
be an even integer. Moreover, suppose that g is a Riemannian metric on
$n\geq 4$
be an even integer. Moreover, suppose that g is a Riemannian metric on
![]() $S^n$
satisfying
$S^n$
satisfying
![]() $R_g\geq (n -1) tr_g(g_{S^n})$
at each point on
$R_g\geq (n -1) tr_g(g_{S^n})$
at each point on
![]() $S^n$
. Then g is a constant multiple of
$S^n$
. Then g is a constant multiple of
![]() $g_{S^n}$
.
$g_{S^n}$
.
Later, rigidity results related to the scalar curvature, including compact symmetric spaces, have been obtain by other authors in [Reference Goette and Semmelmann3, Reference Goette and Semmelmann4, Reference Llarull10, Reference Min-Oo12]. For more rigidity results involving scalar curvature, we refer the readers to the survey [Reference Brendle1].
For any
![]() $c>0$
, let
$c>0$
, let
![]() $g_c$
be the product metric given by
$g_c$
be the product metric given by
![]() $g_c=c\,ds^2+g_{S^{n-1}}$
on the product of spheres
$g_c=c\,ds^2+g_{S^{n-1}}$
on the product of spheres
![]() $S^1\times S^{n-1}$
. In this paper, we prove the following:
$S^1\times S^{n-1}$
. In this paper, we prove the following:
Theorem 1.3 Suppose g is a Riemannian metric on
![]() $S^1\times S^{n-1}$
such that:
$S^1\times S^{n-1}$
such that:
(i) its scalar curvature
![]() $R_g\geq (n-1)(n-2)=R_{g_c}$
,
$R_g\geq (n-1)(n-2)=R_{g_c}$
,
(ii)
![]() $g\geq g_c$
, and
$g\geq g_c$
, and
(iii) its Ricci curvature
![]() $Ric_g\geq 0$
.
$Ric_g\geq 0$
.
Then g is isometric to
![]() $g_{\tilde {c}}$
for some
$g_{\tilde {c}}$
for some
![]() $\tilde {c}\geq c$
.
$\tilde {c}\geq c$
.
Compared to that of Theorems 1.1 and 1.2, the assumption of Ricci curvature in Theorem 1.3 may seem to be strong. But we remark that lower bound on the Ricci curvature is assumed when rigidity result of symmetric space is studied. See Theorem 0.2 in [Reference Goette and Semmelmann3].
In Section 2, we prove a conformal version of Theorem 1.3. See Corollary 2.2 for the precise statement. Note that the similar idea can be used to prove rigidity results for manifolds with boundary and for CR manifolds within a fixed conformal class. See Propositions 2.3 and 2.5.
In Section 3, we prove Theorem 1.3. We then provide examples showing that neither assumption (i) nor assumption (ii) could be dropped in Theorem 1.3. This leaves us the question whether assumption (iii) on Ricci curvature could be dropped in Theorem 1.3. While we are not able to answer it, we are able to prove a rigidity result of warped product metric without any assumption on Ricci curvature. See Theorem 3.1 for the precise statement.
2 A conformal version
As a warm-up, we will prove in this section a conformal version of Theorem 1.3. We first prove the following more general proposition.
Proposition 2.1. Suppose
![]() $(M,\tilde {g})$
is a closed (i.e., compact without boundary) Riemannian manifold such that its scalar curvature satisfies
$(M,\tilde {g})$
is a closed (i.e., compact without boundary) Riemannian manifold such that its scalar curvature satisfies
![]() $R_{\tilde {g}}\geq 0$
and
$R_{\tilde {g}}\geq 0$
and
![]() $R_{\tilde {g}}\not \equiv 0$
. If g is conformal to
$R_{\tilde {g}}\not \equiv 0$
. If g is conformal to
![]() $\tilde {g}$
such that
$\tilde {g}$
such that
![]() $g\geq \tilde {g}$
and
$g\geq \tilde {g}$
and
![]() $R_g\geq R_{\tilde {g}}$
, then
$R_g\geq R_{\tilde {g}}$
, then
![]() $g=\tilde {g}$
.
$g=\tilde {g}$
.
Proof Since g is conformal to
![]() $\tilde {g}$
, we can write
$\tilde {g}$
, we can write
![]() $g=u^{\frac {4}{n-2}}\tilde {g}$
for some
$g=u^{\frac {4}{n-2}}\tilde {g}$
for some
![]() $0<u\in C^\infty (M)$
. By the assumption that
$0<u\in C^\infty (M)$
. By the assumption that
![]() $g\geq \tilde {g}$
, we have
$g\geq \tilde {g}$
, we have
Moreover, since
![]() $g=u^{\frac {4}{n-2}}\tilde {g}$
, it is well known that
$g=u^{\frac {4}{n-2}}\tilde {g}$
, it is well known that
By (2.2) and the assumption that
![]() $R_g\geq R_{\tilde {g}}$
, we find
$R_g\geq R_{\tilde {g}}$
, we find
 $$ \begin{align} \nonumber -\frac{4(n-1)}{n-2}\Delta_{\tilde{g}} u &=R_gu^{\frac{n+2}{n-2}}-R_{\tilde{g}} u \\ &\geq R_{\tilde{g}}u^{\frac{n+2}{n-2}}-R_{\tilde{g}} u =R_{\tilde{g}}u^{\frac{4}{n-2}}(u-1). \end{align} $$
$$ \begin{align} \nonumber -\frac{4(n-1)}{n-2}\Delta_{\tilde{g}} u &=R_gu^{\frac{n+2}{n-2}}-R_{\tilde{g}} u \\ &\geq R_{\tilde{g}}u^{\frac{n+2}{n-2}}-R_{\tilde{g}} u =R_{\tilde{g}}u^{\frac{4}{n-2}}(u-1). \end{align} $$
It follows from (2.1) and the assumption that
![]() $R_{\tilde {g}}\geq 0$
that the last term in (2.3) is nonnegative, which gives
$R_{\tilde {g}}\geq 0$
that the last term in (2.3) is nonnegative, which gives
![]() $\Delta _{\tilde {g}} u\leq 0$
in M. Since M is compact, we must have
$\Delta _{\tilde {g}} u\leq 0$
in M. Since M is compact, we must have
for some constant c. On one hand, it follows from (2.1) that
![]() $c\geq 1$
. On the other hand, by (2.2) and the assumption that
$c\geq 1$
. On the other hand, by (2.2) and the assumption that
![]() $R_g\geq R_{\tilde {g}}$
, we deduce
$R_g\geq R_{\tilde {g}}$
, we deduce
Since
![]() $R_{\tilde {g}}\geq 0$
and
$R_{\tilde {g}}\geq 0$
and
![]() $R_{\tilde {g}}\not \equiv 0$
, we have
$R_{\tilde {g}}\not \equiv 0$
, we have
![]() $c\leq 1$
. That is to say, we have
$c\leq 1$
. That is to say, we have
![]() $c=1$
and
$c=1$
and
![]() $u\equiv 1$
, or equivalently,
$u\equiv 1$
, or equivalently,
![]() $g=\tilde {g}$
, as claimed.
$g=\tilde {g}$
, as claimed.
For the product metric
![]() $g_c=c\,ds^2+g_{S^{n-1}}$
on the product of spheres
$g_c=c\,ds^2+g_{S^{n-1}}$
on the product of spheres
![]() $S^1\times S^{n-1}$
, the scalar curvature of
$S^1\times S^{n-1}$
, the scalar curvature of
![]() $g_c$
is equal to
$g_c$
is equal to
![]() $(n-1)(n-2)$
. Therefore, we can apply Proposition 2.1 with
$(n-1)(n-2)$
. Therefore, we can apply Proposition 2.1 with
![]() $(M,\tilde {g})=(S^1\times S^{n-1}, g_c)$
to get the following corollary, which is a conformal version of Theorem 1.3.
$(M,\tilde {g})=(S^1\times S^{n-1}, g_c)$
to get the following corollary, which is a conformal version of Theorem 1.3.
Corollary 2.2. If g is a metric on
![]() $S^1{\kern-1pt}\times{\kern-1pt} S^{n-1}$
conformal to
$S^1{\kern-1pt}\times{\kern-1pt} S^{n-1}$
conformal to
![]() $g_c$
such that
$g_c$
such that
![]() $R_g{\kern-1pt}\geq{\kern-1pt} R_{g_c}{\kern-1pt}={\kern-1pt}(n-1) (n-2)$
and
$R_g{\kern-1pt}\geq{\kern-1pt} R_{g_c}{\kern-1pt}={\kern-1pt}(n-1) (n-2)$
and
![]() $g\geq g_c$
, then
$g\geq g_c$
, then
![]() $g=g_c$
.
$g=g_c$
.
Note that there is no assumption on the Ricci curvature in Corollary 2.2. The idea of the proof of Proposition 2.1 can be used to prove the following:
Proposition 2.3. Suppose
![]() $(M,\tilde {g})$
is a compact Riemannian manifold with boundary
$(M,\tilde {g})$
is a compact Riemannian manifold with boundary
![]() $\partial M$
such that its scalar curvature satisfies
$\partial M$
such that its scalar curvature satisfies
![]() $R_{\tilde {g}}\geq 0$
and
$R_{\tilde {g}}\geq 0$
and
![]() $R_{\tilde {g}}\not \equiv 0$
in M and its mean curvature satisfies
$R_{\tilde {g}}\not \equiv 0$
in M and its mean curvature satisfies
![]() $H_{\tilde {g}}=0$
on
$H_{\tilde {g}}=0$
on
![]() $\partial M$
. If g is conformal to
$\partial M$
. If g is conformal to
![]() $\tilde {g}$
such that
$\tilde {g}$
such that
![]() $g\geq \tilde {g}$
,
$g\geq \tilde {g}$
,
![]() $R_g\geq R_{\tilde {g}}$
in M, and
$R_g\geq R_{\tilde {g}}$
in M, and
![]() $H_g=0$
on
$H_g=0$
on
![]() $\partial M$
, then
$\partial M$
, then
![]() $g=\tilde {g}$
.
$g=\tilde {g}$
.
Proof Since the proof is very similar to Proposition 2.1, we only sketch it. If we write
![]() $g=u^{\frac {4}{n-2}}\tilde {g}$
for some
$g=u^{\frac {4}{n-2}}\tilde {g}$
for some
![]() $0<u\in C^\infty (M)$
, we still have (2.1). Since
$0<u\in C^\infty (M)$
, we still have (2.1). Since
![]() $g=u^{\frac {4}{n-2}}\tilde {g}$
, we have (see, for example, [Reference Escobar2])
$g=u^{\frac {4}{n-2}}\tilde {g}$
, we have (see, for example, [Reference Escobar2])
 $$ \begin{align} \nonumber -\frac{4(n-1)}{n-2}\Delta_{\tilde{g}} u+R_{\tilde{g}} u&=R_gu^{\frac{n+2}{n-2}}~~\text{ in }M, \\ \frac{2(n-1)}{n-2}\frac{\partial u}{\partial\nu_{\tilde{g}}}+H_{\tilde{g}} u&=H_g u^{\frac{n}{n-2}}~~\text{ on }\partial M. \end{align} $$
$$ \begin{align} \nonumber -\frac{4(n-1)}{n-2}\Delta_{\tilde{g}} u+R_{\tilde{g}} u&=R_gu^{\frac{n+2}{n-2}}~~\text{ in }M, \\ \frac{2(n-1)}{n-2}\frac{\partial u}{\partial\nu_{\tilde{g}}}+H_{\tilde{g}} u&=H_g u^{\frac{n}{n-2}}~~\text{ on }\partial M. \end{align} $$
It follows from the second equation in (2.4) and the assumption that
![]() $H_g=H_{\tilde {g}}=0$
that
$H_g=H_{\tilde {g}}=0$
that
 $$ \begin{align} \frac{\partial u}{\partial\nu_{\tilde{g}}}=0~~\text{ on }\partial M. \end{align} $$
$$ \begin{align} \frac{\partial u}{\partial\nu_{\tilde{g}}}=0~~\text{ on }\partial M. \end{align} $$
Following the proof of Proposition 2.1, we can conclude that
Combining this with (2.5), we can conclude that
![]() $u\equiv c$
for some constant c. As in the proof of Proposition 2.1, we can then conclude that
$u\equiv c$
for some constant c. As in the proof of Proposition 2.1, we can then conclude that
![]() $u\equiv 1$
, or equivalently,
$u\equiv 1$
, or equivalently,
![]() $g=\tilde {g}$
.
$g=\tilde {g}$
.
Let
![]() $(M,g_0)$
be a closed (i.e., compact without boundary) n-dimensional Riemannian manifold such that its scalar curvature
$(M,g_0)$
be a closed (i.e., compact without boundary) n-dimensional Riemannian manifold such that its scalar curvature
![]() $R_{g_0}\geq 0$
and
$R_{g_0}\geq 0$
and
![]() $R_{g_0}\not \equiv 0$
. Then
$R_{g_0}\not \equiv 0$
. Then
![]() $[0,1]\times M$
is a compact
$[0,1]\times M$
is a compact
![]() $(n+1)$
-dimensional manifold with boundary
$(n+1)$
-dimensional manifold with boundary
![]() $(\{0\}\times M)\cup (\{1\}\times M)$
. Equipped with the product metric
$(\{0\}\times M)\cup (\{1\}\times M)$
. Equipped with the product metric
![]() $ds^2+g_0$
,
$ds^2+g_0$
,
![]() $[0,1]\times M$
has scalar curvature being equal to
$[0,1]\times M$
has scalar curvature being equal to
![]() $R_{g_0}$
and has vanishing mean curvature. Therefore, we can apply Proposition 2.3 to get the following:
$R_{g_0}$
and has vanishing mean curvature. Therefore, we can apply Proposition 2.3 to get the following:
Corollary 2.4. Let
![]() $(M,g_0)$
be a closed (i.e., compact without boundary) n-dimensional Riemannian manifold such that its scalar curvature
$(M,g_0)$
be a closed (i.e., compact without boundary) n-dimensional Riemannian manifold such that its scalar curvature
![]() $R_{g_0}\geq 0$
and
$R_{g_0}\geq 0$
and
![]() $R_{g_0}\not \equiv 0$
. If g is a metric on
$R_{g_0}\not \equiv 0$
. If g is a metric on
![]() $[0,1]\times M$
conformal to
$[0,1]\times M$
conformal to
![]() $\tilde {g}=ds^2+g_0$
such that
$\tilde {g}=ds^2+g_0$
such that
![]() $g\geq \tilde {g}$
,
$g\geq \tilde {g}$
,
![]() $R_g\geq R_{\tilde {g}}$
in M, and
$R_g\geq R_{\tilde {g}}$
in M, and
![]() $H_g=0$
on
$H_g=0$
on
![]() $\partial M$
, then
$\partial M$
, then
![]() $g=\tilde {g}$
.
$g=\tilde {g}$
.
Similarly, one can prove the following CR version of Proposition 2.1. Basic facts about CR manifolds could be found in [Reference Jerison and Lee7] for example.
Proposition 2.5. Suppose that
![]() $(M,\tilde {\theta })$
is a compact strictly pseudoconvex CR manifold of real dimension
$(M,\tilde {\theta })$
is a compact strictly pseudoconvex CR manifold of real dimension
![]() $2N+1$
with a given contact form
$2N+1$
with a given contact form
![]() $\tilde {\theta }$
such that its Webster scalar curvature satisfies
$\tilde {\theta }$
such that its Webster scalar curvature satisfies
![]() $R_{\tilde {\theta }}\geq 0$
and
$R_{\tilde {\theta }}\geq 0$
and
![]() $R_{\tilde {\theta }}\not \equiv 0$
. If
$R_{\tilde {\theta }}\not \equiv 0$
. If
![]() $\theta $
is conformal to
$\theta $
is conformal to
![]() $\tilde {\theta }$
such that
$\tilde {\theta }$
such that
![]() $\theta \geq \tilde {\theta }$
and
$\theta \geq \tilde {\theta }$
and
![]() $R_\theta \geq R_{\tilde {\theta }}$
, then
$R_\theta \geq R_{\tilde {\theta }}$
, then
![]() $\theta =\tilde {\theta }$
.
$\theta =\tilde {\theta }$
.
Proof Since
![]() $\theta $
is conformal to
$\theta $
is conformal to
![]() $\tilde {\theta }$
, we can write
$\tilde {\theta }$
, we can write
![]() $\theta =u^{\frac {2}{N}}\tilde {\theta }$
for some
$\theta =u^{\frac {2}{N}}\tilde {\theta }$
for some
![]() $0<u\in C^\infty (M)$
. We then have
$0<u\in C^\infty (M)$
. We then have
since
![]() $\theta \geq \tilde {\theta }$
by assumption. Since
$\theta \geq \tilde {\theta }$
by assumption. Since
![]() $\theta =u^{\frac {2}{N}}\tilde {\theta }$
, we have (cf. [Reference Jerison and Lee7])
$\theta =u^{\frac {2}{N}}\tilde {\theta }$
, we have (cf. [Reference Jerison and Lee7])
where
![]() $\Delta _{\tilde {\theta }}$
is the sub-Laplacian of
$\Delta _{\tilde {\theta }}$
is the sub-Laplacian of
![]() $\tilde {\theta }$
. Using (2.7) and the assumption that
$\tilde {\theta }$
. Using (2.7) and the assumption that
![]() $R_\theta \geq R_{\tilde {\theta }}$
, we deduce
$R_\theta \geq R_{\tilde {\theta }}$
, we deduce
 $$ \begin{align} \nonumber -\left(2+\frac{2}{N}\right)\Delta_{\tilde{\theta}}u &=R_\theta u^{1+\frac{2}{N}}-R_{\tilde{\theta}}u \\ &\geq R_{\tilde{\theta}}u^{1+\frac{2}{N}}-R_{\tilde{\theta}}u = R_{\tilde{\theta}}u^{\frac{2}{N}}(u-1). \end{align} $$
$$ \begin{align} \nonumber -\left(2+\frac{2}{N}\right)\Delta_{\tilde{\theta}}u &=R_\theta u^{1+\frac{2}{N}}-R_{\tilde{\theta}}u \\ &\geq R_{\tilde{\theta}}u^{1+\frac{2}{N}}-R_{\tilde{\theta}}u = R_{\tilde{\theta}}u^{\frac{2}{N}}(u-1). \end{align} $$
From (2.7) and the assumption that
![]() $R_{\tilde {\theta }}\geq 0$
, we can see that the last term in (2.8) is nonnegative, which implies that
$R_{\tilde {\theta }}\geq 0$
, we can see that the last term in (2.8) is nonnegative, which implies that
![]() $\Delta _{\tilde {\theta }}u\leq 0$
. Since M is compact, we have
$\Delta _{\tilde {\theta }}u\leq 0$
. Since M is compact, we have
for some constant c. Note that
![]() $c\geq 1$
by (2.6). Note also that
$c\geq 1$
by (2.6). Note also that
by (2.7) and the assumption
![]() $R_\theta \geq R_{\tilde {\theta }}$
. Since
$R_\theta \geq R_{\tilde {\theta }}$
. Since
![]() $R_{\tilde {\theta }}\geq 0$
and
$R_{\tilde {\theta }}\geq 0$
and
![]() $R_{\tilde {\theta }}\not \equiv 0$
, we must have
$R_{\tilde {\theta }}\not \equiv 0$
, we must have
![]() $c\leq 1$
. Hence, we have
$c\leq 1$
. Hence, we have
![]() $c=1$
and
$c=1$
and
![]() $u\equiv 1$
, which gives
$u\equiv 1$
, which gives
![]() $\theta =\tilde {\theta }$
.
$\theta =\tilde {\theta }$
.
The unit sphere
![]() $S^{2N+1}$
in
$S^{2N+1}$
in
![]() $\mathbb {C}^{N+1}=\{(z_1,...,z_{N+1})): z_i\in \mathbb {C}\}$
has a standard contact form given by
$\mathbb {C}^{N+1}=\{(z_1,...,z_{N+1})): z_i\in \mathbb {C}\}$
has a standard contact form given by
 $$ \begin{align*}\theta_0=\sqrt{-1}\sum_{j=1}^{N+1}(z_jd\overline{z}_j-\overline{z}_j dz_j).\end{align*} $$
$$ \begin{align*}\theta_0=\sqrt{-1}\sum_{j=1}^{N+1}(z_jd\overline{z}_j-\overline{z}_j dz_j).\end{align*} $$
Then the Webster scalar curvature of
![]() $(S^{2N+1}, \theta _0)$
is equal to
$(S^{2N+1}, \theta _0)$
is equal to
![]() $R_{\theta _0}=N(N+1)/2$
(see, for example, [Reference Ho6]). The following corollary follows from Proposition 2.5 by putting
$R_{\theta _0}=N(N+1)/2$
(see, for example, [Reference Ho6]). The following corollary follows from Proposition 2.5 by putting
![]() $(M,\tilde {\theta })=(S^{2N+1}, \theta _0)$
:
$(M,\tilde {\theta })=(S^{2N+1}, \theta _0)$
:
Corollary 2.6. Let
![]() $(S^{2N+1}, \theta _0)$
be the standard CR sphere equipped with the standard contact form
$(S^{2N+1}, \theta _0)$
be the standard CR sphere equipped with the standard contact form
![]() $\theta _0$
. If
$\theta _0$
. If
![]() $\theta $
is conformal to
$\theta $
is conformal to
![]() $\theta _0$
such that
$\theta _0$
such that
![]() $R_\theta \geq R_{\theta _0}=N(N+1)/2$
and
$R_\theta \geq R_{\theta _0}=N(N+1)/2$
and
![]() $\theta \geq \theta _0$
, then
$\theta \geq \theta _0$
, then
![]() $\theta =\theta _0$
.
$\theta =\theta _0$
.
3 Proof of Theorem 1.3
In this section, we prove Theorem 1.3.
Proof of Theorem 1.3
Consider the universal covering
![]() $\mathbb {R}\times S^{n-1}$
of
$\mathbb {R}\times S^{n-1}$
of
![]() $S^1\times S^{n-1}$
. The pullback of the metric g on
$S^1\times S^{n-1}$
. The pullback of the metric g on
![]() $S^1\times S^{n-1}$
under the covering map gives a metric
$S^1\times S^{n-1}$
under the covering map gives a metric
![]() $\overline {g}$
on
$\overline {g}$
on
![]() $\mathbb {R}\times S^{n-1}$
. By assumption (iii), the compact manifold
$\mathbb {R}\times S^{n-1}$
. By assumption (iii), the compact manifold
![]() $(S^1\times S^{n-1}, g)$
has nonnegative Ricci curvature. By Theorem 2.5 in Chapter I of [Reference Schoen and Yau13], the universal covering
$(S^1\times S^{n-1}, g)$
has nonnegative Ricci curvature. By Theorem 2.5 in Chapter I of [Reference Schoen and Yau13], the universal covering
![]() $(\mathbb {R}\times S^{n-1},\overline {g})$
of
$(\mathbb {R}\times S^{n-1},\overline {g})$
of
![]() $S^1\times S^{n-1}$
is isometric to
$S^1\times S^{n-1}$
is isometric to
![]() $\mathbb {R}^k\times M$
equipped with the product metric, where M is a compact
$\mathbb {R}^k\times M$
equipped with the product metric, where M is a compact
![]() $(n-k)$
-dimensional manifold. Hence, we must have
$(n-k)$
-dimensional manifold. Hence, we must have
![]() $k=1$
, and the metric
$k=1$
, and the metric
![]() $\overline {g}$
is isometric to the product metric
$\overline {g}$
is isometric to the product metric
![]() $ds^2+\tilde {g}$
on
$ds^2+\tilde {g}$
on
![]() $\mathbb {R}\times S^{n-1}$
, where
$\mathbb {R}\times S^{n-1}$
, where
![]() $\tilde {g}$
is a metric on
$\tilde {g}$
is a metric on
![]() $S^{n-1}$
. Therefore, the metric g, which is the metric
$S^{n-1}$
. Therefore, the metric g, which is the metric
![]() $\overline {g}$
descending on
$\overline {g}$
descending on
![]() $S^1\times S^{n-1}$
through the covering map, is isometric to the product metric
$S^1\times S^{n-1}$
through the covering map, is isometric to the product metric
![]() $\tilde {c}\,ds^2+\tilde {g}$
on
$\tilde {c}\,ds^2+\tilde {g}$
on
![]() $S^1\times S^{n-1}$
, where
$S^1\times S^{n-1}$
, where
![]() $\tilde {c}$
is a positive real number and
$\tilde {c}$
is a positive real number and
![]() $\tilde {g}$
is a metric on
$\tilde {g}$
is a metric on
![]() $S^{n-1}$
. As a result, up to isometry, we can assume that
$S^{n-1}$
. As a result, up to isometry, we can assume that
By assumption (ii), we have
![]() $g\geq g_c$
, which together with (3.1) implies that
$g\geq g_c$
, which together with (3.1) implies that
From this, we have
In view of (3.1), the scalar curvature of g is equal to the scalar of
![]() $\tilde {g}$
, i.e.,
$\tilde {g}$
, i.e.,
![]() $R_{\tilde {g}}=R_g.$
Combining this with assumption (i), we have
$R_{\tilde {g}}=R_g.$
Combining this with assumption (i), we have
In view of (3.3) and the second condition in (3.2), we can apply Llarull’s result in Theorem 1.1 to conclude that
![]() $\tilde {g}=g_{S^{n-1}}$
. Now the assertion follows from this, (3.1), and the first condition in (3.2).
$\tilde {g}=g_{S^{n-1}}$
. Now the assertion follows from this, (3.1), and the first condition in (3.2).
The following example shows that some assumptions in Theorem 1.3 could not be dropped. Consider the product metric
on
![]() $S^1\times S^{n-1}$
, where
$S^1\times S^{n-1}$
, where
![]() $c_1$
is a positive constant to be chosen. Then the Ricci curvature of g is nonnegative. In particular, assumption (iii) in Theorem 1.3 is satisfied. Moreover, the scalar curvature of g is equal to
$c_1$
is a positive constant to be chosen. Then the Ricci curvature of g is nonnegative. In particular, assumption (iii) in Theorem 1.3 is satisfied. Moreover, the scalar curvature of g is equal to
When
![]() $c_1\neq 1$
, it follows from (3.4) that g is not isometric to
$c_1\neq 1$
, it follows from (3.4) that g is not isometric to
![]() $g_c=cds^2+g_{S^{n-1}}$
for any
$g_c=cds^2+g_{S^{n-1}}$
for any
![]() $c>0$
, since the scalar curvature of
$c>0$
, since the scalar curvature of
![]() $g_c$
is equal to
$g_c$
is equal to
![]() $(n-1)(n-2)$
. Therefore, if
$(n-1)(n-2)$
. Therefore, if
![]() $c_1>1$
, then
$c_1>1$
, then
i.e., assumption (ii) in Theorem 1.3 is satisfied, and by (3.4)
i.e., assumption (iii) in Theorem 1.3 is not satisfied. To conclude, we see that assumption (iii) in Theorem 1.3 cannot be dropped. On the other hand, if
![]() $c_1<1$
, then
$c_1<1$
, then
i.e., assumption (ii) in Theorem 1.3 is not satisfied, and by (3.4)
i.e., assumption (iii) in Theorem 1.3 is satisfied. From this, we see that assumption (ii) in Theorem 1.3 also cannot be dropped.
We wonder if assumption (iii) in Theorem 1.3 could be dropped. While we are not able to come up with an example, we can prove a rigidity result of warped product metric without any assumption on Ricci curvature. To this end, we consider the warped product metric
on
![]() $\mathbb {R}\times S^{n-1}$
, where
$\mathbb {R}\times S^{n-1}$
, where
![]() $f>0$
and
$f>0$
and
![]() $\tilde {g}$
is a metric on
$\tilde {g}$
is a metric on
![]() $S^{n-1}$
. Let
$S^{n-1}$
. Let
![]() $\{e_i\}_{i=1}^n$
be an orthonormal basis with respect to g such that
$\{e_i\}_{i=1}^n$
be an orthonormal basis with respect to g such that
![]() $e_1$
is tangent to
$e_1$
is tangent to
![]() $\mathbb {R}$
. Then the Ricci curvature of g is given by (cf. [Reference Li8, Appendix A])
$\mathbb {R}$
. Then the Ricci curvature of g is given by (cf. [Reference Li8, Appendix A])
 $$ \begin{align} Ric_{1j}=-(n-1)\left((\log f)"+\big((\log f)'\big)^2\right)\delta_{1j} =-\frac{(n-1)f"}{f}\delta_{1j} \end{align} $$
$$ \begin{align} Ric_{1j}=-(n-1)\left((\log f)"+\big((\log f)'\big)^2\right)\delta_{1j} =-\frac{(n-1)f"}{f}\delta_{1j} \end{align} $$
for any
![]() $1\leq j\leq n$
, and
$1\leq j\leq n$
, and
 $$ \begin{align} \nonumber Ric_{ij}&=\frac{1}{f^2}\widetilde{Ric}_{ij}-\left((\log f)"+(n-1)\big((\log f)'\big)^2\right)\delta_{ij} \\ &=\frac{1}{f^2}\left[\widetilde{Ric}_{ij}-\big(ff"+(n-2)(f')^2\big)\delta_{ij}\right] \end{align} $$
$$ \begin{align} \nonumber Ric_{ij}&=\frac{1}{f^2}\widetilde{Ric}_{ij}-\left((\log f)"+(n-1)\big((\log f)'\big)^2\right)\delta_{ij} \\ &=\frac{1}{f^2}\left[\widetilde{Ric}_{ij}-\big(ff"+(n-2)(f')^2\big)\delta_{ij}\right] \end{align} $$
for any
![]() $2\leq i, j\leq n$
, where
$2\leq i, j\leq n$
, where
![]() $\widetilde {Ric}$
denotes the Ricci curvature of
$\widetilde {Ric}$
denotes the Ricci curvature of
![]() $\tilde {g}$
. Take f to be a smooth periodic function on
$\tilde {g}$
. Take f to be a smooth periodic function on
![]() $\mathbb {R}$
with period
$\mathbb {R}$
with period
![]() $1$
. Then the warped product metric g defined in (3.5) descends to the metric
$1$
. Then the warped product metric g defined in (3.5) descends to the metric
![]() $ds^2+f(s)^2\tilde {g}$
on
$ds^2+f(s)^2\tilde {g}$
on
![]() $S^1\times S^{n-1}$
, which we still denote by g. And, (3.6) and (3.7) can still be applied. Using (3.6) and (3.7), we can compute the scalar curvature of g:
$S^1\times S^{n-1}$
, which we still denote by g. And, (3.6) and (3.7) can still be applied. Using (3.6) and (3.7), we can compute the scalar curvature of g:
where
![]() $R_{\tilde {g}}$
is the scalar curvature of
$R_{\tilde {g}}$
is the scalar curvature of
![]() $\tilde {g}$
.
$\tilde {g}$
.
Since f is a smooth periodic function on
![]() $\mathbb {R}$
, f is bounded. Let
$\mathbb {R}$
, f is bounded. Let
![]() $m=\min f$
. If
$m=\min f$
. If
![]() $g\geq g_1$
, then it follows from (3.5) that
$g\geq g_1$
, then it follows from (3.5) that
which gives
for all
![]() $s\in \mathbb {R}$
. Take
$s\in \mathbb {R}$
. Take
![]() $s_0\in \mathbb {R}$
with
$s_0\in \mathbb {R}$
with
![]() $f(s_0)=m$
. Then (3.9) with
$f(s_0)=m$
. Then (3.9) with
![]() $s=s_0$
implies that
$s=s_0$
implies that
On the other hand, if
![]() $R_g\geq (n-1)(n-2)$
, then it follows from (3.8) that
$R_g\geq (n-1)(n-2)$
, then it follows from (3.8) that
for all
![]() $s\in \mathbb {R}$
. Once again, if we take
$s\in \mathbb {R}$
. Once again, if we take
![]() $s_0\in \mathbb {R}$
with
$s_0\in \mathbb {R}$
with
![]() $f(s_0)=m=\min f$
, then the second derivative implies that
$f(s_0)=m=\min f$
, then the second derivative implies that
![]() $f"(s_0)\geq 0$
. This together with (3.11) at
$f"(s_0)\geq 0$
. This together with (3.11) at
![]() $s=s_0$
implies that
$s=s_0$
implies that
Hence, it follows from (3.10) and (3.12) that the rescaling metric
![]() $m^{2}\tilde {g}$
on
$m^{2}\tilde {g}$
on
![]() $S^{n-1}$
satisfies
$S^{n-1}$
satisfies
We can then apply Llarull’s result in Theorem 1.1 to infer that
![]() $m^2\tilde {g}=g_{S^{n-1}}$
. To conclude, we have proved the following:
$m^2\tilde {g}=g_{S^{n-1}}$
. To conclude, we have proved the following:
Theorem 3.1 If g is a warped product metric on
![]() $S^1\times S^{n-1}$
given by (3.5) such that
$S^1\times S^{n-1}$
given by (3.5) such that
![]() $g\geq g_1=ds^2+g_{S^{n-1}}$
and
$g\geq g_1=ds^2+g_{S^{n-1}}$
and
![]() $R_g\geq (n-1)(n-2)$
, then
$R_g\geq (n-1)(n-2)$
, then
![]() $g=ds^2+m^{-2}g_{S^{n-1}}$
for some
$g=ds^2+m^{-2}g_{S^{n-1}}$
for some
![]() $m>0$
.
$m>0$
.
Acknowledgments
This work first started when the author was invited by Prof. Jaigyoung Choe to visit the Korea Institute for Advanced Study (KIAS) in the fall of 2022. The author would like to thank Prof. Jaigyoung Choe for raising the question about rigidity, and for the hospitality of KIAS.