Published online by Cambridge University Press: 20 November 2018
Let A be a ring and s2(A) the set of idempotents in A. It is a familiar fact that s2(A) becomes a ring if we define 0, 1 and multiplication as in A, and a new negative and new addition by
1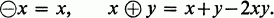
R. A. Melter [3] made the surprising observation that s3(A), where in general sq(A)={x∈A:xq=x}, is a ring if 2 is a unit in A and we define 0,1 minus and multiplication as in A, and a new addition by
2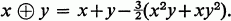
The nonobvious facts are that s3(A) is closed under ⊕ and that ⊕ is associative when applied to the elements of s3(A). The ⊕ in (1) is actually a formal group over A, and so is associative when applied to any elements of A. However in (2) (and similarly in other cases we shall define) the ⊕ is not a formal group, and the associative law depends on the fact that the elements involved are in s3(A).