Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T21:13:42.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Semiclassical Limits of Eigenfunctions on Flat n-Dimensional Tori

Published online by Cambridge University Press:  20 November 2018

Tayeb Aϊssiou
Tayeb Aϊssiou*
Affiliation:
Department of Mathematics, McGill University, Montréal, QC e-mail: aissiou@math.mcgill.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We provide a proof of a conjecture by Jakobson, Nadirashvili, and Toth stating that on an $n$-dimensional flat torus 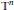${{\mathbb{T}}^{n}}$, and the Fourier transform of squares of the eigenfunctions 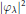${{\left| \varphi \lambda \right|}^{2}}$ of the Laplacian have uniform 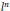${{l}^{n}}$ bounds that do not depend on the eigenvalue 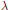$\lambda $. The proof is a generalization of an argument by Jakobson, et al. for the lower dimensional cases. These results imply uniform bounds for semiclassical limits on 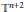${{\mathbb{T}}^{n+2}}$. We also prove a geometric lemma that bounds the number of codimension-one simplices satisfying a certain restriction on an $n$-dimensional sphere 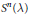${{S}^{n}}\,\left( \text{ }\!\!\lambda\!\!\text{ } \right)$ of radius 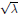$\sqrt{\lambda }$, and we use it in the proof.

Keywords

58G2581Q5035P2042B05semiclassical limitseigenfunctions of Laplacian on a torusquantum limits
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 1 , 01 March 2013 , pp. 3 - 12
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Avakumović, V.. Über die Eigenfunktionen auf geschlossenen Riemannschen Mannigfaltigkeiten. Math. Z. 65 (1956), 327–344. http://dx.doi.org/10.1007/BF01473886 Google Scholar
[2] Aϊssiou, T., Semiclassical limits of eigenforms and eigenfunctions on n-dimensional Tori. M.Sc. Thesis. McGill University, Montreal, QC, 2009.Google Scholar
[3] Bourgain, J, Eigenfunction bounds for the Laplacian on the n-torus. Internat. Math. Res. Notices 1993, no. 3, 61–66.Google Scholar
[4] Bourgain, J and Rudnick, Z, Restrictions of toral eigenfunctions to hypersurfaces. C. R. Math. Acad. Sci. Paris, 347(2009), no. 21-22, 1249–1253.Google Scholar
[5] Bourgain, J and Rudnick, Z, On the nodal sets of toral eigenfunctions. To appear in Invent. Math. ArXiv:1003.1743.Google Scholar
[6] Connes, B, Sur les coefficients des séries trigonométriques convergents sphériquement. C. R. Acad. Sci. Paris Sér. A-B 283(1976), no. 4, 159–161.Google Scholar
[7] Duistermaat, J. J. and Guillemin, V.W., The spectrum of positive elliptic operators and periodic bicharacteristics. Invent. Math. 29 (1975), no. 1, 39–79. http://dx.doi.org/10.1007/BF01405172 Google Scholar
[8] Hörmander, L., The analysis of linear partial differential operators. IV. Springer-Verlag Berlin Heidelberg, 1985.Google Scholar
[9] Hörmander, L., The spectral function of an elliptic operator. Acta. Math. 121 (1968), 193–218, http://dx.doi.org/10.1007/BF02391913 Google Scholar
[10] Jakobson, D., Quantum limits on flat tori. Ann. of Math. 145 (1997), no. 2, 235–266. http://dx.doi.org/10.2307/2951815 Google Scholar
[11] Jakobson, D, Nadirashvili, N, and Toth, J., Geometric properties of eigenfunctions. Russian Math. Surveys 56(2001), no. 6, 1085–1106.Google Scholar
[12] Levitan, B. M. On the asymptotic behavior of the spectral function of a self-adjoint differential equation of the second order. Izvvestiya Akad. Nauk SSSR Ser. Mat. 16 (1952), 325–352 Google Scholar
[13] Mockenhaupt, G. Bounds in Lebesgue spaces of oscillatory integral operators. Habilitationsschrift, Univ. Siegen, Siegen 1996.Google Scholar
[14] Safarov, Y, Asymptotics of the spectrum of a pseudodifferential operator with periodic bicharacteristics. J. Soviet Math. 40 (1988), no. 5, 645–652.Google Scholar
[15] Safarov, Y, Asymptotic of the spectral function of a positive elliptic operator without the nontrap condition. Funct. Anal. App. 22 (1988), no. 3, 213–223. http://dx.doi.org/10.1007/BF01077725 Google Scholar
[16] Safarov, Y and Vassiliev, D, The asymptotic distribution of eigenvalues of partial differential operators. Translations of Mathematical Monographs 155. American Mathematical Society, Providence, RI, 1997.Google Scholar
[17] Sogge, C. Concerning the Lp norm of spectral clusters for second-order elliptic operators on compact anifolds. J. Funct. Anal. 77 (1988), 123–138. http://dx.doi.org/10.1016/0022-1236(88)90081-X Google Scholar
[18] Sogge, C, Toth, J, and Zelditch, S., About the blowup of quasimodes on Riemannian manifolds. J. Geom. Anal. 21 (2011), no. 1, 150–173. http://dx.doi.org/10.1007/s12220-010-9168-6 Google Scholar
[19] Sogge, C. and Zelditch, S., Riemannian manifolds with maximal eigenfunction growth. Duke Math. J. 114 (2002), no. 3, 387–437. http://dx.doi.org/10.1215/S0012-7094-02-11431-8 Google Scholar
[20] Toth, J. and Zelditch, S., Riemannian manifolds with uniformly bounded eigenfunctions. Duke Math. J. 111 (2002), no. 1, 97–132. http://dx.doi.org/10.1215/S0012-7094-02-11113-2 Google Scholar
[21] Zygmund, A., On Fourier coefficients and transforms of functions of two variables. Studia Math. 50 (1974), 189–201.Google Scholar