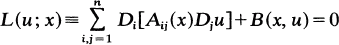Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kusano, Takaŝi
and
Naito, Manabu
1982.
Oscillation Criteria for a Class of Perturbed Schrödinger Equations.
Canadian Mathematical Bulletin,
Vol. 25,
Issue. 1,
p.
71.
Swanson, C. A.
1982.
Bounded Positive Solutions of Semilinear Schrödinger Equations.
SIAM Journal on Mathematical Analysis,
Vol. 13,
Issue. 1,
p.
40.
Yoshida, Norio
1983.
Oscillation Properties of Solutions of Second Order Elliptic Equations.
SIAM Journal on Mathematical Analysis,
Vol. 14,
Issue. 4,
p.
709.
Yoshida, Norio
1984.
An oscillation theorem for sublinear elliptic differential inequalities.
Bulletin of the Australian Mathematical Society,
Vol. 30,
Issue. 3,
p.
387.
Swanson, Charles A.
1985.
Positive solutions of.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 9,
Issue. 12,
p.
1319.
Furusho, Yasuhiro
1985.
Positive solutions of linear and quasilinear elliptic equations in unbounded domains.
Hiroshima Mathematical Journal,
Vol. 15,
Issue. 1,
Usami, Hiroyuki
1995.
Nonexistence of positive solutions and oscillation criteria for second-order semilinear elliptic inequalities.
Archive for Rational Mechanics and Analysis,
Vol. 130,
Issue. 3,
p.
277.
Mařík, Robert
2000.
Oscillation Criteria for PDE with p-Laplacian via the Riccati Technique.
Journal of Mathematical Analysis and Applications,
Vol. 248,
Issue. 1,
p.
290.
Naito, Yūki
and
Usami, Hiroyuki
2001.
Oscillation criteria for quasilinear elliptic equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 46,
Issue. 5,
p.
629.
Xu, Zhiting
Jia, Baoguo
and
Ma, Dongkui
2004.
Oscillation theorems for elliptic equations with damping.
Applied Mathematics and Computation,
Vol. 156,
Issue. 1,
p.
93.
Xu, Zhiting
and
Xia, Yong
2006.
Oscillation of Second Order Damped Elliptic Equations via Weighted Averages Technique.
Rocky Mountain Journal of Mathematics,
Vol. 36,
Issue. 6,
Xu, Zhi-Ting
2006.
Oscillation of second-order elliptic equations with damping terms.
Journal of Mathematical Analysis and Applications,
Vol. 317,
Issue. 1,
p.
349.
Xu, Zhiting
2006.
On the oscillation of second order quasilinear elliptic equations.
Mathematical and Computer Modelling,
Vol. 43,
Issue. 1-2,
p.
30.
Zhuang, Rong-Kun
Wang, Qi-Ru
and
Yao, Zheng-An
2007.
Some new oscillation theorems for second order nonlinear elliptic equations with damping.
Journal of Mathematical Analysis and Applications,
Vol. 330,
Issue. 1,
p.
622.
Xu, Zhi-ting
2007.
Oscillation Theorems for Nonlinear Second Order Elliptic Equations.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 23,
Issue. 4,
p.
569.
Xu, Zhi Ting
2007.
Oscillation Theorems for Quasilinear Elliptic Differential Equations.
Acta Mathematica Sinica, English Series,
Vol. 23,
Issue. 7,
p.
1189.
Zhuang, Rong-Kun
2008.
Annual oscillation criteria for second-order nonlinear elliptic differential equations.
Journal of Computational and Applied Mathematics,
Vol. 217,
Issue. 1,
p.
268.
Xu, Zhiting
2008.
Oscillation of second order damped elliptic differential equations.
Mathematical and Computer Modelling,
Vol. 47,
Issue. 3-4,
p.
341.
XU, ZHITING
2008.
OSCILLATION CRITERIA FOR CERTAIN DAMPED PDE'S WITH p-LAPLACIAN.
Glasgow Mathematical Journal,
Vol. 50,
Issue. 1,
p.
129.
Xu, Zhi Ting
2008.
Averaging technique for the oscillation of second order damped elliptic equations.
Acta Mathematica Sinica, English Series,
Vol. 24,
Issue. 5,
p.
829.