Published online by Cambridge University Press: 20 November 2018
The generalized orthogonal matching pursuit 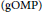 $\left( \text{gOMP} \right)$ algorithm has received much attention in recent years as a natural extension of the orthogonal matching pursuit
$\left( \text{gOMP} \right)$ algorithm has received much attention in recent years as a natural extension of the orthogonal matching pursuit 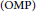 $\left( \text{OMP} \right)$. It is used to recover sparse signals in compressive sensing. In this paper, a new bound is obtained for the exact reconstruction of every
$\left( \text{OMP} \right)$. It is used to recover sparse signals in compressive sensing. In this paper, a new bound is obtained for the exact reconstruction of every  $K$-sparse signal via the
$K$-sparse signal via the 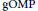 $\text{gOMP}$ algorithm in the noiseless case. That is, if the restricted isometry constant
$\text{gOMP}$ algorithm in the noiseless case. That is, if the restricted isometry constant 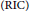 $\left( \text{RIC} \right)$
$\left( \text{RIC} \right)$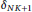 ${{\delta }_{NK+1}}$ of the sensing matrix
${{\delta }_{NK+1}}$ of the sensing matrix  $A$ satisfies
$A$ satisfies
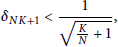 ${{\delta }_{NK+1}}\,<\frac{1}{\sqrt{\frac{K}{N}+\,1}},$
${{\delta }_{NK+1}}\,<\frac{1}{\sqrt{\frac{K}{N}+\,1}},$
then the 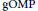 $\text{gOMP}$ can perfectly recover every
$\text{gOMP}$ can perfectly recover every  $K$-sparse signal
$K$-sparse signal  $x$ from
$x$ from 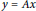 $y\,=\,Ax$. Furthermore, the bound is proved to be sharp. In the noisy case, the above bound on
$y\,=\,Ax$. Furthermore, the bound is proved to be sharp. In the noisy case, the above bound on 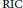 $\text{RIC}$ combining with an extra condition on the minimum magnitude of the nonzero components of
$\text{RIC}$ combining with an extra condition on the minimum magnitude of the nonzero components of  $K$-sparse signals can guarantee that the
$K$-sparse signals can guarantee that the 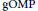 $\text{gOMP}$ selects all of the support indices of the
$\text{gOMP}$ selects all of the support indices of the  $K$-sparse signals.
$K$-sparse signals.