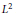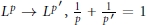Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shayya, Bassam
2009.
Affine restriction for radial surfaces.
Mathematische Zeitschrift,
Vol. 262,
Issue. 1,
p.
41.
Iosevich, Alex
and
Roudenko, Svetlana
2010.
Additive Number Theory.
p.
171.
Oberlin, Daniel
2011.
A uniform Fourier restriction theorem for surfaces in ℝ^{𝕕}.
Proceedings of the American Mathematical Society,
Vol. 140,
Issue. 1,
p.
263.
Hickman, Jonathan
2014.
AN AFFINE FOURIER RESTRICTION THEOREM FOR CONICAL SURFACES.
Mathematika,
Vol. 60,
Issue. 2,
p.
374.