Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T06:29:56.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Similarity and Coincidence Isometries for Modules

Published online by Cambridge University Press:  20 November 2018

Svenja Glied
Svenja Glied*
Affiliation:
Fakultät für Mathematik, Universität Bielefeld, Postfach 100131, 33501 Bielefeld, GermanyURL: http://www.math.uni-bielefeld.de/baake/ e-mail: sglied@math.uni-bielefeld.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The groups of (linear) similarity and coincidence isometries of certain modules $\Gamma $ in $d$-dimensional Euclidean space, which naturally occur in quasicrystallography, are considered. It is shown that the structure of the factor group of similarity modulo coincidence isometries is the direct sum of cyclic groups of prime power orders that divide $d$. 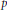In particular, if the dimension $d$ is a prime number $p$, the factor group is an elementary abelian 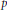$p$-group. This generalizes previous results obtained for lattices to situations relevant in quasicrystallography.

Keywords

20H1582D2552C23
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 1 , 01 March 2012 , pp. 98 - 107
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Adkins, W. A. and Weintraub, S. H., Algebra. An Approach via Module Theory. Corr. 2nd printing, Springer, New York, 1999.Google Scholar
[2] Baake, M., Solution of the coincidence problem in dimensions d ≤ 4. In: The mathematics of long-range aperiodic order (Waterloo, ON, 1995) NATO Adv. Sci. Inst. Ser. C 489, Kluwer Acad. Publ., Dordrecht, 1997, 9–44.Google Scholar
[3] Baake, M. and Grimm, U., A note on shelling. Discrete Comput. Geom. 30(2003), 573–589.Google Scholar
[4] Baake, M. and Grimm, U., Bravais colourings of planar modules with N-fold symmetry. Z. Krist. 219(2004), 72–80. doi:10.1524/zkri.219.2.72.26322Google Scholar
[5] Baake, M. and Grimm, U., Combinatorial problems of (quasi)crystallography. In: Quasicrystals: Structure and Physical Properties (ed. Trebin, H.-R.), Wiley-VCH, Weinheim, 2003, 160–171.Google Scholar
[6] Baake, M., Grimm, U., Heuer, M. and Zeiner, P., Coincidence rotations of the root lattice A 4 . European J. Combin. 29(2008), 1808–1819. doi:10.1016/j.ejc.2008.01.012Google Scholar
[7] Baake, M. and Moody, R. V., Multi-component model sets and invariant densities. In: Aperiodic 97 (eds.de Boissieu, M., Verger-Gaugry, J.-L. and Currat, R.), World Scientific, Singapore, 1998, 9–20; math-ph/9809005.Google Scholar
[8] Baake, M. and Moody, R. V., Similarity submodules and root systems in four dimensions. Canad. J. Math. 51(1999), 1258–1276. doi:10.4153/CJM-1999-057-0Google Scholar
[9] Baake, M., Pleasants, P. A. B. and Rehmann, U., Coincidence site modules in 3-space. Discrete Comput. Geom. 38(2007), 111–138. doi:10.1007/s00454-007-1327-6Google Scholar
[10] Baake, M., Pleasants, P. A. B. and Roth, J., Planar coincidences for N-fold symmetry. J. Math. Phys. 37(1996), 1029–1058. doi:10.1063/1.531424Google Scholar
[11] Baake, M., Scharlau, R., and Zeiner, P., Similar sublattices of planar lattices. Canad. J. Math., to appear. doi:10.4153/CJM-2011-019-9Google Scholar
[12] Borevich, Z. I. and Shafarevich, I. R., Number Theory. Academic Press, New York, 1966.Google Scholar
[13] Conway, J. H., Rains, E. M. and Sloane, N. J. A., On the existence of similar sublattices. Canad. J. Math. 51(1999), 1300–1306. doi:10.4153/CJM-1999-059-5Google Scholar
[14] Glied, S. and Baake, M., Similarity versus coincidence rotations of lattices. Z. Krist. 223(2008), Issue 11–12, ICQ10 Proceedings Part I. Preprint: arXiv:0808.0109 [math.MG].Google Scholar
[15] Huck, C., A note on coincidence isometries of modules in Euclidean space. Z. Krist. 224(2009), no. 7, 341–344. doi:10.1524/zkri.2009.1148Google Scholar
[16] Huck, C., Discrete Tomography of Delone Sets with Long Range Order. PhD thesis (Univ. Bielefeld), Logos Verlag, Berlin, 2007.Google Scholar
[17] Pleasants, P. A. B., Designer quasicrystals: Cut-and-project sets with pre-assigned properties. In: Directions in Mathematical Quasicrystals, CRM Monogr. Ser. 13, Amer. Math. Soc., Providence, RI, 2000, 95–141.Google Scholar
[18] Scott, W. R., Group Theory. Prentice-Hall, Englewood Cliffs, 1964.Google Scholar
[19] Washington, L. C., Introduction to Cyclotomic Fields. 2nd edition, Springer, New York, 1997.Google Scholar
[20] Zou, Y. M., Structures of coincidence symmetry groups. Acta Cryst. A 62(2006), 109–114.Google Scholar