Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T05:36:33.540Z Has data issue: false hasContentIssue false
  • English
  • Français

Simplicial Cohomology of Some Semigroup Algebras

Published online by Cambridge University Press:  20 November 2018

F. Gourdeau ,
A. Pourabbas  and
M. C. White
F. Gourdeau
Affiliation:
Département de Mathématiques et de Statistique, Université Laval, Cité Universitaire, QC e-mail: Frederic.Gourdeau@mat.ulaval.ca
A. Pourabbas
Affiliation:
Faculty of Mathematics and Computer Science, Amirkabir University of Technology, 424 Hafez Avenue, Tehran 15914, Iran e-mail: arpabbas@aut.ac.ir
M. C. White
Affiliation:
Department of Mathematics, University of Newcastle, Newcastle upon Tyne, NE1 7RU, England e-mail: Michael.White@ncl.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we investigate the higher simplicial cohomology groups of the convolution algebra 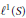${{\ell }^{1}}\left( S \right)$ for various semigroups 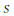$S$. The classes of semigroups considered are semilattices, Clifford semigroups, regular Rees semigroups and the additive semigroups of integers greater than $a$ for some integer $a$. Our results are of two types: in some cases, we show that some cohomology groups are 0, while in some other cases, we show that some cohomology groups are Banach spaces.

Keywords

43A2046M2016E40simplicial cohomologysemigroup algebra
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 1 , 01 March 2007 , pp. 56 - 70
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Bonsall, F. F. and Duncan, J., Complete Normed Algebras. Ergebnisse der Mathematik und ihrer Grenzgebiete 80, Springer-Verlag, New York, 1973.10.1007/978-3-642-65669-9Google Scholar
[2] Bowling, S. and Duncan, J., First order cohomology of Banach semigroup algebras. Semigroup Forum 56(1998), no. 1, 130–145.10.1007/s00233-002-7009-zGoogle Scholar
[3] Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups. Mathematical Surveys 7, American Mathematical Society, Providence, RI, 1961.Google Scholar
[4] Dales, H. G. and Duncan, J., Second order cohomology in groups of some semigroup algebras. In: Banach Algebras,Walter de Gruyter, Berlin, 1998, pp. 101–117.Google Scholar
[5] Gourdeau, F., Johnson, B. E. and White, M. C., The cyclic and simplicial cohomology of ℓ 1(ℕ). Trans. Amer. Math. Soc. 357(2005), no. 12, 5097–5113.10.1090/S0002-9947-05-03702-5Google Scholar
[6] Gourdeau, F., Lykova, Z. A. and White, M. C., A Künneth formula in topological homology and its applications to the simplicial cohomology of . Studia Math. 166(2005), no. 1, 29–54.10.4064/sm166-1-3Google Scholar
[7] Gourdeau, F., Lykova, Z. A. and White, M. C., The simplicial cohomology of . In: Banach Algebras and Their Applications, Contemp. Math. 363, American Mathematical Society, Providence, RI, 2004, pp. 95–109.10.1090/conm/363/06645Google Scholar
[8] Hewitt, E. and Ross, K. A., Abstract Harmonic Analysis. Vol. I. Structure of Topological Groups, Integration Theory, Group Representations. Second edition. Grundlehren der Mathematischen Wissenschaften 115, Springer-Verlag, Berlin, 1979.Google Scholar
[9] Helemskii, A. Ya., Banach cyclic (co)homology and the Connes-Tzygan exact sequence. J. London Math. Soc. 46(1992), no. 3, 449–462.10.1112/jlms/s2-46.3.449Google Scholar
[10] Howie, J. M., Fundamentals of Semigroup Theory. London Mathematical Society Monographs 12. The Clarendon Press, New York, 1995.Google Scholar
[11] Johnson, B. E., Cohomology in Banach Algebras. Memoirs of the American Mathematical Society 127, American Mathematical Society, Providence, RI, 1972.10.1090/memo/0127Google Scholar
[12] Pourabbas, A., Second cohomology group of group algebras with coefficients in iterated duals. Proc. Amer.Math. Soc. 132(2004), no. 5, 1403–1410.Google Scholar