Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T15:52:09.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Smooth Approximation of Lipschitz Projections

Published online by Cambridge University Press:  20 November 2018

Hanfeng Li
Hanfeng Li*
Affiliation:
Department of Mathematics, SUNY at Buffalo, Buffalo, NY 14260-2900, USAe-mail: hfli@math.buffalo.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that any Lipschitz projection-valued function 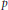$p$ on a connected closed Riemannian manifold can be approximated uniformly by smooth projection-valued functions $q$ with Lipschitz constant close to that of 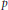$p$. This answers a question of Rieffel.

Keywords

19K14approximationLipschitz constantprojection
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 4 , 01 December 2012 , pp. 762 - 766
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Greene, R. E. and Wu, H., On the subharmonicity and plurisubharmonicity of geodesically convex functions. Indiana Univ. Math. J. 22(1972/73), 641–653. http://dx.doi.org/10.1512/iumj.1973.22.22052 Google Scholar
[2] Greene, R. E. and Wu, H., Integrals of subharmonic functions on manifolds of nonnegative curvature. Invent. Math. 27(1974), 265–298. http://dx.doi.org/10.1007/BF01425500 Google Scholar
[3] Greene, R. E. and Wu, H., C ∞ approximations of convex, subharmonic, and plurisubharmonic functions. Ann. Sci. é cole Norm. Sup. 12(1979), no. 1, 47–84.Google Scholar
[4] Rieffel, M. A., Gromov-Hausdorff distance for quantum metric spaces. Mem. Amer. Math. Soc. 168(2004), no. 796, 1–65.Google Scholar
[5] Rieffel, M. A., Vector bundles and Gromov-Hausdorff distance. J. K-Theory 5(2010), no. 1, 39–103. http://dx.doi.org/10.1017/is008008014jkt080 Google Scholar