Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-30T22:36:52.869Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Admissible Estimators in Extreme Value Densities

Published online by Cambridge University Press:  20 November 2018

R. Singh
R. Singh*
Affiliation:
Department of MathematicsUniversity of Saskatchewan Saskatoon, Saskatchewan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be a random variable having the extreme value density of the form

(1)

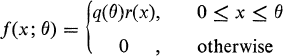
where r is assumed to be a positive Lebesgue measurable function of x and the function q is defined by

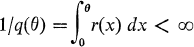
for all θ in Ω = (0, ∞). It is further assumed that q(θ) approaches zero as θ → ∞.

In this note we are concerned with estimating parametric functions g(θ) of the form [1/q(θ)]α, α any real number. The loss function is assumed to be squared error and the estimators are assumed to be functions of a single observation X.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 1 , April 1975 , pp. 105 - 110
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Blyth, C. R., On minimax statistical decision procedures and their admissibility, Ann. Math. Statist. 22 (1951) pp. 22-42.Google Scholar
2. Blyth, C. R. and Roberts, D. M., On inequalities of Cramer-Rao type and admissibility proofs, Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, 1 (1972) pp. 17-30.Google Scholar
3. Girshick, M. A. and Savage, L. J., Bayes and minimax estimates for quadratic loss functions, Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, 1 (1958) pp. 53-73.Google Scholar
4. Hodges, J. L. and Lehmann, E.L., Some applications of the Cramer-Rao inequality, Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, 1 (1951) pp. 13-22.Google Scholar
5. Karlin, S., Admissibility for estimation with quadratic loss, Ann. Math. Statist. 29 (1958) pp. 406-436.Google Scholar
6. Singh, R., Admissible estimators of θr in some extreme value densities, Can. Math. Bull. 14 (1971) pp. 411-414.Google Scholar