Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Burdzy, Krzysztof
1986.
Brownian excursions and minimal thinness.
Mathematische Zeitschrift,
Vol. 192,
Issue. 1,
p.
89.
Burdzy, Krzysztof
1990.
Minimal fine derivatives and Brownian excursions.
Nagoya Mathematical Journal,
Vol. 119,
Issue. ,
p.
115.
Betsakos, Dimitrios
2014.
On the images of horodisks under holomorphic self-maps of the unit disk.
Archiv der Mathematik,
Vol. 102,
Issue. 1,
p.
91.


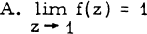 , where
, where 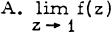 denotes the (outer) angular limit of f (z) at z = 1. Let us now define
denotes the (outer) angular limit of f (z) at z = 1. Let us now define 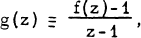 and then focus our attention on the behaviour of g(z) in an arbitrary angular neighbourhood of z = 1. Whenever
and then focus our attention on the behaviour of g(z) in an arbitrary angular neighbourhood of z = 1. Whenever  exists, this limit is commonly referred to as the angular derivative of f(z) at z = 1.
exists, this limit is commonly referred to as the angular derivative of f(z) at z = 1.