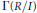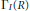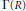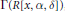Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tamizh Chelvam, T.
Asir, T.
and
Selvakumar, K.
2016.
Algebra and its Applications.
Vol. 174,
Issue. ,
p.
363.
Nikandish, R.
Nikmehr, M. J.
and
Bakhtyiari, M.
2016.
Coloring of the annihilator graph of a commutative ring.
Journal of Algebra and Its Applications,
Vol. 15,
Issue. 07,
p.
1650124.
Shaveisi, Farzad
2016.
Some Results on Annihilating-ideal Graphs.
Canadian Mathematical Bulletin,
Vol. 59,
Issue. 3,
p.
641.
Hashemi, Ebrahim
Abdi, Mona
Alhevaz, Abdollah
and
Su, Huadong
2020.
Domination number of graphs associated with rings.
Journal of Algebra and Its Applications,
Vol. 19,
Issue. 01,
p.
2050009.