Article contents
Some Rings of Invariants that are Cohen-Macaulay
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 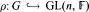 be a representation of the finite group G over the field
be a representation of the finite group G over the field  . If the order |G| of G is relatively prime to the characteristic of
. If the order |G| of G is relatively prime to the characteristic of  or n = 1 or 2, then it is known that the ring of invariants
or n = 1 or 2, then it is known that the ring of invariants 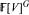 is Cohen-Macaulay. There are examples to show that
is Cohen-Macaulay. There are examples to show that 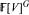 need not be Cohen-Macaulay when |G| is divisible by the characteristic of
need not be Cohen-Macaulay when |G| is divisible by the characteristic of  . In all such examples
. In all such examples 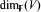 is at least 4. In this note we fill the gap between these results and show that rings of invariants in three variables are always Cohen-Macaulay.
is at least 4. In this note we fill the gap between these results and show that rings of invariants in three variables are always Cohen-Macaulay.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1996
References
- 9
- Cited by


