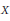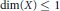Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rustad, Alf B.
2002.
Quasi-measures with image transformations as generalized variables.
Journal of Mathematical Analysis and Applications,
Vol. 271,
Issue. 1,
p.
16.
Aarnes, J. F.
and
Butler, S. V.
2003.
Super-measures and finitely defined topological measures.
Acta Mathematica Hungarica,
Vol. 99,
Issue. 1-2,
p.
33.
Aarnes, Johan F.
and
Grubb, D.J.
2004.
Quasi-measures and image transformations on completely regular spaces.
Topology and its Applications,
Vol. 135,
Issue. 1-3,
p.
33.
Grubb, D.J.
and
Laberge, Tim
2008.
Smoothness Properties of Quasi-Measures.
Rocky Mountain Journal of Mathematics,
Vol. 38,
Issue. 2,
MONZNER, ALEXANDRA
and
ZAPOLSKY, FROL
2011.
A COMPARISON OF SYMPLECTIC HOMOGENIZATION AND CALABI QUASI-STATES.
Journal of Topology and Analysis,
Vol. 03,
Issue. 03,
p.
243.
Zapolsky, Frol
2012.
Isotopy-invariant topological measures on closed orientable surfaces of higher genus.
Mathematische Zeitschrift,
Vol. 270,
Issue. 1-2,
p.
133.
Svistula, M.
2018.
Decomposition of transformations.
Acta Mathematica Hungarica,
Vol. 155,
Issue. 2,
p.
376.
Butler, Svetlana V.
2022.
Weak Convergence of Topological Measures.
Journal of Theoretical Probability,
Vol. 35,
Issue. 3,
p.
1614.