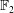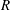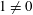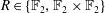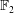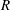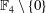Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
LaGrange, John D.
2024.
Eigenvalues of zero-divisor graphs, Catalan numbers, and a decomposition of eigenspaces.
Linear and Multilinear Algebra,
Vol. 72,
Issue. 14,
p.
2329.