Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T16:22:34.551Z Has data issue: false hasContentIssue false
  • English
  • Français

A Spectral Identity on Jacobi Polynomials and its Analytic Implications

Published online by Cambridge University Press:  20 November 2018

Richard Awonusika  and
Ali Taheri
Richard Awonusika
Affiliation:
Department of Mathematics, University of Sussex, Brighton, UK, e-mail : r.awonusika@sussex.ac.uk, a.taheri@sussex.ac.uk
Ali Taheri
Affiliation:
Department of Mathematics, University of Sussex, Brighton, UK, e-mail : r.awonusika@sussex.ac.uk, a.taheri@sussex.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Jacobi coefficients 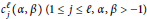$c_{j}^{\ell }\left( \alpha ,\,\beta \right)\,\left( 1\,\le \,j\,\le \,\ell ,\,\alpha ,\,\beta \,>\,-1 \right)$ are linked to the Maclaurin spectral expansion of the Schwartz kernel of functions of the Laplacian on a compact rank one symmetric space. It is proved that these coefficients can be computed by transforming the even derivatives of the Jacobi polynomials 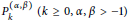$P_{k}^{\left( \alpha ,\,\beta \right)}\,\left( k\,\ge \,0,\,\alpha ,\,\beta \,>\,-1 \right)$ into a spectral sum associated with the Jacobi operator. The first few coefficients are explicitly computed, and a direct trace interpretation of the Maclaurin coefficients is presented.

Keywords

33C0533C4535A0835C0535C1035C15Jacobi coefficientLaplace–Beltrami operatorsymmetric spaceMaclaurin expansionJacobi polynomial
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 3 , 01 September 2018 , pp. 473 - 482
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Awonusikaand, R. O. Taheri, A., On Jacobi polynomials and Maclaurin spectral functions on rank one Symmetrie Spaces, J. Analysis 25(2017), no. 1, 139–166. http://dx.doi.Org/10.1007/s41478-017-0038-5Google Scholar
[2] Bakry, D., Gentil, I., and Ledoux, M., Analysis and geometry of Markov diffusion Operators. Grundlehren der Mathematischen Wissenschaften, 348, Springer, Cham, 2014. http://dx.doi.org/10.1007/978-3-319-00227-9Google Scholar
[3] Berger, M., Gauduchon, P., Mazet, E., Le spectre dune variete Riemannienne, Springer, 1971.Google Scholar
[4] Gradshtejn, I. S., Ryzhik, I. M., Table of Integrals, Series and Products, Academic Press, 2007. http://dx.doi.org/10.1090/S0025-5718-1982-0669666-2Google Scholar
[5] Helgason, S., Eigenspaces of the Laplacian; integral representations and irreducibility. J. Funct. Anal. 17(1974), 328–353. http://dx.doi.org/10.1016/0022-1236(74)90045-7Google Scholar
[6] Helgason, S., Topics in harmonic analysis on homogeneous Spaces. Progress in Mathematics, 13, Birkhäuser, Boston, MA, 1981.Google Scholar
[7] Koornwinder, T. H., The addition formula for Jacobi polynomials: I Summary of results. Indag. Math. 34(1972), 188–191. http://dx.doi.Org/10.1016/1385-7258(72)90011-XGoogle Scholar
[8] Koornwinder, T. H., A newproof of a Paley-Wiener type theorem for the Jacobi transform. Ark. Mat. 13(1975), 145–159. http://dx.doi.org/10.1007/BF02386203Google Scholar
[9] McKean, H. and Singer, I. M., Curvature and the eigenvalues ofthe Laplacian. J. Differential Geometry 1(1967), no. 1, 43–69. http://dx.doi.Org/10.4310/jdg/1214427880Google Scholar
[10] Morris, C. and Taheri, A., On Weyl's asymptotics and remainder termfor the orthogonal and unitary groups. J. Fourier Anal. Appl., to appear.Google Scholar
[11] Osgood, B., Phillips, R., and Sarnak, P., Extremais and determinants of Laplacians. J. Funct. Anal. 80(1988), 148–211. http://dx.doi.org/10.1016/0022-1236(88)90070-5Google Scholar
[12] Sarnak, P., Determinants of Laplacians. Comm. Math. Phys. 110(1987), no. 1, 113–120. http://dx.doi.Org/10.1007/BF01209019Google Scholar
[13] Sarnak, P., Determinants of Laplacians: heights and finiteness. In: Analysis, et cetera, Academic Press, Boston, MA, pp. 601–622.Google Scholar
[14] Seeley, R. T., Complex powers of an elliptic Operator. In: Singular Integrals (Proc. Sympos. Pure Math., Chicago, III, 1966), American Mathematical Society Providence, RI, 1966, pp. 288–307.Google Scholar
[15] Taheri, A., Function Spaces andpartial differential equations. I & II, Oxford Lecture Series in Mathematics and Its Applications, 40 & 41, Oxford University Press, 2015. http://dx.doi.Org/10.1093/acprof:oso/9780198733157.003.0013Google Scholar
[16] Vilenkin, N. J., Special functions and the theory of group representations. Translations of Mathematical Monographs, 22, American Mathematical Society, Providence, RI, 1968.Google Scholar
[17] Warner, G., Harmonic analysis on semisimple Lie groups. Die Grundlehren der mathematischen Wissenschaften, Band 188. Springer-Verlag, New York-Heidelberg, 1972.Google Scholar