Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T00:31:18.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral Properties of a Family of Minimal Tori of Revolution in the Five-dimensional Sphere

Published online by Cambridge University Press:  20 November 2018

Mikhail Karpukhin
Mikhail Karpukhin*
Affiliation:
Department of Geometry and Topology, Faculty of Mechanics and Mathematics, Moscow State University, Leninskie Gory, GSP-1, 119991, Moscow, Russia. e-mail: mikhail.karpukhin@gmail.com Independent University of Moscow, Bolshoy Vlasyevskiy pereulok 11, 11902, Moscow, Russia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

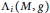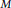The normalized eigenvalues ${{\Lambda }_{i}}\left( M,\,g \right)$ of the Laplace–Beltrami operator can be considered as functionals on the space of all Riemannian metrics $g$ on a fixed surface $M$. In recent papers several explicit examples of extremal metrics were provided. These metrics are induced by minimal immersions of surfaces in 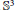${{\mathbb{S}}^{3}}$ or 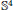${{\mathbb{S}}^{4}}$. In this paper a family of extremal metrics induced by minimal immersions in 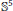${{\mathbb{S}}^{5}}$ is investigated.

Keywords

58J50Extremal metricminimal surface
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 285 - 296
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Bando, S. and Urakawa, H., Generic properties of the eigenvalue of Laplacian for compact Riemannian manifolds. Tôhoku Math. J. 35 (1983), no. 2,155–172. http://dx.doi.Org/10.2748/tmj/1178229047 Google Scholar
[2] Berger, M., Sur les premières valeurs propres des variétés Riemanniennes. Compositio Math. 26 (1973), 129–149.Google Scholar
[3] Byrd, P. and Friedman, M., Handbook of elliptic integrals for engineers and scientists. Second éd., Die Grundlehren der mathematischen Wissenschaften, 67, Springer-Verlag, New York-Heidelberg, 1971.Google Scholar
[4] Coddington, E. A. and Levinson, N., Theory of ordinary differential equations. McGraw-Hill Book Company, Inc., New York-Toronto-London, 1955.Google Scholar
[5] El Soufi, A., Giacomini, H., and Jazar, M., A unique extremal metric for the least eigenvalue of the Laplacian on the Klein bottle. Duke Math. J. 135 (2006), no. 1,181–202. http://dx.doi.Org/10.1215/S0012–7094-06-13514-7 Google Scholar
[6] El Soufi, A. and Ilias, S., Riemannian manifolds admitting isometric immersions by their first eigenfunctions. Pacific. J. Math. 195 (2000), no. 1, 91–99. http://dx.doi.org/10.2140/pjm.2000.195.91 Google Scholar
[7] El Soufi, A. and Ilias, S., Laplacian eigenvalues functionak and metric deformations on compact manifolds. J. Geom. Phys. 58 (2008), no. 1, 89–104. http://dx.doi.Org/10.1016/j.geomphys.2007.09.008 Google Scholar
[8] Erdelyi, A., Magnus, W., Oberhettinger, F., and Tricomi, F., Higher transcendental functions. Vol. III. McGraw-Hill Book Company Inc., New York-Toronto-London, 1955.Google Scholar
[9] Haskins, M., Special Lagrangian cones. Amer. J. Math. 126 (2004), no. 4, 845–871. http://dx.doi.Org/10.1353/ajm.2004.0029 Google Scholar
[10] Henrot, A., Extremum problems for eigenvalues of elliptic operators. Birkhâuser Verlag, Basel, 2006.Google Scholar
[11] Hersch, J., Quatre propriétés isopérimétriques de membranes sphériques homogènes. C. R. Acad. Sci. Paris Sér A-B 270 (1970), A1645-A1648.Google Scholar
[12] Jakobson, D., Nadirashvili, N., and I. Polterovich, Extremal Metric for the First Eigenvalue on a Klein Bottle. Canad. J. Math. 58 (2006), no. 2, 381–400. http://dx.doi.Org/10.4153/CJM-2006-016-0 Google Scholar
[13] Joyce, D., Special Lagrangian m-folds in Cm with symmetries. Duke Math. J. 115 (2002), 1–51. http://dx.doi.Org/10.1215/S0012–7094-02-11511-7 Google Scholar
[14] Karpukhin, M. A., Nonmaximality of extremal metrics on torus and Klein bottle. Sb. Math. 204 (2013), no. 11–12, 1728–1744.Google Scholar
[15] Karpukhin, M. A., Spectral properties of bipolar surfaces to Otsuki tori. J. Spectr. Theory. 4 (2014), no. 1, 87–111. http://dx.doi.Org/10.4171/JST/63 Google Scholar
[16] Kobayashi, S. and Nomizu, K., Foundations of differential geometry. Vol. IL, Interscience Tracts in Pure and Applied Mathematics, 15, vol. II, Interscience Publishers John Wiley & Sons, Inc., New York-London-Sydney, 1969.Google Scholar
[17] Korevaar, N., Upper bounds for eigenvalues of conformai metrics. J. Differential Geom. 37 (1993), no. 1, 79–93.Google Scholar
[18] Lapointe, H., Spectral properties of bipolar minimal surfaces in §4. Differential Geom. Appl. 26 (2008), no. 1, 9–22. http://dx.doi.Org/10.1016/j.difgeo.2007.12.001 Google Scholar
[19] Li, P. and Yau, S.-T., A new conformai invariant and its applications to the Willmore conjecture and the first eigenvalue of compact surfaces. Invent. Math. 69 (1982), no. 2, 269–291. http://dx.doi.org/10.1007/BF01399507 Google Scholar
[20] Mironov, A. E., Finite-gap minimal Lagrangian surfaces in CF2. In: Riemann surfaces, harmonic maps and visualization, OCAMI Studies Series, 3, Osaka Munie. Univ. Press, Osaka, 2010, pp. 185–196.Google Scholar
[21] Mironov, A. E., New examples of Hamiltonian-minimal and minimal Lagrangian submanifolds in C” and CF”. (Russian) Mat. Sb. 195 (2004), no. 1, 89–102; translation in Sb. Math. 195 (2004), no. 1–2, 85–96. http://dx.doi.org/10.4213/sm794 Google Scholar
[22] Nadirashvili, N., Berger's isoperimetric problem and minimal immersions of surfaces. Geom. Funct. Anal. 6 (1996), no. 5, 877–897. http://dx.doi.Org/10.1007/BF02246788 Google Scholar
[23] Nadirashvili, N., Isoperimetric inequality for the second eigenvalue of a sphere. J. Differential Geom. 61 (2002), no. 2, 335–340.Google Scholar
[24] Penskoi, A. V., Extremal spectral properties ofLawson tau-surfaces and theLamé equation. Moscow Math. J. 12 (2012), no. 1,173–192, 216.Google Scholar
[25] Nadirashvili, N., Extremal spectral properties of Otsuki tori. Math. Nachr. 286 (2013), no. 4, 379–391. http://dx.doi.org/10.1002/mana.201200003 Google Scholar
[26] Simons, J., Minimal varieties in Riemannian manifolds. Ann. of Math. 88 (1968), no. 2, 62–105. http://dx.doi.Org/10.2307/1970556 Google Scholar
[27] Volkmer, H., Coexistence of periodic solutions oflnce's equation. Analysis (Munich) 23 (2003), no. 1, 97–105.Google Scholar
[28] Yang, P. C. and Yau, S.-T., Eigenvalues of the Laplacian of compact Riemann surfaces and minimal submanifolds. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 7 (1980), no. 1, 55–63.Google Scholar