Article contents
Spectrality of a class of Moran measures on 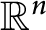 $\mathbb {R}^{n}$ with consecutive digit sets
$\mathbb {R}^{n}$ with consecutive digit sets
Published online by Cambridge University Press: 13 April 2022
Abstract
Let
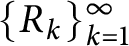 $\{R_{k}\}_{k=1}^{\infty }$
be a sequence of expanding integer matrices in
$\{R_{k}\}_{k=1}^{\infty }$
be a sequence of expanding integer matrices in
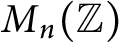 $M_{n}(\mathbb {Z})$
, and let
$M_{n}(\mathbb {Z})$
, and let
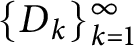 $\{D_{k}\}_{k=1}^{\infty }$
be a sequence of finite digit sets with integer vectors in
$\{D_{k}\}_{k=1}^{\infty }$
be a sequence of finite digit sets with integer vectors in
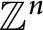 ${\mathbb Z}^{n}$
. In this paper, we prove that under certain conditions in terms of
${\mathbb Z}^{n}$
. In this paper, we prove that under certain conditions in terms of
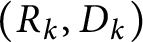 $(R_{k},D_{k})$
for
$(R_{k},D_{k})$
for
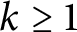 $k\ge 1$
, the Moran measure
$k\ge 1$
, the Moran measure
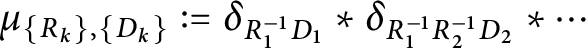 $$ \begin{align*} \mu_{\{R_{k}\},\{D_{k}\}}:=\delta_{R_{1}^{-1}D_{1}}\ast\delta_{R_{1}^{-1}R_{2}^{-1}D_{2}}\ast\cdots \end{align*} $$
$$ \begin{align*} \mu_{\{R_{k}\},\{D_{k}\}}:=\delta_{R_{1}^{-1}D_{1}}\ast\delta_{R_{1}^{-1}R_{2}^{-1}D_{2}}\ast\cdots \end{align*} $$
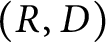 $(R,D)$
.
$(R,D)$
.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
This work was supported by the National Natural Science Foundation of China 11971194.
References
- 1
- Cited by



