Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T06:02:07.219Z Has data issue: false hasContentIssue false
  • English
  • Français

The Spherical Functions Related to the Root System B2

Published online by Cambridge University Press:  20 November 2018

P. Sawyer
P. Sawyer*
Affiliation:
Department of Mathematics and Computer Science Laurentian University Sudbury, Ontario P3E 2C6
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we give an integral formula for the eigenfunctions of the ring of differential operators related to the root system 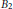${{B}_{2}}$.

Keywords

43A9022E3033C80
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 3 , 01 September 2002 , pp. 436 - 447
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Beerends, R. J., Some special values for the BC type hypergeometric function. Contemp.Math. 138 (1992), 138–1992.Google Scholar
[2] Heckman, G. J., Root systems and hypergeometric functions II. Compositio Math. 64 (1987), 64–1987.Google Scholar
[3] Heckman, G. J. and Opdam, E. M., Root systems and hypergeometric functions I. Compositio Math. 64 (1987), 64–1987.Google Scholar
[4] Helgason, Sigurdur, Group and Geometric Analysis. Academic Press, New York, 1984.Google Scholar
[5] Macdonald, I. G., Symmetric functions and Hall polynomials. 2nd Edition, Clarendon Press, Oxford, 1995.Google Scholar
[6] Ol'shanetskii, M. A. and Perelomov, A. M., Quantum systems that are connected to root systems, and radial parts. (Russian) Funktsional. Anal. i Prilozhen. (2) 12 (1978), 12–1978, 96.Google Scholar
[7] Opdam, E. M., Root systems and hypergeometric functions III. Compositio Math. 67 (1988), 67–1988.Google Scholar
[8] Opdam, E. M., Root systems and hypergeometric functions IV. Compositio Math. 67 (1988), 67–1988.Google Scholar
[9] Rudin, Walter, Real and Complex Analysis. McGraw Hill Series in Higher Mathematics, 2nd edition, 1974.Google Scholar
[10] Sawyer, P., Spherical functions on symmetric cones. Trans. Amer.Math. Soc. 349 (1997), 349–1997.Google Scholar
[11] Sawyer, P., The eigenfunctions of a Schrödinger operator associated to the root system An−1 . Quart. J. Math. Oxford Ser. 2 50 (1999), 50–1999.Google Scholar
[12] Sawyer, P., Spherical functions on SO0(p, q)= SO(p) × SO(q). Canad. Math. Bull. (4) 42 (1999), 42–1999.Google Scholar
[13] Sekiguchi, Jiro, An Euler type integral formula for zonal spherical functions on SO(m, 2)= SO(m) × SO(2). Bull. Univ. Electro-Comm. (1) 4 (1991), 4–1991.Google Scholar
[14] Smith, Kennan T., Primer of modern analysis. Bogden and Quigley, Inc., 1971.Google Scholar