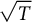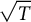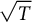Square roots of weighted shifts of multiplicity two

Abstract

Given a weighted shift T of multiplicity two, we study the set $\sqrt {T}$ of all square roots of T. We determine necessary and sufficient conditions on the weight sequence so that this set is non-empty. We show that when such conditions are satisfied, $\sqrt {T}$ contains a certain special class of operators. We also obtain a complete description of all operators in $\sqrt {T}$.

1 Introduction

Let $\mathcal {H}$ be a complex Hilbert space. We use $\mathcal {B}(\mathcal {H})$ to denote the algebra of all bounded linear operators on $\mathcal {H}$ . For $T\in \mathcal {B}(\mathcal {H})$ , we are interested in bounded operators Q for which $Q^2 = T$ . If such an operator exists, we say that T has a square root and in that case we would like to describe $\sqrt {T}$ , the set of all possible square roots of T. It is known that while many operators have an abundance of square roots, others do not have any square root at all. Lebow (see [6, Solution 111]) showed that when $\mathcal {H}$ is infinite-dimensional, the set of all square roots of zero is dense in $\mathcal {B}(\mathcal {H})$ in the strong operator topology. On the other hand, Halmos proved (see [5, p. 894]) that the unilateral shift S and more generally weighted shift operators do not have any square root. It was shown in [1] that the direct sum and the tensor product of S and its adjoint $S^{*}$ do not have square roots either. For properties of square and nth roots of normal and other classes of general operators, see the papers [3, 7–12, 14].

Our work was motivated by a recent paper [13] in which the authors provide complete descriptions of the set of all square roots of certain well-known classical operators. More specifically, square roots of the square of the unilateral shift, the Volterra operator, certain compressed shifts, the unilateral shift plus its adjoint, the Hilbert matrix, and the Cesàro operator are discussed. Particularly interesting to us is the square of the unilateral shift. Let us discuss this case in more details.

Recall that the Hardy space $H^2$ consists of all holomorphic functions $f(z) = \sum _{n=0}^{\infty }a_nz^n$ on the unit disk for which

$$\begin{align*}\|f\|_{H^2} = \Bigg(\sum_{n=0}^{\infty}|a_n|^2\Bigg)^{1/2} < \infty.\end{align*}$$

The set $\{e_n(z)=z^n: n=0,1,\ldots \}$ of monomials forms an orthonormal basis for $H^2$ . The unilateral shift on $H^2$ is defined as

$$\begin{align*}Se_{n} = e_{n+1}\ \text{ for all } n\geq 0. \end{align*}$$

We see that S is the same as the operator $M_{z}$ of multiplication by the variable z:

(1.1) $$ \begin{align} (Sf)(z) = (M_zf)(z) = zf(z),\quad f\in H^2. \end{align} $$

In [13, Section 2], a characterization of $\sqrt {S^2}$ is given. In addition to the trivial square root, which is S itself, [13, Remark 2.19(iii)] provides another simple but interesting square root, which acts on the orthonormal basis as follows: for $n\geq 0$ ,

(1.2) $$ \begin{align} \tilde{S}e_{n} = \begin{cases} e_{n+3}, & \text{ if } n \text{ is even},\\ e_{n-1}, & \text{ if } n \text{ is odd}. \end{cases} \end{align} $$

As it turns out later, weighted versions of S and $\tilde {S}$ play important roles in our study.

The unilateral shift is a special case of (unilateral) weighted shift operators. Let $\{e_n\}_{n=0}^{\infty }$ be a fixed orthonormal basis for $\mathcal {H}$ . A weighted shift is a linear operator A on $\mathcal {H}$ such that

$$\begin{align*}Ae_n = w_n e_{n+1},\end{align*}$$

for all $n\geq 0$ , where $w_n\in \mathbb {C}$ . Weighted shift operators were investigated in great details in [15]. It was shown (see [15, Corollary 3]) that if A is an injective weighted shift, then A has no bounded kth root for any $k\geq 2$ .

In this paper, we study square roots of $A^2$ for a general injective weighted shift A. More generally, we shall be interested in square roots of weighted shift operators of multiplicity two.

Definition 1.1 Let $\mathcal {H}$ be a Hilbert space with an orthonormal basis $\{e_n\}_{n=0}^{\infty }$ . A weighted shift of multiplicity two with weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ is a bounded linear operator T on $\mathcal {H}$ such that

$$\begin{align*}Te_n = \lambda_n e_{n+2},\end{align*}$$

for all $n\geq 0$ , where $\lambda _n\in \mathbb {C}$ .

We alert the reader that there is a more general notion of weighted shift operators of multiplicity two, but we restrict our attention to only those defined above. Since we assume that T is bounded, the weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ is bounded. We shall only consider the case T is injective, that is, $\lambda _n\neq 0$ for all $n\geq 0$ . Following the proof of [15, Corollary 1], it can be shown that any such T is unitarily equivalent to a weighted shift operator of multiplicity two with weight sequence $\{|\lambda _n|\}_{n=0}^{\infty }$ . Our goal is to find necessary and sufficient conditions on the weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ for which T has a square root and to determine all possible such square roots. Examples illustrating various scenarios will be presented.

2 Weighted Hardy spaces and multipliers

One of the crucial ingredients used in [13, Section 2] is the fact that $S^2$ , the square of the unilateral shift, is unitarily equivalent to the direct sum $S\oplus S$ . It turns out that any weighted shift operator of multiplicity two is also unitarily equivalent to the direct sum of two weighted shifts. In order to establish this result, we need the notion of weighted Hardy spaces (see, for example, [2, Chapter 2] and [15, Section 4]).

Let $\beta =\{\beta _n\}_{n=0}^{\infty }$ be a sequence of positive real numbers. The weighted Hardy space $H^2_{\beta }$ consists of all formal power series $f = \sum _{n=0}^{\infty }\hat {f}(n)z^n$ for which

$$\begin{align*}\|f\|_{H^2_{\beta}} = \Bigg(\sum_{n=0}^{\infty}|\hat{f}(n)|^2\beta_n^2\Bigg)^{1/2} < \infty.\end{align*}$$

The inner product of any two elements $f, g$ in $H^2_{\beta }$ is given by

$$\begin{align*}\langle f,g\rangle_{H^2_{\beta}} = \sum_{n=0}^{\infty}\hat{f}(n)\overline{\hat{g}(n)}\beta_n^2.\end{align*}$$

It is clear that $H^2_{\beta }$ has $\{\beta _n^{-1}z^n:\ n\geq 0\}$ as an orthonormal basis and hence the set of all polynomials, $\mathbb {C}[z]$ , is dense in $H^2_{\beta }$ .

If $\beta _n = 1$ for all n, then we obtain the Hardy space $H^2$ . In the case $\beta _n = \frac {1}{\sqrt {n+1}}$ for all n, we have the standard Bergman space $A^2$ . If $\beta _n = \sqrt {n+1}$ , then $H^2_{\beta }$ coincides with the Dirichlet space $\mathcal {D}$ .

We shall use $M_z$ to denote the operator of multiplication on $H^2_{\beta }$ by the function $\varphi (z) = z$ . It is immediate that $M_z$ is a weighted shift with weight sequence $\{\beta _{n+1}/\beta _n\}_{n=0}^{\infty }$ , so $M_z$ is bounded on $H^2_{\beta }$ if and only if

$$\begin{align*}\sup\left\{\frac{\beta_{n+1}}{\beta_n}: n=0,1,\ldots\right\} < \infty.\end{align*}$$

Let T be a weighted shift operator of multiplicity two with weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ such that $\lambda _n>0$ for all $n\geq 0$ . Define $\beta _0 = \omega _0 = 1$ and

(2.1) $$ \begin{align} \beta_k = \lambda_0\lambda_2\cdots\lambda_{2k-2},\quad \omega_{k} = \lambda_1\lambda_3\cdots\lambda_{2k-1}, \end{align} $$

for all $k\geq 1$ . We recall the direct sum

$$\begin{align*}H^2_{\beta}\oplus H^2_{\omega} = \Big\{(f,g): \ f\in H^2_{\beta},\ g\in H^2_{\omega}\Big\},\end{align*}$$

on which the inner product is given as

$$\begin{align*}\Big\langle (f_1,g_1),(f_2,g_2)\Big\rangle_{H^2_{\beta}\oplus H^2_{\omega}} = \langle f_1,f_2\rangle_{H^2_{\beta}} + \langle g_1,g_2\rangle_{H^2_{\omega}}.\end{align*}$$

Define $W:\mathcal {H}\rightarrow H^2_{\beta }\oplus H^2_{\omega }$ by

(2.2) $$ \begin{align} W\bigg(\sum_{n=0}^{\infty}\mu_ne_n\bigg) = \Bigg(\sum_{n=0}^{\infty}\frac{\mu_{2n}}{\beta_n}z^n, \sum_{n=0}^{\infty}\frac{\mu_{2n+1}}{\omega_n}z^n\Bigg). \end{align} $$

Note that

$$ \begin{align*} \Big\|W\bigg(\sum_{n=0}^{\infty}\mu_ne_n\bigg)\Big\|^2_{H^2_{\beta}\oplus H^2_{\omega}} & = \Big\|\sum_{n=0}^{\infty}\frac{\mu_{2n}}{\beta_n}z^n\Big\|_{H^2_{\beta}}^{2} + \Big\|\sum_{n=0}^{\infty}\frac{\mu_{2n+1}}{\omega_n}z^n\Big\|_{H^2_{\omega}}^2\\ & = \Bigg(\sum_{n=0}^{\infty}|\mu_{2n}|^2\Bigg) + \Bigg(\sum_{n=0}^{\infty}|\mu_{2n+1}|^2\Bigg)\\ & = \Big\|\sum_{n=0}^{\infty}\mu_ne_n\Big\|^2_{\mathcal{H}}. \end{align*} $$

So W is an isometry. On the other hand, the range of W is dense in $H^2_{\beta }\oplus H^2_{\omega }$ because it contains all pairs of monomials. As a result, W is a unitary operator. The inverse $W^{-1}:H^2_{\beta } \oplus H^2_{\omega } \rightarrow \mathcal {H}$ admits the formula

(2.3) $$ \begin{align} W^{-1}(f,g) = \sum_{n=0}^{\infty}\Big(\hat{f}(n)\beta_n\,e_{2n} + \hat{g}(n)\omega_n\,e_{2n+1}\Big), \end{align} $$

whenever $f=\sum _{n=0}^{\infty }\hat {f}(n)z^n \in H^2_{\beta }$ and $g=\sum _{n=0}^{\infty }\hat {g}(n)z^n \in H^2_{\omega }$ .

Proposition 2.1 Let T be a weighted shift of multiplicity two on $\mathcal {H}$ with weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ such that $\lambda _n>0$ for all $n\geq 0$ . Then T is unitarily equivalent to $M_z\oplus M_z$ on $H^2_{\beta }\oplus H^2_{\omega }$ for $\beta $ and $\omega $ defined as in (2.1). In fact, we have the following commutative diagram:

where W is given by (2.2).

Proof We first note that since T is assumed to be bounded, the weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ is bounded and hence $M_z$ is bounded on both $H^2_{\beta }$ and $H^2_{\omega }$ . For any $h = \sum _{n=0}^{\infty }\mu _ne_n\in \mathcal {H}$ , we have $T(h) = \sum _{n=0}^{\infty }\lambda_n \mu _ne_{n+2}$ and

$$\begin{align*} W^{-1} (M_z \oplus M_z) W(h) & = W^{-1} (M_z \oplus M_z)\left( \sum_{m=0}^{\infty} \frac{\mu_{2m}}{\beta_m}z^m,\sum_{n=0}^{\infty} \frac{\mu_{2n+1}}{\omega_n}z^n \right)\\ & = W^{-1} \left( \sum_{m=0}^{\infty} \frac{\mu_{2m}}{\beta_m}z^{m+1},\sum_{n=0}^{\infty} \frac{\mu_{2n+1}}{\omega_n}z^{n+1} \right)\\ & = \sum_{n=0}^{\infty}\Bigg(\frac{\mu_{2n}\beta_{n+1}}{\beta_n}\,e_{2n+2} + \frac{\mu_{2n+1}\omega_{n+1}}{\omega_n}\,e_{2n+3}\Bigg)\\ & = \sum_{n=0}^{\infty}\lambda_n\mu_ne_{n+2} \end{align*}$$

since $\beta _{n+1}/\beta _n = \lambda _{2n}$ and $\omega _{n+1}/\omega _{n} = \lambda _{2n+1}$ for all $n\geq 0$ . Therefore, we have $W^{-1}(M_{z}\oplus M_z)W = T$ as desired.

Proposition 2.1 shows that in order to study the square roots of T, we need to investigate the square roots of $M_z\oplus M_z$ . Let $A\in \mathcal {B}(H^2_{\beta }\oplus H^2_{\omega })$ be a square root of $M_z\oplus M_z$ . Then A must commute with $M_z\oplus M_z$ . Write

$$\begin{align*}A = \begin{bmatrix} A_{11} & A_{12}\\ A_{21} & A_{22} \end{bmatrix},\end{align*}$$

where $A_{11}: H^2_{\beta } \rightarrow H^2_{\beta }$ , $A_{12}: H^2_{\omega } \rightarrow H^2_{\beta }$ , $A_{21}: H^2_{\beta } \rightarrow H^2_{\omega }$ and $A_{22}: H^2_{\omega } \rightarrow H^2_{\omega }$ . Accordingly, we also write

$$\begin{align*}M_z\oplus M_z = \begin{bmatrix} M_z & 0\\ 0 & M_z \end{bmatrix}. \end{align*}$$

Because A is bounded on $H^2_{\beta }\oplus H^2_{\omega }$ , all operators $A_{ij}$ are bounded. Since A commutes with $M_z\oplus M_z$ , we have

(2.4) $$ \begin{align} A_{ij}M_z=M_zA_{ij}, \end{align} $$

for $i,j \in \{1,2\}$ . In order to obtain a characterization of such $A_{ij}$ , we need the notion of multipliers between two weighted Hardy spaces.

Let $\beta $ and $\omega $ be two sequences of positive real numbers. The multiplier space $\operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ is the set of all formal power series $\varphi $ such that $f\cdot \varphi $ belongs to $H^2_{\omega }$ for all $f\in H^2_{\beta }$ . We shall use $M_{\varphi }$ to denote the multiplication operator $f\mapsto f\cdot \varphi $ . We write $\operatorname {Mult}(H^2_{\beta })$ to denote the space of all multipliers of $H^2_{\beta }$ , that is, $\operatorname {Mult}(H^2_{\beta },H^2_{\beta })$ .

We list here two important facts about multipliers. The case $\beta = \omega $ was proved in [15, Section 4]. The proofs for $\beta \neq \omega $ are similar.

1. (M1) For any $\varphi \in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ , the operator $M_{\varphi }$ is bounded from $H^2_{\beta }$ into $H^2_{\omega }$ . We call the operator norm of $M_{\varphi }$ the multiplier norm of $\varphi $ .

2. (M2) If $\varphi \in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ and $\psi \in \operatorname {Mult}(H^2_{\omega },H^2_{\gamma })$ , then the product $\varphi \psi $ belongs to $\operatorname {Mult}(H^2_{\beta },H^2_{\gamma })$ and $M_{\psi }M_{\varphi } = M_{\psi \varphi }$ .

The following result generalizes the well-known fact that the commutant of the unilateral shift on the Hardy space $H^2$ is the set of all analytic Toeplitz operators.

Proposition 2.2 Let $\beta $ and $\omega $ be two sequences of positive real numbers. Suppose $R:H^2_{\beta }\longrightarrow H^2_{\omega }$ is a bounded linear operator such that

$$\begin{align*}M_{z}R = RM_{z},\end{align*}$$

where the left-side $M_z$ acts on $H^2_{\omega }$ , whereas the right-side $M_z$ acts on $H^2_{\beta }$ . Then there exists $\varphi \in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ such that $R = M_{\varphi }$ .

Remark 2.3 In the case $\beta = \omega $ , this result is well known (see [15, Theorem 3]). The proof for the general setting is quite similar, but for completeness, we provide here the details.

Proof For all integers $n\geq 0$ , we have $M_zR(z^n) = RM_z(z^n)$ , which gives

$$\begin{align*}z\cdot R(z^n) = R(z^{n+1}).\end{align*}$$

Define $\varphi = R(1)$ . It then follows that

$$\begin{align*}R(z^k) = \varphi\cdot z^k,\quad\forall\ k\geq 0.\end{align*}$$

By linearity, for any polynomial p in z,

$$\begin{align*}R(p) = \varphi \cdot p = M_{\varphi}p.\end{align*}$$

From this identity and the boundedness of R, there exists $B> 0$ such that

$$\begin{align*}\|\varphi \cdot p\|_{H^2_{\omega}} = \|R(p)\|_{H^2_{\omega}} \leq B\|p\|_{H^2_{\beta}}.\end{align*}$$

Because polynomials form a dense subset in $H^2_{\beta }$ , we conclude that $\varphi $ belongs to $\operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ . Since the bounded operators R and $M_{\varphi }$ agree on a dense subspace of $H^2_{\beta }$ , they are equal on all of $H^2_{\beta }$ . That is, $R=M_{\varphi }$ .

It is well known that $\operatorname {Mult}(H^2)$ and $\operatorname {Mult}(A^2)$ are both equal to $H^{\infty }$ , the algebra of all bounded holomorphic functions on the unit disk. However, the situation in the general setting becomes quite complicated. It is known that $\operatorname {Mult}(A^2,H^2)=\{0\}$ while $H^{\infty }\subsetneq \operatorname {Mult}(H^2,A^2)$ . Characterizations of multipliers between Hardy and Bergman spaces over the unit disk and over more general domains have been considered by several authors. See [4, 16, 17] and the references therein. In the results below, we offer some fundamental properties of $\operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ which will be needed for our work.

Proposition 2.4 Let $\varphi = \sum _{n=0}^{\infty }\hat {\varphi }(n)z^n$ belong to $\operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ . Then, for each $n\geq 0$ , if $\hat {\varphi }(n)\neq 0$ , then $z^n$ belongs to $\operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ .

Proof Consider the multiplication operator $M_{\varphi }: H^2_{\beta } \rightarrow H^2_{\omega }$ defined by $f \mapsto f \cdot \varphi $ for $f\in H^2_{\beta }$ . By property (M1), $M_{\varphi }$ is bounded, so there exists $B> 0$ such that for $f \in H^2_{\beta }$ ,

$$\begin{align*}\| M_{\varphi}f\|_{H^2_{\omega}} \leq B\|f\|_{H^2_{\beta}}.\end{align*}$$

Setting $f(z) = z^m$ gives

$$ \begin{align*} \Bigg(\sum_{n=0}^{\infty}\|\hat{\varphi}(n)z^{n+m}\|^2_{H^2_{\omega}}\Bigg)^{1/2} = \|M_{\varphi}(z^m)\|_{H^2_{\omega}} \leq B\|z^m\|_{H^2_{\beta}}. \end{align*} $$

It follows that for all integers $n, m \geq 0$ , we have

$$\begin{align*}\|\hat{\varphi}(n)z^{n+m}\|_{H^2_{\omega}} \leq B\|z^m\|_{H^2_{\beta}},\end{align*}$$

which implies

$$\begin{align*}\|z^{n+m}\|_{H^2_{\omega}} \leq \dfrac{B}{|\hat{\varphi}(n)|} \|z^m\|_{H^2_{\beta}}, \quad\forall\ m\geq 0,\end{align*}$$

provided that $\hat {\varphi }(n)\neq 0$ .

Now, suppose $f(z) = \sum _{m=0}^{\infty }\hat {f}(m)z^m\in H^2_{\beta }$ . We then have

$$ \begin{align*} \Big\|z^nf(z)\Big\|_{H^2_{\omega}}^2 & = \Big\|\sum_{m=0}^{\infty}\hat{f}(m)z^{n+m}\Big\|_{H^2_{\omega}}^2\\ & = \sum_{m=0}^{\infty}|\hat{f}(m)|^2\cdot\|z^{n+m}\|_{H^2_{\omega}}^2\\ & \leq\frac{B^2}{|\hat{\varphi}(n)|^2}\sum_{m=0}^{\infty}|\hat{f}(m)|^2\cdot\|z^{m}\|^2_{H^2_{\beta}}\\ & = \frac{B^2}{|\hat{\varphi}(n)|^2}\|f\|_{H^2_{\beta}}^2. \end{align*} $$

It follows that

$$\begin{align*}\|z^nf(z)\|_{H^2_{\omega}} \leq \frac{B}{|\hat{\varphi}(n)|}\|f\|_{H^2_{\beta}}.\end{align*}$$

Therefore, $z^n \in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ .

We now determine conditions for which the multiplier space $\operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ contains a nonzero element or when it contains all polynomials. Motivated by Proposition 2.1, we only consider weighted Hardy spaces on which the multiplication operator $M_z$ is bounded. Note that we use $\mathbb {C}[z]$ to denote the space of all polynomials in z.

Theorem 2.5 Let $\beta $ and $\omega $ be two sequences of positive real numbers such that $M_z$ is bounded on both $H^2_{\beta }$ and $H^2_{\omega }$ . Then:

1. (a) $\operatorname {Mult}(H^2_{\beta },H^2_{\omega }) \neq \{0\}$ if and only if $\Big (\operatorname {Mult}(H^2_{\beta },H^2_{\omega })\cap \mathbb {C}[z]\Big )\neq \{0\}$ if and only if there exists $k\geq 0$ such that

   $$\begin{align*}\sup\Bigg\{\frac{\omega_{n+k}}{\beta_n}:\ n = 0,1,\ldots\Bigg\} < \infty.\end{align*}$$

2. (b) $\mathbb {C}[z]\subseteq \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ if and only if

   $$\begin{align*}\sup\Bigg\{\frac{\omega_n}{\beta_n}:\ n = 0,1,\ldots\Bigg\} < \infty.\end{align*}$$

Proof We first prove $(a)$ . Suppose there exists $\varphi \in \operatorname {Mult}(H^2_{\beta },H^2_{\omega }) \backslash \{0\}$ . Then $\hat {\varphi }(n)\neq 0$ for some index $n\geq 0$ . Proposition 2.4 tells us that $z^n \in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ . Therefore, $\operatorname {Mult}(H^2_{\beta },H^2_{\omega })\cap \mathbb {C}[z]\neq \{0\}$ .

Let $0\neq p\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })\cap \mathbb {C}[z]$ with $\deg {p}=k \geq 0$ . By Proposition 2.4, $z^k \in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ and by Property (M1) of multipliers, the operator $M_{z^k}$ is bounded from $H^2_{\beta }$ into $H^2_{\omega }$ . Thus, there exists $C> 0$ such that for all $n \geq 0$ ,

$$\begin{align*}\|M_{z^k}(z^n)\|_{H^2_{\omega}} \leq C\|z^n\|_{H^2_{\beta}}. \end{align*}$$

Equivalently, for all $n \geq 0$ , we have

$$\begin{align*}\omega_{n+k} \leq C\beta_{n}. \end{align*}$$

Consequently,

$$\begin{align*}\sup\Bigg\{\frac{\omega_{n+k}}{\beta_n}:\ n = 0,1,\ldots\Bigg\} \leq C < \infty.\end{align*}$$

Now, suppose that the previous inequality holds. Then, for $\varphi \in H^2_{\beta }$ ,

$$\begin{align*}\Big\|z^k \sum_{n=0}^{\infty}\hat{\varphi}(n)z^n\Big\|_{H^2_{\omega}}^{2} = \sum_{n=0}^{\infty}|\hat{\varphi}(n)|^2\omega_{n+k}^2 \leq C^2\sum_{n=0}^{\infty}|\hat{\varphi}(n)|^2\beta_n^2 = C^2\|\varphi\|^2_{H^2_{\beta}} < \infty. \end{align*}$$

Thus, $z^k \in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ , which proves $\operatorname {Mult}(H^2_{\beta },H^2_{\omega }) \neq \{0\}$ .

Now, we prove $(b)$ . Suppose $\mathbb {C}[z]\subseteq \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ . Then, in particular, $1 \in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ . By Property (M1), there exists $C> 0$ such that for all $n \geq 0$ ,

$$\begin{align*}\|z^n\|_{H^2_{\omega}} \leq C \|z^n \|_{H^2_{\beta}}.\end{align*}$$

That is,

$$\begin{align*}\sup\Bigg\{\frac{\omega_n}{\beta_n}:\ n = 0,1,\ldots\Bigg\} \leq C < \infty.\end{align*}$$

Conversely, if the above supremum is finite, then as we have proved in $(a)$ , the constant function $1$ is a multiplier from $H^2_{\beta }$ into $H^2_{\omega }$ . Recall that we assume $M_z$ is bounded on $H^2_{\beta }$ , which implies that $z^k$ belongs to $\operatorname {Mult}(H^2_{\beta })$ for any $k\geq 0$ . Using Property (M2) of multipliers, we conclude that $z^k = 1\cdot z^k$ is an element of $\operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ . By linearity, it follows that $\mathbb {C}[z]\subseteq \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ .

Example 2.6 For each $n\geq 0$ , define $\omega _n = \frac {1}{k!}$ , where $k^2\leq n < (k+1)^2$ and define $\beta _n = \omega _{n+1}$ . Note that since $k! < k^{k} < (\sqrt {n})^{\sqrt {n}}$ ,

$$\begin{align*}1\geq \omega_n \geq \frac{1}{(\sqrt{n})^{\sqrt{n}}}\text{ for all } n.\end{align*}$$

Therefore, $\lim _{n\to \infty }\sqrt [n]{\omega _n} = 1$ , which implies that all elements of $H^2_{\omega }$ are holomorphic on the open unit disk $\mathbb {D}$ . We also have $\lim _{n\to \infty }\sqrt [n]{\beta _n}=1$ , so all elements of $H^2_{\beta }$ are holomorphic on $\mathbb {D}$ .

Since $\{\omega _n\}_{n=0}^{\infty }$ and $\{\beta _n\}_{n=0}^{\infty }$ are decreasing sequences, $M_z$ are bounded on both $H^2_{\omega }$ and $H^2_{\beta }$ . On the other hand,

$$\begin{align*}\sup\Bigg\{\frac{\omega_n}{\beta_n}:\ n=0,1,\ldots\Bigg\} = \sup\Bigg\{\frac{\omega_n}{\omega_{n+1}}:\ n=0,1,\ldots\Bigg\} = \infty,\end{align*}$$

so $1$ is not a multiplier from $H^2_{\beta }$ into $H^2_{\omega }$ . However,

$$\begin{align*}\sup\Bigg\{\frac{\beta_n}{\omega_n}:\ n=0,1,\ldots\Bigg\} = \sup\Bigg\{\frac{\omega_{n+1}}{\omega_{n}}:\ n=0,1,\ldots\Bigg\} < \infty,\end{align*}$$

so $1$ is a multiplier from $H^2_{\omega }$ into $H^2_{\beta }$ . In addition, since $\omega _{n+1}=\beta _n$ for all $n\geq 0$ , the operator $M_z$ is an isometry from $H^2_{\beta }$ into $H^2_{\omega }$ . Furthermore, Proposition 2.4 implies that for any $\varphi = \sum _{n=0}^{\infty }\hat {\varphi }(n)z^n\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ , we have $\hat {\varphi }(0)=0$ .

As we shall see in Section 3, the characterization of $\sqrt {M_z\oplus M_z}$ involves multipliers $a, b$ , and c satisfying the equation $a^2 + bc = z$ . We conclude this section with two results concerning such multipliers.

Lemma 2.7 Let $a = \sum _{n=0}^{\infty }\hat {a}(n)z^n, b = \sum _{n=0}^{\infty }\hat {b}(n)z^n$ , and $c = \sum _{n=0}^{\infty }\hat {c}(n)z^n$ be formal power series in z such that

$$\begin{align*}a^2 + bc = z.\end{align*}$$

Then exactly one of the following statements is true.

1. (1) $\hat {b}(0)\hat {c}(0)\neq 0$ .

2. (2) $\hat {b}(0) = 0$ , $\hat {b}(1)\neq 0$ , and $\hat {c}(0)\neq 0$ .

3. (3) $\hat {c}(0) = 0$ , $\hat {c}(1)\neq 0$ , and $\hat {b}(0)\neq 0$ .

In particular, both b and c are nonzero power series.

Proof By considering the constant coefficients and the coefficients of z on both sides of the equation $a^2 + bc = z$ , we have

$$\begin{align*}(\hat{a}(0))^2 + \hat{b}(0)\hat{c}(0) = 0\quad\text{ and }\quad 2\hat{a}(0)\hat{a}(1) + \hat{b}(0)\hat{c}(1) + \hat{b}(1)\hat{c}(0) = 1.\end{align*}$$

If $\hat {b}(0) = 0$ , then $\hat {a}(0) = 0$ and so $\hat {b}(1)\hat {c}(0) = 1$ , which implies that both $\hat {b}(1)$ and $\hat {c}(0)$ are nonzero. On the other hand, if $\hat {c}(0)=0$ , then $\hat {a}(0) = 0$ and so $\hat {b}(0)\hat {c}(1) = 1$ , which implies that both $\hat {c}(1)$ and $\hat {b}(0)$ are nonzero.

Proposition 2.8 Suppose $M_z$ is bounded on both $H^2_{\beta }$ and $H^2_{\omega }$ and there exist formal power series $a\in \operatorname {Mult}(H^2_{\beta })\cap \operatorname {Mult}(H^2_{\omega })$ , $b\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })$ , and $c\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ such that

$$\begin{align*}a^2 + bc = z.\end{align*}$$

Then $z\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })\cap \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ , and either $1\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })$ or $1\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ .

Proof Write $a = \sum _{n=0}^{\infty }\hat {a}(n)z^n, b = \sum _{n=0}^{\infty }\hat {b}(n)z^n$ , and $c = \sum _{n=0}^{\infty }\hat {c}(n)z^n$ . By Lemma 2.7, we have three cases to consider. First, suppose that $\hat {b}(0)\hat {c}(0)\neq 0$ . Then, by Proposition 2.4, the constant function $1$ is a multiplier from $H^2_{\beta }$ into $H^2_{\omega }$ and also from $H^2_{\omega }$ into $H^2_{\beta }$ . It follows that $H^2_{\beta } = H^2_{\omega }$ (with equivalent norms) and $\mathbb {C}[z]\subseteq \operatorname {Mult}(H^2_{\omega },H^2_{\beta })\cap \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ .

Second, consider the case $\hat {b}(0) = 0$ , $\hat {b}(1)\neq 0$ , and $\hat {c}(0)\neq 0$ . Then, by Proposition 2.4, $z\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })$ and $1\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ . Using Property (M2) of multipliers and the fact that $M_z$ is bounded on $H^2_{\omega }$ , we conclude that $z\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ as well.

Lastly, if $\hat {c}(0) = 0$ , $\hat {c}(1)\neq 0$ , and $\hat {b}(0)\neq 0$ , then a similar argument as in the second case proves that $1\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })$ and z belongs to $\operatorname {Mult}(H^2_{\omega },H^2_{\beta })\cap \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ .

3 Characterization of square roots

Proposition 2.1 shows that in order to study the square roots of weighted shifts of multiplicity two, we need to investigate the square roots of $M_z\oplus M_z$ . The following result offers the description of any such bounded square root. In the Hardy space case, we recover [13, Theorem 2.7], even though our statement is slightly different.

Theorem 3.1 Let $\beta $ and $\omega $ be two sequences of positive real numbers such that $M_z$ is bounded on both $H^2_{\beta }$ and $H^2_{\omega }$ . For $A\in \mathcal {B}(H^2_{\beta }\oplus H^2_{\omega })$ , the following statements are equivalent.

1. (a) $A^2 = M_z\oplus M_z$ .

2. (b) There exist $a\in \operatorname {Mult}(H^2_{\beta })\cap \operatorname {Mult}(H^2_{\omega })$ , $b\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })$ , and $c\in \operatorname {Mult}(H^2_{\beta }, H^2_{\omega })$ satisfying

   $$\begin{align*}a^2 + bc = z\end{align*}$$

   such that

   $$\begin{align*}A = \begin{bmatrix} M_{a} & M_{b}\\ M_{c} & -M_{a} \end{bmatrix}.\end{align*}$$

Proof Suppose $(a)$ holds. Write

$$\begin{align*}A = \begin{bmatrix} A_{11} & A_{12}\\ A_{21} & A_{22} \end{bmatrix},\end{align*}$$

where $A_{11}: H^2_{\beta } \rightarrow H^2_{\beta }$ , $A_{12}: H^2_{\omega } \rightarrow H^2_{\beta }$ , $A_{21}: H^2_{\beta } \rightarrow H^2_{\omega }$ , and $A_{22}: H^2_{\omega } \rightarrow H^2_{\omega }$ . As we have seen in (2.4), these are all bounded operators that satisfy

$$\begin{align*}A_{ij}M_z=M_zA_{ij},\end{align*}$$

for $i,j \in \{1,2\}$ . By Proposition 2.2, there exist power series $a\in \operatorname {Mult}(H^2_{\beta })$ , $b\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })$ , $c\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ , and $d \in \operatorname {Mult}(H^2_{\omega })$ such that

$$\begin{align*}A = \begin{bmatrix} M_{a} & M_{b}\\ M_{c} & M_{d} \end{bmatrix}.\end{align*}$$

Squaring A, we obtain

$$\begin{align*}\begin{bmatrix} M_{z} & 0\\ 0 & M_{z} \end{bmatrix} = A^2 = \begin{bmatrix} M_{a^2+bc} & M_{ab+bd}\\ M_{ca+dc} & M_{cb+d^2} \end{bmatrix},\end{align*}$$

which gives

$$\begin{align*}a^2 + bc = cb + d^2 = z\ \text{ and }\ b(a+d)= c(a + d) =0.\end{align*}$$

By Lemma 2.7, the first two identities imply that both b and c are nonzero power series. This, together with the last two identities and the fact that the ring of power series does not have zero divisors, gives $a+d = 0$ . Therefore, $d = -a$ and hence

$$\begin{align*}A = \begin{bmatrix} M_{a} & M_{b}\\ M_{c} & -M_{a} \end{bmatrix}\end{align*}$$

for $a\in \operatorname {Mult}(H^2_{\beta })\cap \operatorname {Mult}(H^2_{\omega })$ , $b\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })$ , and $c\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ satisfying $a^2 + bc = z$ .

Suppose now that $(b)$ holds. Then A is a bounded operator on $H^2_{\beta }\oplus H^2_{\omega }$ , and since $M_a$ commute with both $M_b$ and $M_c$ , we have

$$\begin{align*}A^2 = \begin{bmatrix} M_{a}M_{a} + M_{b}M_{c} & M_{a}M_{b}-M_{b}M_{a}\\ M_{c}M_{a}-M_{a}M_{c} & M_{c}M_{b}+M_{a}M_{a} \end{bmatrix} = \begin{bmatrix} M_{a^2 + bc} & 0\\ 0 & M_{a^2+bc} \end{bmatrix}. \end{align*}$$

Because $a^2 + bc = z$ , it follows that $A^2 = M_z\oplus M_z$ .

Theorem 3.1 combined with Proposition 2.8 provides us necessary and sufficient conditions for the existence of a bounded square root of $M_z\oplus M_z$ .

Proposition 3.2 Let $\beta $ and $\omega $ be two sequences of positive real numbers such that $M_z$ is bounded on both $H^2_{\beta }$ and $H^2_{\omega }$ . Consider $M_z\oplus M_z$ as a bounded operator on $H^2_{\beta }\oplus H^2_{\omega }$ . Then $\sqrt {M_z\oplus M_z}\neq \emptyset $ if and only if one (possibly both) of the following two cases occurs:

1. (a) $\sup \Big \{\frac {\omega _n}{\beta _n}:\ n = 0,1,\ldots \Big \}<\infty $ and $\sup \Big \{\frac {\beta _{n+1}}{\omega _n}:\ n = 0,1,\ldots \Big \}<\infty $ . In this case, $Q_{\mu } = \begin {bmatrix} 0 & \mu M_{z}\\ \mu ^{-1} & 0 \end {bmatrix}$ belongs to $\sqrt {M_z\oplus M_z}$ for all $\mu \neq 0$ .

2. (b) $\sup \Big \{\frac {\beta _n}{\omega _n}:\ n = 0,1,\ldots \Big \}<\infty $ and $\sup \Big \{\frac {\omega _{n+1}}{\beta _n}:\ n = 0,1,\ldots \Big \}<\infty $ . In this case, $R_{\mu } = \begin {bmatrix} 0 & \mu ^{-1}\\ \mu M_{z} & 0 \end {bmatrix}$ belongs to $\sqrt {M_z\oplus M_z}$ for all $\mu \neq 0$ .

Proof It is clear that if (a) or (b) holds, then $\sqrt {M_z\oplus M_z}$ is nonempty since it contains all $Q_{\mu }$ or $R_{\mu }$ (or both) for $\mu \neq 0$ .

Now, suppose that there exists a bounded operator A on $H^2_{\beta }\oplus H^2_{\omega }$ such that $A^2 = M_z\oplus M_z$ . Then, by Theorem 3.1,

$$\begin{align*}A = \begin{bmatrix} M_{a} & M_{b}\\ M_{c} & -M_{a} \end{bmatrix},\end{align*}$$

where $a\in \operatorname {Mult}(H^2_{\beta })\cap \operatorname {Mult}(H^2_{\omega })$ , $b\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })$ , and $c\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ satisfying $a^2 + bc = z$ . Using Proposition 2.8, we conclude that the multiplication operator $M_z$ is bounded from $H^2_{\beta }$ into $H^2_{\omega }$ and also from $H^2_{\omega }$ into $H^2_{\beta }$ . This implies that

$$\begin{align*}\sup\Bigg\{\frac{\omega_{n+1}}{\beta_n}:\ n = 0,1,\ldots\Bigg\}<\infty\ \text{ and }\ \sup\Bigg\{\frac{\beta_{n+1}}{\omega_n}:\ n = 0,1,\ldots\Bigg\}<\infty.\end{align*}$$

Furthermore, from Proposition 2.8, we have two cases. If $1\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ , then

$$\begin{align*}\sup\Bigg\{\frac{\omega_n}{\beta_n}:\ n = 0,1,\ldots\Bigg\}<\infty\end{align*}$$

and the matrix $Q_{\mu }$ represents a bounded operator on $H^2_{\beta }\oplus H^2_{\omega }$ for any $\mu \neq 0$ . A direct calculation shows $(Q_{\mu })^2 = M_z\oplus M_z$ . Therefore, (a) holds.

If $1\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })$ , then

$$\begin{align*}\sup\Bigg\{\frac{\beta_n}{\omega_n}:\ n = 0,1,\ldots\Bigg\}<\infty\end{align*}$$

and $R_{\mu }$ is a bounded operator on $H^2_{\beta }\oplus H^2_{\omega }$ , which satisfies $(R_{\mu })^2 = M_z\oplus M_z$ for all $\mu \neq 0$ . Hence, (b) holds.

Now, suppose that T is a weighted shift of multiplicity two with weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ such that $\lambda _n>0$ for all n. Proposition 3.2 and Theorem 3.1 describe all possible square roots of T. On the other hand, Propositions 2.1 and 3.2 together provide us a necessary and sufficient condition on the sequence $\{\lambda _n\}_{n=0}^{\infty }$ for the existence of bounded square roots of T. Recall that $\beta _0 = \omega _0 = 1$ and for all $n\geq 1$ ,

$$\begin{align*}\beta_n = \lambda_0\lambda_2\cdots\lambda_{2n-2},\quad\omega_n = \lambda_1\lambda_3\cdots\lambda_{2n-1}.\end{align*}$$

Theorem 3.3 Let $\mathcal {H}$ be a Hilbert space with an orthonormal basis $\{e_n\}_{n=0}^{\infty }$ . Let T be an injective weighted shift of multiplicity two with weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ with respect to $\{e_n\}_{n=0}^{\infty }$ . For any $Q\in \mathcal {B}(\mathcal {H})$ , the following statements are equivalent.

1. (a) $Q^2 = T$ .

2. (b) There exist power series $a\in \operatorname {Mult}(H^2_{\beta })\cap \operatorname {Mult}(H^2_{\omega })$ , $b\in \operatorname {Mult}(H^2_{\omega },H^2_{\beta })$ , and $c\in \operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ satisfying

   $$\begin{align*}a^2 + bc = z\end{align*}$$

   such that

   $$\begin{align*}Q = W^{-1}\begin{bmatrix} M_{a} & M_{b}\\ M_{c} & -M_{a} \end{bmatrix}W,\end{align*}$$

   where W is given by (2.2). Equivalently, for all integers $n\geq 0$ ,

   $$ \begin{align*} Q(e_{2n}) & = \sum_{m=n}^{\infty}\Bigg(\hat{a}(m-n)\frac{\beta_m}{\beta_n}e_{2m} + \hat{c}(m-n)\frac{\omega_m}{\beta_n}e_{2m+1}\Bigg),\\ Q(e_{2n+1}) & = \sum_{m=n}^{\infty}\Bigg(\hat{b}(m-n)\frac{\beta_m}{\omega_n}e_{2m} - \hat{a}(m-n)\frac{\omega_m}{\omega_n}e_{2m+1}\Bigg). \end{align*} $$
   We recall here that for a power series $\varphi $ , we use $\hat {\varphi }(j)$ to denote the coefficient of $z^j$ .

Proof By Proposition 2.1, we have $T=W^{-1}(M_z\oplus M_z)W$ . As a consequence, $Q^2 = T$ if and only if $Q = W^{-1}AW$ , where $A^2 = M_z\oplus M_z$ on $H^2_{\beta }\oplus H^2_{\omega }$ . The equivalence of (a) and (b) now follows from Theorem 3.1. To obtain the formulas for $Q(e_{2n})$ and $Q(e_{2n+1})$ , we note that

$$\begin{align*}W(e_{2n}) = \Bigg(\frac{1}{\beta_n}z^n,0\Bigg)\ \text{ and }\ W(e_{2n+1}) = \Bigg(0,\frac{1}{\omega_n}z^n\Bigg).\end{align*}$$

As a consequence,

$$\begin{align*}\begin{bmatrix} M_{a} & M_{b}\\ M_{c} & -M_{a} \end{bmatrix}W(e_{2n}) = \Bigg(\sum_{m=n}^{\infty}\frac{\hat{a}(m-n)}{\beta_n}z^m,\ \sum_{m=n}^{\infty}\frac{\hat{c}(m-n)}{\beta_n}z^m\Bigg)\end{align*}$$

and

$$\begin{align*}\begin{bmatrix} M_{a} & M_{b}\\ M_{c} & -M_{a} \end{bmatrix}W(e_{2n+1}) = \Bigg(\sum_{m=n}^{\infty}\frac{\hat{b}(m-n)}{\omega_n}z^m,\ -\sum_{m=n}^{\infty}\frac{\hat{a}(m-n)}{\omega_n}z^m\Bigg).\end{align*}$$

The required formulas then follow from the definition of $W^{-1}$ as in (2.3).

Theorem 3.4 Let T be an injective bounded weighted shift operator of multiplicity two with weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ . Then $\sqrt {T}\neq \emptyset $ if and only if there exists a positive constant C such that one (or both) of the following conditions holds:

1. (a) $\displaystyle \frac {1}{C}\cdot |\lambda _{2n}|\leq \Big |\frac {\lambda _1\lambda _3\cdots \lambda _{2n-1}}{\lambda _0\lambda _2\cdots \lambda _{2n-2}}\Big | \leq C$ for all $n\geq 1$ . In this case, for any $\mu \neq 0$ , the unilateral weighted shift $Q_{\mu }$ defined as $Q_{\mu }(e_j) = w_je_{j+1}$ is a bounded square root of T, where

   $$\begin{align*}w_j = \begin{cases} \mu, & \text{ if } j=0,\\ \lambda_0\mu^{-1}, & \text{ if } j=1,\\[2pt] \frac{\lambda_1\lambda_3\cdots\lambda_{2n-1}}{\lambda_0\lambda_2\cdots\lambda_{2n-2}}\mu, & \text{ if } j = 2n \text{ with } n\geq 1,\\[3pt] \frac{\lambda_0\lambda_2\cdots\lambda_{2n-2}\lambda_{2n}}{\lambda_1\lambda_3\cdots\lambda_{2n-1}}\mu^{-1}, & \text{ if } j = 2n+1 \text{ with } n\geq 1. \end{cases} \end{align*}$$

2. (b) $\displaystyle \frac {1}{C}\cdot |\lambda _{2n+1}|\leq \Bigg |\frac {\lambda _0\lambda _2\cdots \lambda _{2n-2}}{\lambda _1\lambda _3\cdots \lambda _{2n-1}}\Bigg | \leq C$ for all $n\geq 1$ . In this case, for any $\mu \neq 0$ , the operator $R_{\mu }$ defined as

   $$\begin{align*}R_{\mu}(e_j) = \begin{cases} w_je_{j+3}, & \text{ if } j \text{ is even}\\ w_je_{j-1}, & \text{ if } j \text{ is odd} \end{cases}\end{align*}$$

   is a bounded square root of T, where

   $$\begin{align*}w_j = \begin{cases} \lambda_1\mu, & \text{ if } j = 0,\\ \mu^{-1}, & \text{ if } j = 1,\\ \frac{\lambda_1\lambda_3\cdots\lambda_{2n-1}\lambda_{2n+1}}{\lambda_0\lambda_2\cdots\lambda_{2n-2}}\mu, & \text{ if } j=2n \text{ with } n\geq 1,\\[3pt] \frac{\lambda_0\lambda_2\cdots\lambda_{2n-2}}{\lambda_1\lambda_3\cdots\lambda_{2n-1}}\mu^{-1}, & \text{ if } j=2n+1 \text{ with } n\geq 1. \end{cases}\end{align*}$$

Proof As noted in the Introduction, T is unitarily equivalent to a weighted shift of multiplicity two with weight sequence $\{|\lambda _n|\}_{n=0}^{\infty }$ . Therefore, without loss of generality, we may assume that $\lambda _n>0$ for all n. Then, as in the proof of Theorem 3.3, a bounded operator Q is a square root of T if and only if $Q = W^{-1}AW$ , where A is a square root of $M_z\oplus M_z$ on $H^2_{\beta }\oplus H^2_{\omega }$ .

Note that for $n\geq 1$ ,

$$ \begin{align*} \frac{\omega_n}{\beta_n} = \frac{\lambda_1\lambda_3\cdots\lambda_{2n-1}}{\lambda_0\lambda_2\cdots\lambda_{2n-2}}, & \quad\quad \frac{\beta_{n+1}}{\omega_{n}} = \frac{\lambda_0\lambda_2\cdots\lambda_{2n}}{\lambda_1\lambda_3\cdots\lambda_{2n-1}} \end{align*} $$

and

$$ \begin{align*} \frac{\beta_n}{\omega_n} = \frac{\lambda_0\lambda_2\cdots\lambda_{2n-2}}{\lambda_1\lambda_3\cdots\lambda_{2n-1}}, & \quad\quad \frac{\omega_{n+1}}{\beta_{n}} = \frac{\lambda_1\lambda_3\cdots\lambda_{2n+1}}{\lambda_0\lambda_2\cdots\lambda_{2n-2}}. \end{align*} $$

The conclusion of the theorem then follows from Proposition 3.2. The formulas for $Q_{\mu }$ and $R_{\mu }$ follow from those in Theorem 3.3(b).

Remark 3.5 If $T = S^2$ , the square of the unilateral shift, then both conditions (a) and (b) hold. The operator $Q_{1}$ coincides with S, whereas $R_{1}$ is the same as $\tilde {S}$ defined in (1.2). For general T, while $Q_{\mu }$ is a weighted shift (a weighed version of S), the operator $R_{\mu }$ is a weighted version of $\tilde {S}$ . It is surprising that if $\sqrt {T}\neq \emptyset $ , then either weighted shifts or weighted versions of $\tilde {S}$ must be square roots of T.

Since both conditions (a) and (b) in Theorem 3.4 are invariant under taking pth powers for any $p>0$ , we obtain the following corollary.

Corollary 3.6 Let T be an injective bounded weighted shift operator of multiplicity two with weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ . Suppose T has bounded square roots. Then, for any $p>0$ , the weighted shift operator of multiplicity two with weight sequence $\{\lambda _n^p\}_{n=0}^{\infty }$ also possesses bounded square roots. (Here, $\lambda _n^p$ can be taken to be any $p{\text {th}}$ power of $\lambda _n$ .)

Example 3.7 Consider T the square of an injective bounded unilateral weighted shift with weight sequence $\{\delta _n\}_{n=0}^{\infty }$ . Then T is an injective weighted shift of multiplicity two whose weight sequence is given by $\lambda _n = \delta _{n}\delta _{n+1}$ for all $n\geq 0$ . Due to the fact that the sequence $\{\delta _n\}_{n=0}^{\infty }$ is bounded, a direct calculation shows that condition (a) in Theorem 3.4 holds. It follows that $Q_{\mu }\in \sqrt {T}$ for all $\mu \neq 0$ . In particular, for $\mu = \delta _0$ , we recover the original unilateral weighted shift.

On the other hand, since

$$\begin{align*}\frac{\lambda_0\lambda_2\cdots\lambda_{2n-2}}{\lambda_1\lambda_3\cdots\lambda_{2n-1}} = \frac{\delta_0}{\delta_{2n}},\end{align*}$$

condition (b) in Theorem 3.4 holds if and only if $|\delta _{2n}|\geq |\delta _0|/C$ for all $n\geq 0$ , that is, $\{|\delta _{2n}|\}_{n=0}^{\infty }$ is bounded away from zero. If this condition is not satisfied, then for $\mu \neq 0$ , the operator $R_{\mu }$ is not bounded, and hence cannot belong to $\sqrt {T}$ .

Example 3.8 In this example, we examine the square roots of $T=M_z^2$ on $H^2_{\gamma }$ for a class of weight sequences $\gamma = \{\gamma _n\}_{n=0}^{\infty }$ . We assume that $M_z$ is bounded on $H^2_{\gamma }$ . It is immediate that T is a weighted shift of multiplicity two with weight sequence $\{\lambda _n\}_{n=0}^{\infty }$ given by

$$\begin{align*}\lambda_n = \frac{\gamma_{n+2}}{\gamma_{n}},\quad n\geq 0.\end{align*}$$

Recall that with this T, we associate the sequences $\beta $ and $\omega $ defined by $\beta _0 = \omega _0 = 1$ and for $n\geq 1$ ,

$$\begin{align*}\beta_n = \lambda_0\lambda_2\cdots\lambda_{2n-2} = \frac{\gamma_{2n}}{\gamma_0}\ \text{ and }\ \omega_n = \lambda_1\lambda_3\cdots\lambda_{2n-1} = \frac{\gamma_{2n+1}}{\gamma_1}. \end{align*}$$

We assume further that there is a constant $C>1$ such that

$$\begin{align*}\frac{\gamma_n}{C}\leq \gamma_{2n}\leq C\gamma_n,\ \text{ and }\ \frac{\gamma_n}{C}\leq \gamma_{2n+1} \leq C\gamma_n\quad\text{ for all } n\geq 0. \end{align*}$$

(Note that these two conditions are satisfied by all the classical spaces including the Hardy, weighted Bergman, and Dirichlet spaces.) It then follows that the spaces $H^2_{\beta }$ , $H^2_{\omega }$ , and $H^2_{\gamma }$ are the same as sets and their norms are equivalent. As a consequence, the multiplier spaces $\operatorname {Mult}(H^2_{\beta })$ , $\operatorname {Mult}(H^2_{\omega })$ , $\operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ , and $\operatorname {Mult}(H^2_{\beta },H^2_{\omega })$ are all equal. Let us denote this common multiplier space by $\mathcal {M}$ . Theorem 3.3 asserts that a bounded operator Q on $H^2_{\gamma }$ is a square root of $M_z^2$ if and only if there exist $a,b,c\in \mathcal {M}$ satisfying $a^2 + bc = z$ such that

$$ \begin{align*} Q\Big(\frac{z^{2n}}{\gamma_{2n}}\Big) & = \sum_{m=n}^{\infty}\Bigg(\hat{a}(m-n)\frac{\beta_m}{\beta_n}\frac{z^{2m}}{\gamma_{2m}} + \hat{c}(m-n)\frac{\omega_m}{\beta_n}\frac{z^{2m+1}}{\gamma_{2m+1}}\Bigg)\\ & = \sum_{m=n}^{\infty}\Bigg(\hat{a}(m-n)\frac{z^{2m}}{\gamma_{2n}} +\hat{c}(m-n)\frac{\gamma_0}{\gamma_1}\frac{z^{2m+1}}{\gamma_{2n}} \Bigg), \end{align*} $$

which gives

$$\begin{align*}Q(z^{2n}) = \Bigg(a(z^2)+\frac{\gamma_0}{\gamma_1}z\cdot c(z^2)\Bigg)z^{2n}.\end{align*}$$

Similarly,

$$ \begin{align*} Q\Bigg(\frac{z^{2n+1}}{\gamma_{2n+1}}\Bigg) & = \sum_{m=n}^{\infty}\Bigg(\hat{b}(m-n)\frac{\beta_m}{\omega_n}\frac{z^{2m}}{\gamma_{2m}} - \hat{a}(m-n)\frac{\omega_m}{\omega_n}\frac{z^{2m+1}}{\gamma_{2m+1}}\Bigg)\\ & = \sum_{m=n}^{\infty}\Bigg(\frac{\gamma_1}{\gamma_0}\hat{b}(m-n)\frac{z^{2m}}{\gamma_{2n+1}} -\hat{a}(m-n)\frac{z^{2m+1}}{\gamma_{2n+1}}\Bigg), \end{align*} $$

which gives

$$\begin{align*}Q\Big(z^{2n+1}\Big) = \Bigg(\frac{\gamma_1}{\gamma_0}b(z) - z\cdot a(z^2)\Bigg)z^{2n}.\end{align*}$$

It follows that

$$\begin{align*}(Qg)(z) = \Bigg(a(z^2)+\frac{\gamma_0}{\gamma_1}z\cdot c(z^2)\Bigg)g_e(z) + \Bigg(\frac{\gamma_1}{\gamma_0}b(z^2) - z\cdot a(z^2)\Bigg)\frac{g_o(z)}{z}.\end{align*}$$

Here, for $g(z)= \ \sum _{n=0}^{\infty }\hat {g}(n)z^n\in H^2_{\gamma }$ , we define the even component $g_e(z) = \sum _{n=0}^{\infty }\hat {g}(2n)z^{2n}$ and the odd component $g_o(z) = \sum _{n=0}^{\infty }\hat {g}(2n+1)z^{2n+1}$ . Replacing $b(z)$ by $\frac {\gamma _0}{\gamma _1}b(z)$ and $c(z)$ by $\frac {\gamma _1}{\gamma _0}c(z)$ , we may write

(3.1) $$ \begin{align} (Qg)(z) = \Big(a(z^2)+z\cdot c(z^2)\Big)g_e(z) + \Big(b(z^2) - z\cdot a(z^2)\Big)\frac{g_o(z)}{z}. \end{align} $$

In the case $H^2_{\gamma }$ is the Hardy space or any weighted Bergman space over the unit disk, the multiplier space $\mathcal {M}$ is equal to $H^{\infty }$ . Formula (3.1) (with $a,b,c\in H^{\infty }$ ) then provides a complete description of all square roots of $M_z^2$ on these spaces.

We also remark that (3.1) becomes formula (2.20) in [13] if we replace $a(z)$ by $z\cdot a(z)$ and $c(z)$ by $z\cdot c(z)$ .

We conclude the paper with an example of a bounded weighted shift of multiplicity two which does not have any square root.

Example 3.9 Define $\lambda _{n}=1$ for all odd positive integers n. For even $n\geq 0$ , define $\lambda _n = 2$ or $\frac {1}{2}$ in the following pattern: $2$ appears once, $\frac {1}{2}$ appears twice, then $2$ appears four times, then $\frac {1}{2}$ appears eight times, and so on. The first several terms of the full sequence $\{\lambda _n\}_{n=0}^{\infty }$ are

$$\begin{align*}2,1,\frac{1}{2},1,\frac{1}{2},1,2,1,2,1,2,1,2,1,\frac{1}{2},1,\frac{1}{2},1,\frac{1}{2},1, \frac{1}{2},1,\frac{1}{2},1,\frac{1}{2},1,\frac{1}{2},1,\frac{1}{2},1,2,\ldots.\end{align*}$$

We see that

$$\begin{align*}\sup\Bigg\{\frac{\lambda_1\lambda_3\cdots\lambda_{2n-1}}{\lambda_0\lambda_2\cdots\lambda_{2n-2}}:\ n\geq 1\Bigg\} = \sup\Bigg\{\frac{1}{\lambda_0\lambda_2\cdots\lambda_{2n-2}}:\ n\geq 1\Bigg\} = \infty\end{align*}$$

and

$$\begin{align*}\sup\Bigg\{\frac{\lambda_0\lambda_2\cdots\lambda_{2n-2}}{\lambda_1\lambda_3\cdots\lambda_{2n-1}}:\ n\geq 1\Bigg\} = \sup\Bigg\{\lambda_0\lambda_2\cdots\lambda_{2n-2}:\ n\geq 1\Bigg\} = \infty.\end{align*}$$

Let T be a weighted shift operator of multiplicity two with the above weight sequence. It then follows from Theorem 3.4 that $\sqrt {T} = \emptyset $ .