Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T09:38:19.079Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of Traveling Wavefronts for a Two-Component Lattice Dynamical System Arising in Competition Models

Published online by Cambridge University Press:  20 November 2018

Guo-Bao Zhang  and
Ge Tian
Guo-Bao Zhang*
Affiliation:
College of Mathematics and Statistics, Northwest Normal University, Lanzhou, Gansu 730070, People’s Republic of China, e-mail: zhanggb2011@nwnu.edu.cn
Ge Tian
Affiliation:
College of Mathematics and Statistics, Northwest Normal University, Lanzhou, Gansu 730070, People’s Republic of China, e-mail: 945166426@qq.com
*
G.-B. Zhang is the corresponding author. Author G.-B. Z.was supported by NSF of China (11401478).
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study a two-component Lotka–Volterra competition systemon a one-dimensional spatial lattice. By the comparison principle, together with the weighted energy, we prove that the traveling wavefronts with large speed are exponentially asymptotically stable, when the initial perturbation around the traveling wavefronts decays exponentially as 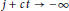$j\,+\,ct\,\to \,-\,\infty $, where 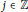$j\,\in \,\mathbb{Z}$, 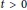$t\,>\,0$, but the initial perturbation can be arbitrarily large on other locations. This partially answers an open problem by J.-S. Guo and C.-H.Wu.

Keywords

34A3334K2092D25lattice dynamical systemcompetition modeltraveling wavefrontstability
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 2 , 01 June 2018 , pp. 423 - 437
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Cheng, C., Li, W.-T., and Wang, Z.-C., Spreading speeds and travelling waves in a delayed population model with stage structure on a 2D spatial lattice. IMA J. Appl. Math. 73 (2008), 592–618. http://dx.doi.org/10.1093/imamat/hxn003Google Scholar
[2] Cheng, C., Li, W.-T., and Wang, Z.-C., Asymptotic stability of traveling wavefronts in a delayed population model with stage structure on a two-dimensional spatial lattice. Discrete Contin. Dyn. Syst. Ser. B. 13 (2010), 559–575. http://dx.doi.Org/10.3934/dcdsb.2O10.13.559Google Scholar
[3] Guo, J.-S. and Liang, X., The minimal speed of traveling fronts for the Lotka-Volterra competition System. J. Dynam. Differential Equations 23 (2011), 353–363. http://dx.doi.Org/10.1007/s10884-011-9214-5Google Scholar
[4] Guo, J.-S. and Wu, C.-H., Wave propagation for a two-component lattice dynamical System arising in strong competition modeis. J. Differential Equations 250 (2011), 3504–3533. http://dx.doi.Org/10.1016/j.jde.2O10.12.004Google Scholar
[5] Guo, J.-S. and Wu, C.-H., Traveling wave front for a two-component lattice dynamical System arising in competition modeis. J. Differential Equations 252 (2012), 4357–4391. http://dx.doi.Org/10.1016/j.jde.2012.01.009Google Scholar
[6] Guo, J.-S. and Wu, C.-H., Recent developments on wave propagation in 2-species competition Systems. Discrete Contin. Dyn. Syst. Ser. B. 17 (2012), 2713–2724. http://dx.doi.org/10.3934/dcdsb.2012.17.2713Google Scholar
[7] Huang, R., Mei, M., and Wang, Y., Planar traveling waves for nonlocal dispersion equation with monostable nonlinearity. Discrete Contin. Dyn. Syst. 32 (2012), 3621–3649. http://dx.doi.org/10.3934/dcds.2012.32.3621Google Scholar
[8] Huang, R., Mei, M., Zhang, K.-J., and Zhang, Q.-F., Asymptotic stability of non-monotone traveling waves for time-delayed nonlocal dispersion equations. Discrete Contin. Dyn. Syst. 36 (2016), 1331–1353. http://dx.doi.org/10.3934/dcds.2016.36.1331Google Scholar
[9] Kan-on, Y. and Fang, Q., Stability of monotone traveling waves for competition-diffusion equations. Japan J. Indust. Appl. Math. 13 (1996), 343–349. http://dx.doi.org/10.1007/BF031 67252Google Scholar
[10] Li, W.-T., Zhang, L., and Zhang, G.-B., Invasion entire Solutions in a competition System with nonlocal dispersal. Discrete Contin. Dyn. Syst. 35 (2015), 1531–1560. http://dx.doi.org/10.3934/dcds.2015.35.1531Google Scholar
[11] Lin, C.-K., Lin, C.-T., Lin, Y.-P., and Mei, M., Exponential stability oj nonmonotone traveling waves for Nicholson's bbwflies equation. SIAM J. Math. Anal. 46 (2014), 1053–1084. http://dx.doi.Org/10.1137/120904391Google Scholar
[12] Lv, G. and Wang, M.-X., Nonlinear stability oj traveling wave fronts for nonlocal delayed reaction-diffusion equations. J. Math. Anal. Appl. 385 (2012), 1094–1106. http://dx.doi.Org/10.1016/j.jmaa.2O11.07.033Google Scholar
[13] Lv, G. and Wang, X.-H., Stability ojtraveling wave fronts for nonlocal delayed reaction diffusion Systems. J. Anal. Appl. 33 (2014), 463–480. http://dx.doi.Org/10.4171/ZAA/1 523Google Scholar
[14] Ma, S., and Duan, Y.-R., Asymptotic stability of traveling waves in a discrete convolution modelfor phase transitions. J. Math. Anal. Appl. 308 (2005), 240–256. http://dx.doi.Org/10.1016/j.jmaa.2005.01.011Google Scholar
[15] Ma, S. and Zhao, X.-Q., Global asymptotic stability of minimal fronts in monostable lattice equations. Discrete Contin. Dyn. Syst. 21 (2008), 259–275. http://dx.doi.org/10.3934/dcds.2008.21.259Google Scholar
[16] Ma, S., and Zou, X., Existence, uniqueness and stability of traveling waves in a discrete reaction-diffusion monostable equation with delay. J. Differential Equations 217 (2005), 54–87. http://dx.doi.Org/10.1016/j.jde.2005.05.004Google Scholar
[17] Martin, R.-H. and Smith, H.-L., Abstract functional-differential equations and reaction-diffusion Systems. Trans. Amer. Math. Soc. 321 (1990), 1–44. http://dx.doi.Org/10.2307/2001590Google Scholar
[18] Mei, M., So, J.-W.-H., Li, M.-Y., and Shen, S.-S.-P., Asymptotic stability of traveling waves for the Nicholson's blowflies equation with diffusion. Proc. Royal Soc. Edinburgh. 134A(2004), 579–594.Google Scholar
[19] Mei, M., and So, J.-W.-H., Stability ofstrong traveling waves for a nonlocal time-delayed reaction-diffusion equation. Proc. Royal Soc. Edinburgh. 138A(2008), 551–568. http://dx.doi.Org/10.1017/S0308210506000333Google Scholar
[20] Mei, M., Lin, C.-K., Lin, C.-T., and So, J.-W.-H., Traveling wavefronts for time-delayed reaction-diffusion equation. I. Local nonlinearity. J. Differential Equations 247 (2009), 495–510. http://dx.doi.Org/10.1016/j.jde.2008.12.026Google Scholar
[21] Mei, M., Lin, C.-K., Lin, C.-T., and So, J.-W.-H., Traveling wavefronts for time-delayed reaction-diffusion equation. II. Nonlocal nonlinearity. J. Differential Equations 247 (2009), 511–529. http://dx.doi.Org/10.1016/j.jde.2008.12.020Google Scholar
[22] Mei, M. and Wong, Y.-S., Novel stability resultsfor traveling wavefronts in an age-structured reaction-diffusion equation. Math. Biosci. Eng. 6(2009), 743–752. http://dx.doi.Org/10.3934/mbe.2009.6.743Google Scholar
[23] Mei, M., Ou, C., and Zhao, X.-Q., Global stability of monostable traveling waves for nonlocal time-delayed reaction-diffusion equations. SIAM J. Math. Anal. 42 (2010), 2762–2790. http://dx.doi.Org/10.1137/090776342Google Scholar
[24] Smith, H.-L. and Zhao, X.-Q., Global asymptotic stability of traveling waves in delayed recation-diffusion equations. SIAM J. Math. Anal. 31 (2000), 514–534. http://dx.doi.Org/10.1137/S0036141098346785Google Scholar
[25] Tian, G. and Zhang, G.-B., Stabilty of traveling wavefronts for a discrete diffusive Lotka-Volterra competition System. J. Math. Anal. Appl. 447 (2017), 222–242. http://dx.doi.Org/10.1016/j.jmaa.2O16.10.012Google Scholar
[26] Yang, Y., Li, W.-T., and Wu, S., Exponential stability of traveling fronts in a diffusion epidemic System with delay. Nonlinear Anal. Real World Appl. 12 (2011), 1223–1234. http://dx.doi.Org/10.1016/j.nonrwa.2010.09.017Google Scholar
[27] Yang, Y., Li, W.-T., and Wu, S., Stability of traveling waves in a monostable delayed System without quasi-monotonicity. Nonlinear Anal. Real World Appl. 3 (2013), 1511–1526. http://dx.doi.Org/10.1016/j.nonrwa.2012.10.015Google Scholar
[28] Yu, Z.-X., Xu, F., and Zhang, W-G., Stability of Invasion traveling waves for a competition System with nonlocal dispersals. Appl. Anal. 96 (2017), 1107–1125. http://dx.doi.Org/10.1080/00036811.2016.1178242Google Scholar
[29] Yu, Z.-X. and Yuan, R., Nonlinear stability of wavefronts for a delayed stage-structured population model on 2-D lattice. Osaka J. Math. 50(2013) 963–976.Google Scholar
[30] Yu, Z.-X. and Mei, M., Uniqueness and stability of traveling waves for cellular neural networks with multiple delays. J. Differential Equations 260, (2016), 241–267. http://dx.doi.org/10.1016/j.jde.2O15.08.037Google Scholar
[31] Zhang, G.-B., Global stability oftraveling wave fronts for non-local delayed lattice differential equations. Nonlinear Anal. Real World Appl. 13 (2012), 1790–1801. http://dx.doi.Org/10.1016/j.nonrwa.2011.12.010Google Scholar
[32] Zhang, G.-B. and Li, W.-T., Nonlinear stability oftraveling wavefronts in an age-structured population model with nonlocal dispersal and delay. Z. Angew. Math. Phys. 64 (2013), 1643–1659. http://dx.doi.Org/10.1007/s00033-013-0303-7Google Scholar
[33] Zhang, G.-B. and Ma, R., Spreading speeds and traveling wavesfor a nonlocal dispersal equation with convolution type crossing-monostable nonlinearity. Z. Angew. Math. Phys. 65 (2014), 819–844. http://dx.doi.Org/10.1007/s00033-013-0353-xGoogle Scholar