Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T17:35:04.525Z Has data issue: false hasContentIssue false
  • English
  • Français

Strong and Quasistrong Disconjugacy

Published online by Cambridge University Press:  20 November 2018

David London  and
Binyamin Schwarz
David London
Affiliation:
Department of Mathematics Technion, I.I.T., Haifa Israel
Binyamin Schwarz
Affiliation:
Department of Mathematics Technion, I.I.T., Haifa Israel
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A complex linear homogeneous differential equation of the nth order is called strong disconjugate in a domain G if, for every n points z1,…, zn in G and for every set of positive integers, k1…, kl, k1 + … + kl = n, the only solution y(z) of the equation which satisfies

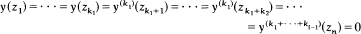
is the trivial one y(z) = 0. The equation y(n)(z) = 0 is strong disconjugate in the whole plane and for every other set of conditions of the form y(mk(zk) = 0, k = 1 , . . . , n, m1 ≤ m2... mn, there exist, in any given domain, points z1 , . . . , zn and nontrivial polynomials of degree smaller than n, which satisfy these conditions. An analogous results holds also for real disconjugate differential equations.

Keywords

34C10
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 25 , Issue 4 , 01 December 1982 , pp. 435 - 440
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. Coppel, W. A., "Disconjugacy", Lecture Notes in Mathematics 220, Springer Berlin, 1971.Google Scholar
2. Elias, U., The extremal solutions of the equation Ly + p(x)y = 0, II J. Math. Anal. Appl. 55 (1976), 253-265.Google Scholar
3. Lavie, M., On disconjugacy and interpolation in the complex domain J. Math. Anal. Appl. 32 (1970), 246-263.Google Scholar
4. London, D. and Schwarz, B., Disconjugacy of complex differential systems and equations, Trans. Am. Math. Soc. 135 (1969), 487-505.Google Scholar
5. Marden, M., "Geometry of Polynomials", 2nd ed., Amer. Math. Soc. Providence R.I., 1966.Google Scholar
6. Pólya, G., On the mean-value theorem corresponding to a given linear homogeneous differential equation, Trans. Am. Math. Soc. 24 (1922), 312-324.Google Scholar
7. Schwarz, B., Norm conditions for disconjugacy of complex differential systems, J. Math. Anal. Appl., 28 (1969), 553-568.Google Scholar
8. Wejntrob, L., Distribution of zeros of a solution for a nondisconjugate differential equation, J. Math. Anal. Appl. 55 (1976), 453-465.Google Scholar