Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T20:09:12.794Z Has data issue: false hasContentIssue false
  • English
  • Français

Subalgebras of gcN and Jacobi Polynomials

Published online by Cambridge University Press:  20 November 2018

Alberto De Sole  and
Victor G. Kac
Alberto De Sole
Affiliation:
Department of Mathematics MIT 77 Massachusetts Avenue Cambridge, MA 02139 USA, email: desole@math.mit.edu
Victor G. Kac
Affiliation:
Department of Mathematics MIT 77 Massachusetts Avenue Cambridge, MA 02139 USA, email: kac@math.mit.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

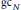We classify the subalgebras of the general Lie conformal algebra $\text{g}{{\text{c}}_{N}}$ that act irreducibly on 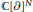$\mathbb{C}\,{{\left[ \partial \right]}^{N}}$ and that are normalized by the 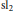$\text{s}{{\text{l}}_{2}}$-part of a Virasoro element. The problem turns out to be closely related to classical Jacobi polynomials 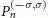$P_{n}^{\left( -\sigma ,\sigma \right)}$, 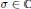$\sigma \,\in \,C$. The connection goes both ways—we use in our classification some classical properties of Jacobi polynomials, and we derive from the theory of conformal algebras some apparently new properties of Jacobi polynomials.

Keywords

17B6517B6817B6933C45
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 4 , 01 December 2002 , pp. 567 - 605
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Andrews, G. E., Askey, R. and Roy, R., Special Functions. Encyclopedia of Mathematics and its Applications 71, Cambridge University Press, 1999.Google Scholar
[2] Bakalov, B. N., Georgiev, L. S. and Todorov, I. T., A QFT approach to W1+∞ . In: Proceedings of the 2nd Bulgarian Workshop (eds. A. Ganchev et al.), Razlog, 1995.Google Scholar
[3] Boyallian, C., Kac, V. G. and Liberati, J., On the classification of subalgebras of CendN and gcN . Preprint, math-ph/0203022; J. Algebra, to appear.Google Scholar
[4] Cheng, S.-J., Kac, V. G. and Wakimoto, M., Extensions of Conformal Modules. In: Topological field theory, primitive forms and related topics (Kyoto, 1996), Progr.Math. 160, Birkhauser, Boston, 1996, 33–57.Google Scholar
[5] D'Andrea, A. and Kac, V. G., Structure theory of finite conformal algebras. Selecta Math. (3) 4 (1998), 377–418.Google Scholar
[6] Kac, V. G., Vertex algebras for beginners. 2nd edition, University Lecture Series 10, Amer.Math. Soc., Providence, RI, 1998.Google Scholar
[7] Rahman, M., A nonnegative representation of the linearization coefficients of the product of Jacobi polynomials. Canad. J. Math. (4) 33 (1981), 915–928.Google Scholar
[8] Yamamoto, G., Algebraic structures on quasi-primary states in superconformal algebras. Preprint.Google Scholar