Published online by Cambridge University Press: 20 November 2018
Let (αn.k) be a sequence of positive numbers. We define a regular sequence (resp. a weakly regular sequence) and then show the existence of a unitary operator (resp. a contraction T) L2[0, 1] → L2[0, 1] and a function f ∊ L2[0, 1] such that the pointwise convergence of the sequence of functions  is not satisfied almost surely. As a first corollary the pointwise convergence of the Abel means of a contraction from L2 into L2 does not hold necessarily almost surely. As a second corollary there exists a contraction T for which the means (and powers) of Brunei's operator A do not converge pointwise a.s. We also show that, for P > 1 fixed, there exists a sequence of positive numbers αn.k for which we have the pointwise convergence in LP of the sequence of polynomials
is not satisfied almost surely. As a first corollary the pointwise convergence of the Abel means of a contraction from L2 into L2 does not hold necessarily almost surely. As a second corollary there exists a contraction T for which the means (and powers) of Brunei's operator A do not converge pointwise a.s. We also show that, for P > 1 fixed, there exists a sequence of positive numbers αn.k for which we have the pointwise convergence in LP of the sequence of polynomials 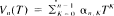 where T is a contraction of L1 and Lα. The dominated theorem does not, however, always hold for such LP-contractions.
where T is a contraction of L1 and Lα. The dominated theorem does not, however, always hold for such LP-contractions.