Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T05:25:35.411Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetric Products of Equivariantly Formal Spaces

Published online by Cambridge University Press:  20 November 2018

Matthias Franz
Matthias Franz*
Affiliation:
Department of Mathematics, University of Western Ontario, London, ON N6A 5B7 email: mfranz@uwo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 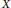$X$ be a 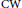$\text{CW}$ complex with a continuous action of a topological group 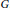$G$. We show that if 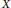$X$ is equivariantly formal for singular cohomology with coefficients in some field $\Bbbk $, then so are all symmetric products of 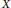$X$ and in fact all its $\Gamma $-products. In particular, symmetric products of quasi-projective 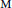$\text{M}$-varieties are again 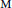$\text{M}$-varieties. This generalizes a result by Biswas and D’Mello about symmetric products of 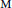$\text{M}$-curves. We also discuss several related questions.

Keywords

55N9155S1514P25symmetric productequivariant formalitymaximal varietyGamma product
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 2 , 01 June 2018 , pp. 272 - 281
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Allday, C., Cohomological aspects oftorus actions. In: Toric topology (Osaka, 2006), Contemp. Math., 460, American Mathematical Society, Providence, RI, 2008, pp. 29–36.http://dx.doi.Org/10.1090/conm/460/09008 Google Scholar
[2] Allday, C., Franz, M., and Puppe, V., Equivariant cohomology, syzygies and orbit structure. Trans. Amer. Math. Soc. 366(2014), no. 12, 6567–6589.http://dx.doi.org/10.1090/S0002-9947-2014-06165-5 Google Scholar
[3] Baird, T. J., Symmetrie produets ofa real curve and the moduli Space ofHiggs bundles. arxiv:1611.09636v3Google Scholar
[4] Biswas, I. and D'Mello, S., M-curves and Symmetrie produets. arxiv:1603.00234v1Google Scholar
[5] tom Dieck, T., Transformation groups. De Gruyter Studies in Mathematics, 8, Walter de Gruyter, Berlin 1987. http://dx.doi.org/10.1515/9783110858372 Google Scholar
[6] Dold, A., Homology of Symmetrie produets and other funetors of complexes. Ann. of Math. (2) 68(1958), 54–80.http://dx.doi.Org/10.2307/1970043 Google Scholar
[7] Dold, A., Lectures on algebraic topology. Second ed., Grundlehren der Mathematischen Wissenschaften, 200, Springer, Berlin-New York, 1980.Google Scholar
[8] Dolgachev, I., Lectures on invariant theory. London Mathematical Society Lecture Note Series, 296, Cambridge University Press, Cambridge, 2003.http://dx.doi.Org/10.1017/CBO9780511615436 Google Scholar
[9] Frankel, T., Fixedpoints and torsion on Kähler manifolds. Ann. of Math.(2) 70(1959), 1–8.http://dx.doi.Org/10.2307/1969889 Google Scholar
[10] Franz, M., Syzygies in equivariant cohomology for non-abelian Lie groups. In: Configuration Spaces (Cortona, 2014), Springer INdAM Ser., 14, Springer, Cham, 2016, pp. 325–360.http://dx.doi.org/10.1007/978-3-319-31580-5J4 Google Scholar
[11] Goresky, M., Kottwitz, R., and MacPherson, R., Equivariant cohomology, Koszul duality, and the localization theorem. Invent. Math. 131(1998), 25–83.http://dx.doi.org/10.1007/s002220050197 Google Scholar
[12] Gugenheim, V. K. A. M., On the chain-complex ofafibration. Illinois J. Math. 16(1972), 398–414.http://projecteuclid.org/euclid.ijm/1256065766 Google Scholar
[13] Illman, S., Smooth equivariant triangulations of G-manifolds for G afinite group. Math. Ann. 233(1978), 199–220.http://dx.doi.org/10.1007/BF01405351 Google Scholar
[14] Illman, S., Existence and uniqueness of equivariant triangulations of smooth proper G-manifolds with some applications to equivariant Whitehead torsion. J. Reine Angew. Math. 524(2000), 129–183.http://dx.doi.org/10.1515/crll.2000.054 Google Scholar
[15] Kirwan, F., Cohomology of quotients in symplectic and algebraic geometry. Mathematical Notes, 31, Princeton University Press, Princeton, NJ, 1984.http://dx.doi.Org/10.1007/BF01145470 Google Scholar
[16] Lamotke, K., Semisimpliziale algebraische Topologie. Grundlehren der mathematischen Wissenschaften, 147, Springer-Verlag, Berlin, 1968.http://dx.doi.org/10.1007/978-3-662-12988-3 Google Scholar
[17] May, J. P., Simplicial objects in algebraic topology. Chicago Lectures in Mathematics, Chicago of University Press, Chicago, IL, 1992.Google Scholar
[18] McCleary, J., A user's guide to spectral sequences. Second ed., Cambridge Studies in Advanced Mathematics, 58, Cambridge University Press, Cambridge, 2001.Google Scholar
[19] Smith, L., Homological algebra and the Eilenberg-Moore spectral sequence. Trans. Amer. Math. Soc. 129(1967), 58–93.http://dx.doi.org/10.1090/S0002-9947-1967-0216504-6 Google Scholar
[20] Totaro, B., Chow groups, Chow cohomology, and linear varieties. Forum Math. Sigma 2(2014), el7.http://dx.doi.Org/10.1017/fms.2014.15 Google Scholar
[21] Weber, A., Formality of equivariant intersection cohomology of algebraic varieties. Proc. Amer. Math. Soc. 131(2003), 2633–2638. http://dx.doi.org/10.1090/S0002-9939-03-07138-7 Google Scholar