Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T19:34:08.845Z Has data issue: false hasContentIssue false
  • English
  • Français

A Theorem on Unit-Regular Rings

Published online by Cambridge University Press:  20 November 2018

Tsiu-Kwen Lee  and
Yiqiang Zhou
Tsiu-Kwen Lee
Affiliation:
Department of Mathematics, National Taiwan University, Taipei 106, Taiwan e-mail: tklee@math.ntu.edu.tw
Yiqiang Zhou
Affiliation:
Department of Mathematics and Statistics, Memorial University of Newfoundland, St.John’s, NL A1C 5S7 e-mail: zhou@math.mun.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $R$ be a unit-regular ring and let $\sigma $ be an endomorphism of $R$ such that 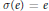$\sigma \left( e \right)\,=\,e$ for all 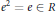${{e}^{2}}\,=\,e\,\in \,R$ and let 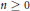$n\,\ge \,0$. It is proved that every element of 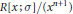$R[x;\,\sigma ]/\left( {{x}^{n+1}} \right)$ is equivalent to an element of the form 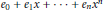${{e}_{0}}\,+\,{{e}_{1}}x\,+\,\cdots \,+\,{{e}_{n}}{{x}^{n}}$, where the ${{e}_{i}}$ are orthogonal idempotents of $R$. As an application, it is proved that 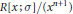$R[x;\,\sigma ]/\left( {{x}^{n+1}} \right)$ is left morphic for each 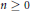$n\,\ge \,0$.

Keywords

16E5016U9916S7016S35morphic ringsunit-regular ringsskew polynomial rings
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 2 , 01 June 2010 , pp. 321 - 326
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Chen, J. and Zhou, Y., Morphic rings as trivial extensions. Glasgow Math. J. 47(2005), no. 1, 139–148. doi:10.1017/S0017089504002125Google Scholar
[2] Ehrlich, G., Units and one-sided units in regular rings. Trans. Amer. Math. Soc. 216(1976), 81–90. doi:10.2307/1997686Google Scholar
[3] Goodearl, K. R., von Neumann Regular Rings. Second edition. Robert E. Krieger Publishing, Malabar, FL, 1991.Google Scholar
[4] Lee, T.-K. and Zhou, Y., Morphic rings and unit-regular rings. J. Pure Appl. Algebra 210(2007), no. 2, 501–510. doi:10.1016/j.jpaa.2006.10.005Google Scholar
[5] Nicholson, W. K. and Campos, E. Sánchez, Rings with the dual of the isomorphism theorem. J. Algebra 271(2004), no. 1, 391–406. doi:10.1016/j.jalgebra.2002.10.001Google Scholar