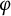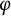1 Introduction
In recent decades, fractional differential equations are receiving great attention as a significant tool in pure and applied mathematics, finding applications in various fields such as propagation in complex mediums, epidemiology, biological tissues, computer vision (a survey), and the theory of viscoelasticity (see, for example, [Reference Atangana, Cattani, Srivastava and Yang9, Reference Soczkiewicz29]). Some basic results can be found in [Reference Abbas, Benchohra and N’Guérékata1, Reference Kilbas, Srivastava and Trujillo20, Reference Zhou, Wang and Zhang37].
The concept of the fractional derivative (FD) with regard to another function in the sense of Riemann–Liouville was presented by Kilbas et al. in [Reference Kilbas, Srivastava and Trujillo20]. The authors in [Reference Vanterler da C. Sousa and Capelas de Oliveira30] proposed a
![]() $\varphi $
-Hilfer FD and extended the work dealing with the Hilfer’s FD in [Reference Furati, Kassim and Tatar17]. The
$\varphi $
-Hilfer FD and extended the work dealing with the Hilfer’s FD in [Reference Furati, Kassim and Tatar17]. The
![]() $\varphi $
-Hilfer’s FD significance stems from the fact that it has as its special instances a number of widely used FD operators. As a matter of fact, the weakly singular kernel function in the fractional operator definition can be freely selected. In other words, it covers a wide range of cases for a specific function
$\varphi $
-Hilfer’s FD significance stems from the fact that it has as its special instances a number of widely used FD operators. As a matter of fact, the weakly singular kernel function in the fractional operator definition can be freely selected. In other words, it covers a wide range of cases for a specific function
![]() $\varphi $
. For some recent developments, see [Reference Arora, Mathur, Agarwal, Tiwari and Gupta7–Reference Asma, Rahman and Javed8, Reference Norouzi and N’Guérékata27, Reference Vanterler da C. Sousa and Capelas de Oliveira31, Reference Vanterler da C. Sousa and Capelas de Oliveira33–Reference Vanterler da C. Sousa, Rodrigues and Capelas de Oliveira35]. This kind of FD has been widely used in practical applications, such as, several anomalous diffusions, including ultra-slow processes [Reference Kosztołowicz and Dutkiewicz21], financial crisis [Reference Norouzi and N’Guérékata27], and random walks [Reference Fan, Wu and Fu16]. On the other side, the modeling of various natural phenomena in chemistry, biology, computer networks, and physics often involves different types of coupled fractional differential systems, as evidenced by references [Reference Samadi, Ntouyas and Tariboon28, Reference Zentar, Ziane and Khelifa36]. Therefore, investigating of coupled systems within the context of the
$\varphi $
. For some recent developments, see [Reference Arora, Mathur, Agarwal, Tiwari and Gupta7–Reference Asma, Rahman and Javed8, Reference Norouzi and N’Guérékata27, Reference Vanterler da C. Sousa and Capelas de Oliveira31, Reference Vanterler da C. Sousa and Capelas de Oliveira33–Reference Vanterler da C. Sousa, Rodrigues and Capelas de Oliveira35]. This kind of FD has been widely used in practical applications, such as, several anomalous diffusions, including ultra-slow processes [Reference Kosztołowicz and Dutkiewicz21], financial crisis [Reference Norouzi and N’Guérékata27], and random walks [Reference Fan, Wu and Fu16]. On the other side, the modeling of various natural phenomena in chemistry, biology, computer networks, and physics often involves different types of coupled fractional differential systems, as evidenced by references [Reference Samadi, Ntouyas and Tariboon28, Reference Zentar, Ziane and Khelifa36]. Therefore, investigating of coupled systems within the context of the
![]() $\varphi $
-Hilfer FD framework became recently crucial, for more background, see [Reference Abdo, Shah, Panchal and Wahash2, Reference Ahmad, Zada and Wang4, Reference Mali, Kucche and Costa Sousa24].
$\varphi $
-Hilfer FD framework became recently crucial, for more background, see [Reference Abdo, Shah, Panchal and Wahash2, Reference Ahmad, Zada and Wang4, Reference Mali, Kucche and Costa Sousa24].
This study investigates the following system:
 $$ \begin{align} \left\{\hspace{-3.5pt}\begin{array}{l} { }^{H} \mathcal{D}_{a^+}^{\alpha_1, \beta_1; \varphi} y_1(t)= g_1(t,y_1(t),y_2(t)), \quad t\in I' := (a, b],\\[0.3cm] { }^{H} \mathcal{D}_{a^+}^{\alpha_2, \beta_2; \varphi} y_2(t)= g_2(t,y_1(t),y_2(t)),\hspace{7pt} t \in I' := (a, b], \\[0.3cm] \lim_{t\to a^+} \! \varphi(t,a)^{1-\gamma_1} y_1(t) = \xi_1,\\[0.3cm] \lim_{t\to a^+} \! \varphi(t,a)^{1-\gamma_2} y_2(t) = \xi_2, \\ \end{array} \right. \end{align} $$
$$ \begin{align} \left\{\hspace{-3.5pt}\begin{array}{l} { }^{H} \mathcal{D}_{a^+}^{\alpha_1, \beta_1; \varphi} y_1(t)= g_1(t,y_1(t),y_2(t)), \quad t\in I' := (a, b],\\[0.3cm] { }^{H} \mathcal{D}_{a^+}^{\alpha_2, \beta_2; \varphi} y_2(t)= g_2(t,y_1(t),y_2(t)),\hspace{7pt} t \in I' := (a, b], \\[0.3cm] \lim_{t\to a^+} \! \varphi(t,a)^{1-\gamma_1} y_1(t) = \xi_1,\\[0.3cm] \lim_{t\to a^+} \! \varphi(t,a)^{1-\gamma_2} y_2(t) = \xi_2, \\ \end{array} \right. \end{align} $$
where
![]() ${}^{H}\mathcal {D}^{\alpha _i,\beta _i;\varphi }_{a^+}$
(for
${}^{H}\mathcal {D}^{\alpha _i,\beta _i;\varphi }_{a^+}$
(for
![]() $i=1,2$
) denotes the
$i=1,2$
) denotes the
![]() $\varphi $
-Hilfer FD of order
$\varphi $
-Hilfer FD of order
![]() $0<\alpha _i<1$
and type
$0<\alpha _i<1$
and type
![]() $0\leq \beta _i\leq 1$
,
$0\leq \beta _i\leq 1$
,
![]() $0<\gamma _i=\alpha _i+\beta _i(1-\alpha _i) <1$
,
$0<\gamma _i=\alpha _i+\beta _i(1-\alpha _i) <1$
,
![]() $1-\max _{1\leq i\leq 2}\{\gamma _i\}< \alpha _i -\mu _i $
,
$1-\max _{1\leq i\leq 2}\{\gamma _i\}< \alpha _i -\mu _i $
,
![]() $0<\mu _i<\alpha _i$
,
$0<\mu _i<\alpha _i$
,
![]() $(\mathbb {E},\|\cdot \|)$
is a Banach space and
$(\mathbb {E},\|\cdot \|)$
is a Banach space and
![]() $g_i : [a,b]\times \mathbb {E} \times \mathbb {E} \to \mathbb {E}$
(
$g_i : [a,b]\times \mathbb {E} \times \mathbb {E} \to \mathbb {E}$
(
![]() $i=1,2$
) satisfies some certain conditions, specified later,
$i=1,2$
) satisfies some certain conditions, specified later,
![]() $\xi _1,\xi _2 \in \mathbb {E}$
, and
$\xi _1,\xi _2 \in \mathbb {E}$
, and
![]() $ \varphi (t,a) =\varphi (t) -\varphi (a)$
, where
$ \varphi (t,a) =\varphi (t) -\varphi (a)$
, where
![]() $\varphi $
be increasing and differentiable with
$\varphi $
be increasing and differentiable with
![]() $\varphi ^{\prime }(t) \not = 0$
, for all
$\varphi ^{\prime }(t) \not = 0$
, for all
![]() $t \in [a,b]$
.
$t \in [a,b]$
.
In [Reference Almalahi and Panchal6, Reference Kharade and Kucche19, Reference Zhou, Wang and Zhang37], the authors investigated some classes of coupled systems in the frame of
![]() $\varphi $
-Hilfer FD. They obtained some quantitative and qualitative results by means of some classical fixed point theorems where the Lipschitz condition on the considered system is required. The proof of our existence theorem combines results from measure of noncompactness (MNC) and Darbo’s fixed point theorem under fairly reasonable assumptions on the forcing terms taking values on infinite-dimensional Banach space. Some interesting features of this work are as follows:
$\varphi $
-Hilfer FD. They obtained some quantitative and qualitative results by means of some classical fixed point theorems where the Lipschitz condition on the considered system is required. The proof of our existence theorem combines results from measure of noncompactness (MNC) and Darbo’s fixed point theorem under fairly reasonable assumptions on the forcing terms taking values on infinite-dimensional Banach space. Some interesting features of this work are as follows:
-
• The MNC expression is rigorously characterized in the functional space on which we work, allowing us to provide a unified approach for treating various differential systems regardless of the kind of the singularity generated by the initial condition.
-
• Under rather general assumptions, namely, when the nonlinearities fulfill an
 $L^{p} $
-Carathéodory type condition, a new existence criterion is proved.
$L^{p} $
-Carathéodory type condition, a new existence criterion is proved. -
• The results obtained in this work extend, refine, and generalize various related results appearing in the literature (see [Reference Derbazi and Baitiche13, Reference Derbazi, Baitiche, Benchohra and Graef14, Reference Vanterler da C. Sousa and Capelas de Oliveira32]).
-
• An illustrative example is discussed to show the applicability of our abstract results in treating differential systems in infinite-dimensional spaces driven by fractional derivatives [Reference Mursaleen25].
This work is divided into three sections. Section 2 recalls some theoretical concepts which are used throughout this work. In particular, a reconstruction of the MNC in a suitably selected Banach space is established. A new existence result is stated and demonstrated in Section 3. The last section provides an example illustrating the validity of our results.
2 Preliminary results
Let
![]() $I:=[a,b]$
. Throughout this work,
$I:=[a,b]$
. Throughout this work,
![]() $C(I,\mathbb {E})$
denotes all
$C(I,\mathbb {E})$
denotes all
![]() $\mathbb {E}$
-valued continuous functions on I with the sup norm
$\mathbb {E}$
-valued continuous functions on I with the sup norm
We endow the space
![]() $L^{p}_{\varphi }(I,{\mathbb {E}})$
,
$L^{p}_{\varphi }(I,{\mathbb {E}})$
,
![]() $1\leq p<\infty $
, of Bochner integrable functions z on I for which
$1\leq p<\infty $
, of Bochner integrable functions z on I for which
![]() $\|z\|_{L^p_{\varphi }}< \infty $
, with the norm
$\|z\|_{L^p_{\varphi }}< \infty $
, with the norm
 $\|z\|_{L^p_{\varphi }} =\left (\displaystyle \int _a^b \varphi '(s)\| z(s)\|^p d s \right )^{\frac {1}{p}}$
. If
$\|z\|_{L^p_{\varphi }} =\left (\displaystyle \int _a^b \varphi '(s)\| z(s)\|^p d s \right )^{\frac {1}{p}}$
. If
![]() $\varphi (t)=t$
, the space
$\varphi (t)=t$
, the space
![]() $L^{p}_{\varphi }(I,\mathbb {E})$
coincides with the usual
$L^{p}_{\varphi }(I,\mathbb {E})$
coincides with the usual
![]() $L^{p}(I,\mathbb {E})$
space.
$L^{p}(I,\mathbb {E})$
space.
If
![]() $p=\infty $
,
$p=\infty $
,
![]() $L^{\infty }(I,\mathbb {E})$
is the Banach space of all equivalence classes of essentially bounded measurable functions on I equipped with the norm
$L^{\infty }(I,\mathbb {E})$
is the Banach space of all equivalence classes of essentially bounded measurable functions on I equipped with the norm
We also define
For
![]() $ \varphi \in \mathbb {S}_{a^+}^{1,+}(I, \mathbb {R}) $
and
$ \varphi \in \mathbb {S}_{a^+}^{1,+}(I, \mathbb {R}) $
and
![]() $t, s \in I$
,
$t, s \in I$
,
![]() $(t> s)$
, we pose
$(t> s)$
, we pose
Definition 2.1 [Reference Diaz and Teruel15]
For
![]() $ \alpha , \beta \in (0,+\infty ) $
, the gamma and beta functions are given by
$ \alpha , \beta \in (0,+\infty ) $
, the gamma and beta functions are given by
Lemma 2.2 [Reference Nguyen26]
Let
![]() $\psi \in \mathbb {S}_{a^+}^{1,+}(I, \mathbb {R})$
,
$\psi \in \mathbb {S}_{a^+}^{1,+}(I, \mathbb {R})$
,
![]() $0< \alpha < 1$
,
$0< \alpha < 1$
,
![]() $0\leqslant \beta < \alpha $
,
$0\leqslant \beta < \alpha $
,
![]() $a \leq \tau \leq \zeta \leq t \leq b$
, and let
$a \leq \tau \leq \zeta \leq t \leq b$
, and let
Then, for all
![]() $t \in I $
, we have
$t \in I $
, we have
and
 $$ \begin{align*}0 \leq \Theta_{\alpha,\beta}(\tau,\zeta,t,\varphi) \leq \left( \frac{2^{\beta}}{\alpha} + \frac{2^{1-\alpha}}{1-\beta} \right) \max\{1, \varphi(b,a)^{\alpha -\beta}\}\varphi(\zeta,\tau)^{\min\{\alpha,1-\beta,\alpha -\beta\} }. \end{align*} $$
$$ \begin{align*}0 \leq \Theta_{\alpha,\beta}(\tau,\zeta,t,\varphi) \leq \left( \frac{2^{\beta}}{\alpha} + \frac{2^{1-\alpha}}{1-\beta} \right) \max\{1, \varphi(b,a)^{\alpha -\beta}\}\varphi(\zeta,\tau)^{\min\{\alpha,1-\beta,\alpha -\beta\} }. \end{align*} $$
Remark 2.3 [Reference Nguyen26]
From Lemma 2.2, one has:
-
(i)
 $\Theta _{\alpha ,\beta }(a,t,t,\varphi ) \leq \Theta _{\alpha ,\beta }(a,b,b,\varphi ) $
for
$\Theta _{\alpha ,\beta }(a,t,t,\varphi ) \leq \Theta _{\alpha ,\beta }(a,b,b,\varphi ) $
for
 $t\in I$
,
$t\in I$
, -
(ii)
 $\Theta _{\alpha ,\beta }(\tau ,\zeta ,t,\varphi )\to 0$
as
$\Theta _{\alpha ,\beta }(\tau ,\zeta ,t,\varphi )\to 0$
as
 $|\zeta -\tau |\to 0$
.
$|\zeta -\tau |\to 0$
.
Remark 2.4 By Lemma 2.2, we get
So it is possible to choose
![]() $\aleph $
such that
$\aleph $
such that
 $$ \begin{align} \mathcal{L}_{i,j}(\aleph) &:= \sup_{t \in I} \frac{2 \Vert \eta_{i,j} \Vert_{L^{\infty}}\varphi(b,a)^{1- \gamma_i }}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{-\aleph (t-s)} ds \\[0.2cm] & <1/4.\nonumber \end{align} $$
$$ \begin{align} \mathcal{L}_{i,j}(\aleph) &:= \sup_{t \in I} \frac{2 \Vert \eta_{i,j} \Vert_{L^{\infty}}\varphi(b,a)^{1- \gamma_i }}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{-\aleph (t-s)} ds \\[0.2cm] & <1/4.\nonumber \end{align} $$
Definition 2.5 The left-sided
![]() $\varphi $
-fractional integral of a function f of order
$\varphi $
-fractional integral of a function f of order
![]() $\alpha>0$
is defined as
$\alpha>0$
is defined as
with
![]() $\varphi \in \mathbb {S}_{a^+}^{1,+}(I,\mathbb {R})$
.
$\varphi \in \mathbb {S}_{a^+}^{1,+}(I,\mathbb {R})$
.
Definition 2.6 Let
![]() $ n-1 <\alpha \leq n $
with
$ n-1 <\alpha \leq n $
with
![]() $ n\in \mathbb {N}$
,
$ n\in \mathbb {N}$
,
![]() $ \varphi \in \mathbb {S}_{a^+}^{1,+}(I,\mathbb {R})$
. The left-sided
$ \varphi \in \mathbb {S}_{a^+}^{1,+}(I,\mathbb {R})$
. The left-sided
![]() $\varphi $
-Hilfer FD of a function f of order
$\varphi $
-Hilfer FD of a function f of order
![]() $\alpha $
and type
$\alpha $
and type
![]() $ 0\leq \beta \leq 1$
is defined as
$ 0\leq \beta \leq 1$
is defined as
 $$ \begin{align*} \left({^{H}} {\mathcal{D}}_{a^+}^{\alpha, \beta;\varphi} f\right)(t) =\left( \mathcal{I}_{a^+}^{\beta(n-\alpha),\varphi}\left(\frac{1}{\varphi^{\prime}(t)} \frac{d}{d t}\right)^n \left( \mathcal{I}_{a^+}^{(1-\beta)(n-\alpha ),\varphi} f \right)\right)(t). \end{align*} $$
$$ \begin{align*} \left({^{H}} {\mathcal{D}}_{a^+}^{\alpha, \beta;\varphi} f\right)(t) =\left( \mathcal{I}_{a^+}^{\beta(n-\alpha),\varphi}\left(\frac{1}{\varphi^{\prime}(t)} \frac{d}{d t}\right)^n \left( \mathcal{I}_{a^+}^{(1-\beta)(n-\alpha ),\varphi} f \right)\right)(t). \end{align*} $$
To define a solution of the system (1.1), for each
![]() $i=1,2$
, we consider the Banach space
$i=1,2$
, we consider the Banach space
normed by
Also, by
![]() $\mathcal {C}_{1-\gamma _1}^{\varphi } (I,\mathbb {E}) \times \mathcal {C}_{1-\gamma _2}^{\varphi } (I,\mathbb {E})$
we denote the product weighted space with the norm
$\mathcal {C}_{1-\gamma _1}^{\varphi } (I,\mathbb {E}) \times \mathcal {C}_{1-\gamma _2}^{\varphi } (I,\mathbb {E})$
we denote the product weighted space with the norm
Henceforth, for a subset
![]() $\mathbb {U}$
of the space
$\mathbb {U}$
of the space
![]() $\mathcal {C}_{1-\gamma _i}^{\varphi }(I,\mathbb {E})$
, define
$\mathcal {C}_{1-\gamma _i}^{\varphi }(I,\mathbb {E})$
, define
![]() $\mathbb {U}_{\gamma _i}$
by
$\mathbb {U}_{\gamma _i}$
by
where
 $$ \begin{align} z_{\gamma_i}(t) =\left\{\hspace{-4pt}\begin{array}{l} \varphi(t,a)^{1-\gamma_i} z(t),\quad t\in I',\\[0.3cm] \lim_{t\to a^{+}} \varphi(t,a)^{1-\gamma_i} z(t),\quad t=a. \end{array} \right. \end{align} $$
$$ \begin{align} z_{\gamma_i}(t) =\left\{\hspace{-4pt}\begin{array}{l} \varphi(t,a)^{1-\gamma_i} z(t),\quad t\in I',\\[0.3cm] \lim_{t\to a^{+}} \varphi(t,a)^{1-\gamma_i} z(t),\quad t=a. \end{array} \right. \end{align} $$
It is clear that
![]() $z_{\gamma _i}\in C(I,\mathbb {E})$
.
$z_{\gamma _i}\in C(I,\mathbb {E})$
.
Definition 2.7 [Reference Banas and Goebel10]
The Hausdorff MNC is the map
![]() $\Lambda : \mathcal {P}(\mathbb {E}) \to [0,\infty )$
defined by
$\Lambda : \mathcal {P}(\mathbb {E}) \to [0,\infty )$
defined by
where
![]() $\mathcal {P}(\mathbb {E})$
denotes the family of all bounded subsets of
$\mathcal {P}(\mathbb {E})$
denotes the family of all bounded subsets of
![]() $\mathbb {E}$
.
$\mathbb {E}$
.
Lemma 2.8 [Reference Banas and Goebel10]
Let
![]() $\mathbb {E}$
be a real Banach space and
$\mathbb {E}$
be a real Banach space and
![]() $\mathbb {U}_0, \mathbb {U}_1, \mathbb {U}_2 \in \mathcal {P}(\mathbb {E})$
. Then the following properties are satisfied:
$\mathbb {U}_0, \mathbb {U}_1, \mathbb {U}_2 \in \mathcal {P}(\mathbb {E})$
. Then the following properties are satisfied:
-
(1)
 $\Lambda \left (\mathbb {U}_{0}\right ) \leq \Lambda \left (\mathbb {U}_{1}\right )$
if
$\Lambda \left (\mathbb {U}_{0}\right ) \leq \Lambda \left (\mathbb {U}_{1}\right )$
if
 $ \mathbb {U}_{0} \subset \mathbb {U}_{1}$
,
$ \mathbb {U}_{0} \subset \mathbb {U}_{1}$
, -
(2)
 $\Lambda (\{a\} \cup \mathbb {U})=\Lambda (\mathbb {U})$
for every
$\Lambda (\{a\} \cup \mathbb {U})=\Lambda (\mathbb {U})$
for every
 $a \in \mathbb {E}$
,
$a \in \mathbb {E}$
, -
(4)
 $\Lambda (\mathbb {U}) =\Lambda (\operatorname {\overline {conv}}\mathbb {U}) $
, where
$\Lambda (\mathbb {U}) =\Lambda (\operatorname {\overline {conv}}\mathbb {U}) $
, where
 $\operatorname {\overline {conv}} \mathbb {U} $
is the closed convex hull of
$\operatorname {\overline {conv}} \mathbb {U} $
is the closed convex hull of
 $\mathbb {U}$
,
$\mathbb {U}$
, -
(4)
 $\Lambda (\mu \mathbb {U})= |\mu |\Lambda ( \mathbb {U}), $
where
$\Lambda (\mu \mathbb {U})= |\mu |\Lambda ( \mathbb {U}), $
where
 $\mu \in \mathbb {R}$
,
$\mu \in \mathbb {R}$
, -
(5)
 $\Lambda (\mathbb {U})=0$
if and only if
$\Lambda (\mathbb {U})=0$
if and only if
 $\mathbb {U}$
is relatively compact,
$\mathbb {U}$
is relatively compact, -
(6)
 $\Lambda \left (\mathbb {U}_{2} \cup \mathbb {U}_{1}\right )=\max \left (\Lambda \left (\mathbb {U}_{2}\right ), \Lambda \left (\mathbb {U}_{1}\right )\right )$
,
$\Lambda \left (\mathbb {U}_{2} \cup \mathbb {U}_{1}\right )=\max \left (\Lambda \left (\mathbb {U}_{2}\right ), \Lambda \left (\mathbb {U}_{1}\right )\right )$
, -
(7)
 $\Lambda \left (\mathbb {U}_{2} + \mathbb {U}_{1}\right )\leq \Lambda \left (\mathbb {U}_{2}\right ) +\Lambda \left (\mathbb {U}_{1}\right )$
.
$\Lambda \left (\mathbb {U}_{2} + \mathbb {U}_{1}\right )\leq \Lambda \left (\mathbb {U}_{2}\right ) +\Lambda \left (\mathbb {U}_{1}\right )$
.
Lemma 2.9 [Reference Banas and Goebel11]
Let
![]() $\mathbb {B}\subseteq C(I, \mathbb {E})$
be a bounded set. Then, for all
$\mathbb {B}\subseteq C(I, \mathbb {E})$
be a bounded set. Then, for all
![]() $t\in I$
,
$t\in I$
,
where
![]() $\mathbb {B}(t)=\{u(t)\,:\, u\in \mathbb {B}\}$
. Furthermore, if
$\mathbb {B}(t)=\{u(t)\,:\, u\in \mathbb {B}\}$
. Furthermore, if
![]() $\mathbb {B}$
is equicontinuous on I, then
$\mathbb {B}$
is equicontinuous on I, then
![]() $\Lambda (\mathbb {B}(\cdot ))$
is continuous on I and
$\Lambda (\mathbb {B}(\cdot ))$
is continuous on I and
where
![]() $\Lambda _c$
is the Hausdorff MNC in
$\Lambda _c$
is the Hausdorff MNC in
![]() $C(I, \mathbb {E})$
.
$C(I, \mathbb {E})$
.
Next, we extend the result of Lemma 2.9 to the space
![]() $\mathcal {C}_{1-\gamma }^{\varphi } (I,\mathbb {E})$
. Let us confirm that, in general, the expression (2.4) may not be well-defined, since bounded sets in
$\mathcal {C}_{1-\gamma }^{\varphi } (I,\mathbb {E})$
. Let us confirm that, in general, the expression (2.4) may not be well-defined, since bounded sets in
![]() $\mathcal {C}_{1-\gamma }^{\varphi } (I,\mathbb {E})$
are not necessarily bounded in
$\mathcal {C}_{1-\gamma }^{\varphi } (I,\mathbb {E})$
are not necessarily bounded in
![]() $C(I,\mathbb {E})$
. Consider, for instance, the set
$C(I,\mathbb {E})$
. Consider, for instance, the set
where
![]() $\mathcal {Q}$
is bounded in
$\mathcal {Q}$
is bounded in
![]() $C(I,\mathbb {E})$
. Obviously,
$C(I,\mathbb {E})$
. Obviously,
![]() $\widetilde {\mathcal {Q}}$
is unbounded in
$\widetilde {\mathcal {Q}}$
is unbounded in
![]() $C(I,\mathbb {E})$
, this indicates that the map
$C(I,\mathbb {E})$
, this indicates that the map
![]() $t\mapsto \Lambda (\widetilde {\mathcal {Q}}(t))$
is not well-defined, therefore it is wrong to consider the expression (2.4). However, clearly the set
$t\mapsto \Lambda (\widetilde {\mathcal {Q}}(t))$
is not well-defined, therefore it is wrong to consider the expression (2.4). However, clearly the set
![]() $\widetilde {\mathcal {Q}}$
is bounded with respect to the norm (2.2) (i.e.,
$\widetilde {\mathcal {Q}}$
is bounded with respect to the norm (2.2) (i.e.,
![]() $\widetilde {\mathcal {Q}}\subset \mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E})$
).
$\widetilde {\mathcal {Q}}\subset \mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E})$
).
Lemma 2.10 Let
![]() $\mathbb {B} \subseteq \mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E})$
be a bounded set. Then, for all
$\mathbb {B} \subseteq \mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E})$
be a bounded set. Then, for all
![]() $t\in I$
, we have
$t\in I$
, we have
Additionally, assume that
![]() $\mathbb {B}$
is equicontinuous on I, then
$\mathbb {B}$
is equicontinuous on I, then
![]() $\Lambda (\mathbb {B}_\gamma (\cdot ))$
is continuous on I and
$\Lambda (\mathbb {B}_\gamma (\cdot ))$
is continuous on I and
Proof For every
![]() $\epsilon>0$
, there exists
$\epsilon>0$
, there exists
![]() $\mathbb {B}_i \subseteq \mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E})$
, (
$\mathbb {B}_i \subseteq \mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E})$
, (
![]() $i=1,\dots ,n$
) such that
$i=1,\dots ,n$
) such that
![]() ${\mathbb {B}=\displaystyle\bigcup\limits _{i=1}^{n}\mathbb {B}_i}$
and
${\mathbb {B}=\displaystyle\bigcup\limits _{i=1}^{n}\mathbb {B}_i}$
and
where
![]() $\delta (\cdot )$
denotes the diameter of a bounded set in
$\delta (\cdot )$
denotes the diameter of a bounded set in
![]() $\mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E})$
. So, we have
$\mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E})$
. So, we have
and
From (2.5) and (2.6), it follows that
Since
![]() $\epsilon $
is arbitrary, one has
$\epsilon $
is arbitrary, one has
Consequently, we have
Now, let us prove the converse inequality. Assume that
![]() $\mathbb {B}$
is a bounded subset in
$\mathbb {B}$
is a bounded subset in
![]() $\mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E})$
and equicontinuous on I. Obviously,
$\mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E})$
and equicontinuous on I. Obviously,
![]() $\mathbb {B}_\gamma $
is a bounded subset in
$\mathbb {B}_\gamma $
is a bounded subset in
![]() $C(I,\mathbb {E})$
and equicontinuous on I. From Lemma 2.9, we obtain that
$C(I,\mathbb {E})$
and equicontinuous on I. From Lemma 2.9, we obtain that
Consider the isometric map
![]() $ \Upsilon : \mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E}) \to C(I,\mathbb {E})$
defined by
$ \Upsilon : \mathcal {C}_{1-\gamma }^{\varphi }(I,\mathbb {E}) \to C(I,\mathbb {E})$
defined by
![]() $z \mapsto z_\gamma $
. Then, we get
$z \mapsto z_\gamma $
. Then, we get
and the result is reached.
Lemma 2.11 [Reference Kamenskii, Obukhovskii and Zecca18]
Let
![]() $\{x_n\}_{n=1}^{+\infty }$
belongs to
$\{x_n\}_{n=1}^{+\infty }$
belongs to
![]() $L^{1}(I,\mathbb {E})$
such that
$L^{1}(I,\mathbb {E})$
such that
![]() $\|x_n(t)\|\leq \varsigma (t)$
almost everywhere on
$\|x_n(t)\|\leq \varsigma (t)$
almost everywhere on
![]() $I (n=1,2,\dots )$
for some
$I (n=1,2,\dots )$
for some
![]() $\varsigma \in L^{1}(I,\mathbb {R}_+)$
. Then, the map
$\varsigma \in L^{1}(I,\mathbb {R}_+)$
. Then, the map
![]() $t\mapsto \Lambda (\{x_n(t)\}_{n=1}^{+\infty })$
is integrable on
$t\mapsto \Lambda (\{x_n(t)\}_{n=1}^{+\infty })$
is integrable on
![]() $\mathbb {R}_+$
and
$\mathbb {R}_+$
and
 $$ \begin{align} \Lambda\left(\left\{\int_0^t x_n(s)ds\ \right\}_{n=1}^{+\infty} \right) \leq 2\int_0^t \Lambda(\{x_n(s) \}_{n=1}^{+\infty})ds. \end{align} $$
$$ \begin{align} \Lambda\left(\left\{\int_0^t x_n(s)ds\ \right\}_{n=1}^{+\infty} \right) \leq 2\int_0^t \Lambda(\{x_n(s) \}_{n=1}^{+\infty})ds. \end{align} $$
Lemma 2.12 [Reference Aghajani and Sabzali3]
Let
![]() $\mathbb {B}\in \mathcal {P}(\mathbb {E})$
. Then for each
$\mathbb {B}\in \mathcal {P}(\mathbb {E})$
. Then for each
![]() $\epsilon> 0$
, there exists a sequence
$\epsilon> 0$
, there exists a sequence
![]() $\{x_n\}_{n=1}^{+\infty }\subseteq \mathbb {B}$
, satisfies
$\{x_n\}_{n=1}^{+\infty }\subseteq \mathbb {B}$
, satisfies
Theorem 2.13 (Darbo[Reference Darbo12])
Let
![]() $\mathbb {E}$
be a Banach space, let
$\mathbb {E}$
be a Banach space, let
![]() $\mathbb {V}\subset \mathbb {E}$
be a nonempty, bounded, closed, convex, and let
$\mathbb {V}\subset \mathbb {E}$
be a nonempty, bounded, closed, convex, and let
![]() $N: \mathbb {V} \rightarrow \mathbb {V}$
be a continuous mapping. Assume that there exists
$N: \mathbb {V} \rightarrow \mathbb {V}$
be a continuous mapping. Assume that there exists
![]() $k \in [0,1)$
such that
$k \in [0,1)$
such that
Then N admits a fixed point in
![]() $\mathbb {V}$
.
$\mathbb {V}$
.
Theorem 2.14 [Reference Banas and Goebel10]
Suppose
![]() $\varpi _1,\varpi _2,\dots ,\varpi _n$
are MNCs in the Banach spaces
$\varpi _1,\varpi _2,\dots ,\varpi _n$
are MNCs in the Banach spaces
![]() $\mathbb {E}_1,\mathbb {E}_2,\dots ,\mathbb {E}_n$
, respectively. Let
$\mathbb {E}_1,\mathbb {E}_2,\dots ,\mathbb {E}_n$
, respectively. Let
![]() $G : [0,\infty )^{n} \to [0,\infty ) $
be a convex function such that
$G : [0,\infty )^{n} \to [0,\infty ) $
be a convex function such that
![]() $G(x_1,x_2,\dots ,x_n) =0 $
if and only if
$G(x_1,x_2,\dots ,x_n) =0 $
if and only if
![]() $x_i = 0$
for
$x_i = 0$
for
![]() $i=1,2,\dots ,n$
. Then
$i=1,2,\dots ,n$
. Then
defines an MNC in
![]() $\mathbb {E}_1 \times \mathbb {E}_2 \times \dots \times \mathbb {E}_n$
, where
$\mathbb {E}_1 \times \mathbb {E}_2 \times \dots \times \mathbb {E}_n$
, where
![]() $X_i$
denotes the natural projection of X into
$X_i$
denotes the natural projection of X into
![]() $\mathbb {E}_i$
for
$\mathbb {E}_i$
for
![]() $i=1,2,\dots ,n$
.
$i=1,2,\dots ,n$
.
Example 2.15 Let
![]() $\varpi _1,\varpi _2 $
be MNCs in
$\varpi _1,\varpi _2 $
be MNCs in
![]() $\mathbb {E}_1, \mathbb {E}_2$
, respectively and
$\mathbb {E}_1, \mathbb {E}_2$
, respectively and
![]() $G(x_1,x_2) = x_1 + x_2 $
for
$G(x_1,x_2) = x_1 + x_2 $
for
![]() $(x_1,x_2) \in [0,\infty )^{2}$
. Then, G satisfies all properties of Theorem 2.14. Hence,
$(x_1,x_2) \in [0,\infty )^{2}$
. Then, G satisfies all properties of Theorem 2.14. Hence,
![]() $ \varpi (X) = \varpi _1(X_1) +\varpi _2(X_2) $
is an MNC in the space
$ \varpi (X) = \varpi _1(X_1) +\varpi _2(X_2) $
is an MNC in the space
![]() $\mathbb {E}_1\times \mathbb {E}_2$
.
$\mathbb {E}_1\times \mathbb {E}_2$
.
3 Main results
We initiate this section by introducing the following hypotheses which are needed in the sequel:
-
(H1) The functions
 $t\mapsto g_i(t,u,v); i=1,2$
are measurable on I for each
$t\mapsto g_i(t,u,v); i=1,2$
are measurable on I for each
 $(u,v)\in C(I, \mathbb {E})\times C(I, \mathbb {E})$
, and the functions
$(u,v)\in C(I, \mathbb {E})\times C(I, \mathbb {E})$
, and the functions
 $(u,v) \mapsto g_i(t,u,v)$
are continuous for a.e.
$(u,v) \mapsto g_i(t,u,v)$
are continuous for a.e.
 $t \in I$
.
$t \in I$
. -
(H2) There exist functions
 $h_i\in L^{\frac {1}{\mu _i}}_{\varphi }(I,\mathbb {R}_+)$
,
$h_i\in L^{\frac {1}{\mu _i}}_{\varphi }(I,\mathbb {R}_+)$
,
 $0\leq \mu _i <\alpha _i $
such that for
$0\leq \mu _i <\alpha _i $
such that for $$ \begin{align*}\|g_i(t,v_1,v_2)\|\leq h_i(t) \left( 1 + \|v_1\| + \|v_2\| \right),\quad i=1,2, \end{align*} $$
$$ \begin{align*}\|g_i(t,v_1,v_2)\|\leq h_i(t) \left( 1 + \|v_1\| + \|v_2\| \right),\quad i=1,2, \end{align*} $$
 $v_1, v_2 \in \mathbb {E}$
, and a.e.
$v_1, v_2 \in \mathbb {E}$
, and a.e.
 $t\in I$
.
$t\in I$
.
-
(H3) There exist functions
 $\eta _i, \widehat {\eta }_i \in L^\infty (I,\mathbb {R}_+)$
,
$\eta _i, \widehat {\eta }_i \in L^\infty (I,\mathbb {R}_+)$
,
 $i = 1,2$
, such that for any bounded subsets
$i = 1,2$
, such that for any bounded subsets
 $\mathbb {A}^1\times \mathbb {A}^2\subset \mathcal {C}_{1-\gamma _1}^{\varphi }(I,\mathbb {E})\times \mathcal {C}_{1-\gamma _2}^{\varphi }(I,\mathbb {E})$
, we have (3.1)
$\mathbb {A}^1\times \mathbb {A}^2\subset \mathcal {C}_{1-\gamma _1}^{\varphi }(I,\mathbb {E})\times \mathcal {C}_{1-\gamma _2}^{\varphi }(I,\mathbb {E})$
, we have (3.1) $$ \begin{align} \Lambda(g_i(t,\mathbb{A}^1,\mathbb{A}^2)) \leq \displaystyle\sum_{j=1}^{2} \eta_{i,j}(t) \Lambda(\mathbb{A}^j) ,\quad \text{for all}~~ t\in I. \end{align} $$
$$ \begin{align} \Lambda(g_i(t,\mathbb{A}^1,\mathbb{A}^2)) \leq \displaystyle\sum_{j=1}^{2} \eta_{i,j}(t) \Lambda(\mathbb{A}^j) ,\quad \text{for all}~~ t\in I. \end{align} $$
-
(H4) The following inequality holds:
(3.2)where $$ \begin{align} 2 \widehat{K}_i\leq K,\quad i=1,2, \end{align} $$
$$ \begin{align} 2 \widehat{K}_i\leq K,\quad i=1,2, \end{align} $$
 $$ \begin{align*} K_i &:= \| \xi_i\| + \frac{ \varphi(b,a)^{1 + \alpha_i - \gamma_i -\mu_i }\Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}}}{\Gamma(\alpha_i) \theta_{i}^{1-\mu_i}} \\[4pt] &\qquad \qquad + K \displaystyle\sum_{j=1}^{2}\frac{\varphi(b,a)^{1-\gamma_i} \Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}} }{\Gamma(\alpha_i)} \left( \Theta_{\theta_i, \vartheta_{i,j}} (a,b,b,\varphi) \right)^{1-\mu_i}, \end{align*} $$
$$ \begin{align*} K_i &:= \| \xi_i\| + \frac{ \varphi(b,a)^{1 + \alpha_i - \gamma_i -\mu_i }\Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}}}{\Gamma(\alpha_i) \theta_{i}^{1-\mu_i}} \\[4pt] &\qquad \qquad + K \displaystyle\sum_{j=1}^{2}\frac{\varphi(b,a)^{1-\gamma_i} \Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}} }{\Gamma(\alpha_i)} \left( \Theta_{\theta_i, \vartheta_{i,j}} (a,b,b,\varphi) \right)^{1-\mu_i}, \end{align*} $$
 $$ \begin{align*}\theta_i = \frac{\alpha_i -\mu_i}{1-\mu_i},\quad \text{and}\quad \vartheta_{i,j} =\frac{1 -\gamma_{j}}{1-\mu_i},\quad i,j=1,2. \end{align*} $$
$$ \begin{align*}\theta_i = \frac{\alpha_i -\mu_i}{1-\mu_i},\quad \text{and}\quad \vartheta_{i,j} =\frac{1 -\gamma_{j}}{1-\mu_i},\quad i,j=1,2. \end{align*} $$
Now, we prove our main result for the system (1.1), which is based on Theorem 2.13.
Theorem 3.1 Assume that (H1)–(H4) hold. Then, system (1.1) has at least one solution.
Proof First, let us introduce an operator
![]() $\mathcal {H}: \mathcal {C}_{1-\gamma _1}^{\varphi }(I,\mathbb {E})\times \mathcal {C}_{1-\gamma _2}^{\varphi }(I,\mathbb {E}) \to \mathcal {C}_{1-\gamma _1}^{\varphi }(I,\mathbb {E})\times \mathcal {C}_{1-\gamma _2}^{\varphi }(I,\mathbb {E})$
associated with the system (1.1) as
$\mathcal {H}: \mathcal {C}_{1-\gamma _1}^{\varphi }(I,\mathbb {E})\times \mathcal {C}_{1-\gamma _2}^{\varphi }(I,\mathbb {E}) \to \mathcal {C}_{1-\gamma _1}^{\varphi }(I,\mathbb {E})\times \mathcal {C}_{1-\gamma _2}^{\varphi }(I,\mathbb {E})$
associated with the system (1.1) as
where the operators
![]() $\mathcal {H}_i:\mathcal {C}_{1-\gamma _1}^{\varphi }(I,\mathbb {E})\times \mathcal {C}_{1-\gamma _2}^{\varphi }(I,\mathbb {E}) \to \mathcal {C}_{1-\gamma _i}^{\varphi }(I,\mathbb {E})$
,
$\mathcal {H}_i:\mathcal {C}_{1-\gamma _1}^{\varphi }(I,\mathbb {E})\times \mathcal {C}_{1-\gamma _2}^{\varphi }(I,\mathbb {E}) \to \mathcal {C}_{1-\gamma _i}^{\varphi }(I,\mathbb {E})$
,
![]() $i=1,2$
are defined by
$i=1,2$
are defined by
According to [Reference Kucche and Mali22, Lemma 3.1], the solutions of the system (1.1) are fixed points of the operator
![]() $\mathcal {H}$
. Consider the following bounded closed convex set:
$\mathcal {H}$
. Consider the following bounded closed convex set:
Then we divide the proof into four steps.
Step 1.
![]() $\mathcal {H}$
transforms
$\mathcal {H}$
transforms
![]() $\Omega _{K}$
into itself. Indeed, for each
$\Omega _{K}$
into itself. Indeed, for each
![]() $(y_1,y_2)\in \Omega _{K}$
and every
$(y_1,y_2)\in \Omega _{K}$
and every
![]() $t\in I'$
, one has
$t\in I'$
, one has
 $$ \begin{align*} & \left\| \varphi(t,a)^{1-\gamma_i} \left( \mathcal{H}_i(y_1,y_2)\right)(t)\right\| \\[5pt] &\leq \| \xi_i\| + \frac{\varphi(t,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi'(s)\varphi(t,s)^{\alpha_i -1} \left\| g_i(s, y_1(s),y_2(s)) \right\|d s \\[5pt] &\leq \| \xi_i\| + \frac{\varphi(t,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi'(s)\varphi(t,s)^{\alpha_i -1} h_i(s) \left( 1 + \|y_1(s)\| + \|y_2(s)\| \right) d s \\[5pt] & \leq \| \xi_i\| + \frac{\varphi(t,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi'(s)\varphi(t,s)^{\alpha_i -1} h_i(s) (1+ \varphi(s,a)^{\gamma_1 -1}\|y_1\|_{\mathcal{C}_{1-\gamma_1}^{\varphi}} \\[5pt] & \qquad + \varphi(s,a)^{\gamma_2 -1}\|y_2\|_{\mathcal{C}_{1-\gamma_2}^{\varphi}} )ds \\[5pt] & \leq \| \xi_i\| + \frac{\varphi(t,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi(t,s)^{\alpha_i -1} h_i(s) \left(1 +K \displaystyle\sum_{j=1}^{2} \varphi(s,a)^{\gamma_{j} -1} \right) \varphi'(s) ds. \end{align*} $$
$$ \begin{align*} & \left\| \varphi(t,a)^{1-\gamma_i} \left( \mathcal{H}_i(y_1,y_2)\right)(t)\right\| \\[5pt] &\leq \| \xi_i\| + \frac{\varphi(t,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi'(s)\varphi(t,s)^{\alpha_i -1} \left\| g_i(s, y_1(s),y_2(s)) \right\|d s \\[5pt] &\leq \| \xi_i\| + \frac{\varphi(t,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi'(s)\varphi(t,s)^{\alpha_i -1} h_i(s) \left( 1 + \|y_1(s)\| + \|y_2(s)\| \right) d s \\[5pt] & \leq \| \xi_i\| + \frac{\varphi(t,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi'(s)\varphi(t,s)^{\alpha_i -1} h_i(s) (1+ \varphi(s,a)^{\gamma_1 -1}\|y_1\|_{\mathcal{C}_{1-\gamma_1}^{\varphi}} \\[5pt] & \qquad + \varphi(s,a)^{\gamma_2 -1}\|y_2\|_{\mathcal{C}_{1-\gamma_2}^{\varphi}} )ds \\[5pt] & \leq \| \xi_i\| + \frac{\varphi(t,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi(t,s)^{\alpha_i -1} h_i(s) \left(1 +K \displaystyle\sum_{j=1}^{2} \varphi(s,a)^{\gamma_{j} -1} \right) \varphi'(s) ds. \end{align*} $$
Since
![]() $\mu _i + (1- \mu _i)=1$
, we can write
$\mu _i + (1- \mu _i)=1$
, we can write
![]() $ \varphi '(s)$
as the product
$ \varphi '(s)$
as the product
Then, applying the Hölder inequality, we get
 $$ \begin{align*} &\hspace{-0.3cm} \left\| \varphi(t,a)^{1-\gamma_i} \left( \mathcal{H}_i(y_1,y_2)\right)(t)\right\|\\[5pt] & \leq \| \xi_i\| + \frac{\varphi(t,a)^{1-\gamma_i} \Vert h_i\Vert_{ L^{\frac{1}{\mu_i}}_{\varphi} } }{\Gamma(\alpha_i)}\left( \int_{a}^{t} \varphi(t,s)^{\frac{\alpha_i -1}{1-\mu_i}} d\varphi(s) \right)^{1-\mu_i} \\[5pt] & \quad + K \displaystyle\sum_{j=1}^{2} \frac{\varphi(t,a)^{1-\gamma_i} \Vert h_i\Vert_{ L^{\frac{1}{\mu_i}}_{\varphi} } }{\Gamma(\alpha_i)} \left( \int_{a}^{t} \varphi(t,s)^{\frac{\alpha_i -1}{1-\mu_i}} \varphi(s,a)^{\frac{\gamma_{j} -1}{1-\mu_i}} d\varphi(s) \right)^{1-\mu_i}. \end{align*} $$
$$ \begin{align*} &\hspace{-0.3cm} \left\| \varphi(t,a)^{1-\gamma_i} \left( \mathcal{H}_i(y_1,y_2)\right)(t)\right\|\\[5pt] & \leq \| \xi_i\| + \frac{\varphi(t,a)^{1-\gamma_i} \Vert h_i\Vert_{ L^{\frac{1}{\mu_i}}_{\varphi} } }{\Gamma(\alpha_i)}\left( \int_{a}^{t} \varphi(t,s)^{\frac{\alpha_i -1}{1-\mu_i}} d\varphi(s) \right)^{1-\mu_i} \\[5pt] & \quad + K \displaystyle\sum_{j=1}^{2} \frac{\varphi(t,a)^{1-\gamma_i} \Vert h_i\Vert_{ L^{\frac{1}{\mu_i}}_{\varphi} } }{\Gamma(\alpha_i)} \left( \int_{a}^{t} \varphi(t,s)^{\frac{\alpha_i -1}{1-\mu_i}} \varphi(s,a)^{\frac{\gamma_{j} -1}{1-\mu_i}} d\varphi(s) \right)^{1-\mu_i}. \end{align*} $$
Hence, by Lemma 2.2 and Remark 2.3, we obtain
 $$ \begin{align*} \left\|\varphi(t,a)^{1-\gamma_i} \left( \mathcal{H}_i(y_1,y_2)\right)(t)\right\| &\leq \| \xi_i\| + \frac{ \Vert h_i\Vert_{ L^{\frac{1}{\mu_i}}_{\varphi} } }{\Gamma(\alpha_i)} \left(\frac{1-\mu_i}{\alpha_i -\mu_i}\right)^{1-\mu_i}\varphi(t,a)^{1 + \alpha_i - \gamma_i -\mu_i } \\ &\quad + K \displaystyle\sum_{j=1}^{2}\frac{\varphi(t,a)^{1-\gamma_i} \Vert h_i\Vert_{ L^{\frac{1}{\mu_i}}_{\varphi} } }{\Gamma(\alpha_i)} \left( \Theta_{\frac{\alpha_i -\mu_i}{1-\mu_i}, \frac{1-\gamma_{j} }{1-\mu_i}} (a,t,t,\varphi) \right)^{1-\mu_i}\\ &\leq \widehat{K}_i,\quad i=1,2. \end{align*} $$
$$ \begin{align*} \left\|\varphi(t,a)^{1-\gamma_i} \left( \mathcal{H}_i(y_1,y_2)\right)(t)\right\| &\leq \| \xi_i\| + \frac{ \Vert h_i\Vert_{ L^{\frac{1}{\mu_i}}_{\varphi} } }{\Gamma(\alpha_i)} \left(\frac{1-\mu_i}{\alpha_i -\mu_i}\right)^{1-\mu_i}\varphi(t,a)^{1 + \alpha_i - \gamma_i -\mu_i } \\ &\quad + K \displaystyle\sum_{j=1}^{2}\frac{\varphi(t,a)^{1-\gamma_i} \Vert h_i\Vert_{ L^{\frac{1}{\mu_i}}_{\varphi} } }{\Gamma(\alpha_i)} \left( \Theta_{\frac{\alpha_i -\mu_i}{1-\mu_i}, \frac{1-\gamma_{j} }{1-\mu_i}} (a,t,t,\varphi) \right)^{1-\mu_i}\\ &\leq \widehat{K}_i,\quad i=1,2. \end{align*} $$
Thus,
Consequently,
This shows that
![]() $\mathcal {H}$
transforms
$\mathcal {H}$
transforms
![]() $\Omega _{K}$
into itself.
$\Omega _{K}$
into itself.
Step 2. The continuity of
![]() $\mathcal {H}(\cdot ,\cdot )$
.
$\mathcal {H}(\cdot ,\cdot )$
.
Let
![]() $\{y_{1,n},y_{2,n}\} \in \Omega _q$
such that
$\{y_{1,n},y_{2,n}\} \in \Omega _q$
such that
![]() $(y_{1,n},y_{2,n})\to (y_{1},y_{2})$
as
$(y_{1,n},y_{2,n})\to (y_{1},y_{2})$
as
![]() $ n \longrightarrow \infty $
. Making use of the Carathéodory condition of
$ n \longrightarrow \infty $
. Making use of the Carathéodory condition of
![]() $g_i$
,
$g_i$
,
![]() $i=1,2$
, we easily have
$i=1,2$
, we easily have
Next, by (H2), one gets
 $$ \begin{align*} &\hspace{-0.9cm} \left\|g_i(s, y_{1,n}(s), y_{2,n}(s)) - g_i(s,y_{1}(s), y_{2}(s))\right\|\\[0.2cm] &\leq \left\|g_i(s, y_{1,n}(s), y_{2,n}(s))\Vert + \Vert g_i(s,y_{1}(s), y_{2}(s))\right\|\\[0.1cm] &\leq 2 h_i(s) ( 1 + \Vert y_1(t)\Vert + \Vert y_2(t)\Vert ) \\ &\leq 2 h_i(s)\Big(1+ K \displaystyle\sum_{j=1}^{2} \varphi(s,a)^{\gamma_{j} -1}\Big). \end{align*} $$
$$ \begin{align*} &\hspace{-0.9cm} \left\|g_i(s, y_{1,n}(s), y_{2,n}(s)) - g_i(s,y_{1}(s), y_{2}(s))\right\|\\[0.2cm] &\leq \left\|g_i(s, y_{1,n}(s), y_{2,n}(s))\Vert + \Vert g_i(s,y_{1}(s), y_{2}(s))\right\|\\[0.1cm] &\leq 2 h_i(s) ( 1 + \Vert y_1(t)\Vert + \Vert y_2(t)\Vert ) \\ &\leq 2 h_i(s)\Big(1+ K \displaystyle\sum_{j=1}^{2} \varphi(s,a)^{\gamma_{j} -1}\Big). \end{align*} $$
Since, the function
 $s \mapsto h_i(s) \Big (1+ K \displaystyle\sum\limits _{j=1}^{2} \varphi (s,a)^{\gamma _{j} -1}\Big ) $
is Lebesgue integrable over
$s \mapsto h_i(s) \Big (1+ K \displaystyle\sum\limits _{j=1}^{2} \varphi (s,a)^{\gamma _{j} -1}\Big ) $
is Lebesgue integrable over
![]() $[a, t]$
, so is the function
$[a, t]$
, so is the function
 $s \mapsto h_i(s) \varphi (t,s)^{\alpha _i -1} \Big (1+ K \displaystyle \displaystyle\sum\limits _{j=1}^{2} \varphi (s,a)^{\gamma _{j} -1}\Big ) $
. Then it follows from the Lebesgue dominated convergence theorem that
$s \mapsto h_i(s) \varphi (t,s)^{\alpha _i -1} \Big (1+ K \displaystyle \displaystyle\sum\limits _{j=1}^{2} \varphi (s,a)^{\gamma _{j} -1}\Big ) $
. Then it follows from the Lebesgue dominated convergence theorem that
 $$ \begin{align*} &\hspace{-0.2cm} \left\| \varphi(t,a)^{1-\gamma_i}\left[ \mathcal{H}_i(y_{1,n}, y_{2,n})(t)- \mathcal{H}_i(y_{1}, y_{2})(t)\right]\right\| \\[0.3cm] &\hspace{-0.2cm}\leq \frac{\varphi(t,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi(t,s)^{\alpha_i -1} \varphi'(s) \left\|g_i(s, y_{1,n}(s), y_{2,n}(s)) - g_i(s,y_{1}(s), y_{2}(s))\right\|d s \to 0 \end{align*} $$
$$ \begin{align*} &\hspace{-0.2cm} \left\| \varphi(t,a)^{1-\gamma_i}\left[ \mathcal{H}_i(y_{1,n}, y_{2,n})(t)- \mathcal{H}_i(y_{1}, y_{2})(t)\right]\right\| \\[0.3cm] &\hspace{-0.2cm}\leq \frac{\varphi(t,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t} \varphi(t,s)^{\alpha_i -1} \varphi'(s) \left\|g_i(s, y_{1,n}(s), y_{2,n}(s)) - g_i(s,y_{1}(s), y_{2}(s))\right\|d s \to 0 \end{align*} $$
as
![]() $n \longrightarrow \infty $
for all
$n \longrightarrow \infty $
for all
![]() $t \in I$
, which leads to
$t \in I$
, which leads to
for any
![]() $t \in I$
. Therefore,
$t \in I$
. Therefore,
Accordingly, the operator
![]() $\mathcal {H}(\cdot ,\cdot )$
is continuous.
$\mathcal {H}(\cdot ,\cdot )$
is continuous.
Step 3.
![]() $\mathcal {H}(\Omega _{q})$
is equicontinuous.
$\mathcal {H}(\Omega _{q})$
is equicontinuous.
Let
![]() $(y_1,y_2)\in \Omega _{q}$
and
$(y_1,y_2)\in \Omega _{q}$
and
![]() $a<t_1<t_2\leq b$
. Then for
$a<t_1<t_2\leq b$
. Then for
![]() $i=1,2$
, we have
$i=1,2$
, we have
 $$ \begin{align*}\begin{array}{ll} &\hspace{-0.5cm} \left\| \varphi(t_2,a)^{1-\gamma_i} (\mathcal{H}_i(y_1,y_2))(t_2)-\varphi(t_1,a)^{1-\gamma_i}(\mathcal{H}_i(y_1,y_2))(t_1)\right\| \\[0.3cm] &\leq \displaystyle \Bigg\|\frac{\varphi(t_2,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t_{2}}\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} g_i(s, y_1(s) ,y_2(s)) d s \\[0.3cm] &\hspace{2cm} - \displaystyle\frac{\varphi(t_1,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t_{1}}\varphi'(s) \varphi(t_1,s)^{\alpha_i -1} g_i(s, y_1(s) ,y_2(s)) d s \Bigg\|\\[0.3cm] &\leq J_0 +J_1, \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ll} &\hspace{-0.5cm} \left\| \varphi(t_2,a)^{1-\gamma_i} (\mathcal{H}_i(y_1,y_2))(t_2)-\varphi(t_1,a)^{1-\gamma_i}(\mathcal{H}_i(y_1,y_2))(t_1)\right\| \\[0.3cm] &\leq \displaystyle \Bigg\|\frac{\varphi(t_2,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t_{2}}\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} g_i(s, y_1(s) ,y_2(s)) d s \\[0.3cm] &\hspace{2cm} - \displaystyle\frac{\varphi(t_1,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t_{1}}\varphi'(s) \varphi(t_1,s)^{\alpha_i -1} g_i(s, y_1(s) ,y_2(s)) d s \Bigg\|\\[0.3cm] &\leq J_0 +J_1, \end{array} \end{align*} $$
where
 $$ \begin{align*}J_0 = \frac{\varphi(t_2,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{t_1}^{t_{2}}\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} \|g_i(s, y_1(s) ,y_2(s))\| d s, \end{align*} $$
$$ \begin{align*}J_0 = \frac{\varphi(t_2,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{t_1}^{t_{2}}\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} \|g_i(s, y_1(s) ,y_2(s))\| d s, \end{align*} $$
and
 $$ \begin{align*}J_1 &= \Bigg\|\displaystyle \frac{\varphi(t_2,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t_{1}}\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} g_i(s, y_1(s) ,y_2(s)) d s \\ &\hspace{2cm} - \displaystyle\frac{\varphi(t_1,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t_{1}}\varphi'(s) \varphi(t_1,s)^{\alpha_i -1} g_i(s, y_1(s) ,y_2(s)) d s \Bigg\|. \end{align*} $$
$$ \begin{align*}J_1 &= \Bigg\|\displaystyle \frac{\varphi(t_2,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t_{1}}\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} g_i(s, y_1(s) ,y_2(s)) d s \\ &\hspace{2cm} - \displaystyle\frac{\varphi(t_1,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t_{1}}\varphi'(s) \varphi(t_1,s)^{\alpha_i -1} g_i(s, y_1(s) ,y_2(s)) d s \Bigg\|. \end{align*} $$
Next, applying the Hölder inequality, we conclude that
 $$ \begin{align*}J_0 &\leq \displaystyle\frac{\varphi(t_2,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{t_1}^{t_{2}}\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} h_i(s)( 1+ \Vert y_1(s) \Vert +\Vert y_2(s) \Vert ) d s\\[0.3cm] &\leq \displaystyle\frac{ \varphi(t_2,a)^{1-\gamma_i} \Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}} }{\Gamma(\alpha_i)} \left( \int_{t_1}^{t_{2}} \varphi(t_2,s)^{\frac{\alpha_i -1}{1-\mu_i}}d\varphi(s) \right)^{1-\mu_i}\\[0.4cm] & \quad + \displaystyle K \displaystyle\sum_{j=1}^{2}\frac{ \varphi(t_2,a)^{1-\gamma_i} \Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}} }{\Gamma(\alpha_i)} \left( \int_{t_1}^{t_{2}} \varphi(t_2,s)^{\frac{\alpha_i -1}{1-\mu_i}} \varphi(s,a)^{\frac{\gamma_{j} -1}{1-\mu_i}} d\varphi(s) \right)^{1-\mu_i}, \end{align*} $$
$$ \begin{align*}J_0 &\leq \displaystyle\frac{\varphi(t_2,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{t_1}^{t_{2}}\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} h_i(s)( 1+ \Vert y_1(s) \Vert +\Vert y_2(s) \Vert ) d s\\[0.3cm] &\leq \displaystyle\frac{ \varphi(t_2,a)^{1-\gamma_i} \Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}} }{\Gamma(\alpha_i)} \left( \int_{t_1}^{t_{2}} \varphi(t_2,s)^{\frac{\alpha_i -1}{1-\mu_i}}d\varphi(s) \right)^{1-\mu_i}\\[0.4cm] & \quad + \displaystyle K \displaystyle\sum_{j=1}^{2}\frac{ \varphi(t_2,a)^{1-\gamma_i} \Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}} }{\Gamma(\alpha_i)} \left( \int_{t_1}^{t_{2}} \varphi(t_2,s)^{\frac{\alpha_i -1}{1-\mu_i}} \varphi(s,a)^{\frac{\gamma_{j} -1}{1-\mu_i}} d\varphi(s) \right)^{1-\mu_i}, \end{align*} $$
and hence,
 $$ \begin{align*}\begin{array}{l} J_0 \leq \displaystyle \frac{ \varphi(t_2,a)^{1-\gamma_i} \Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi} } }{\Gamma(\alpha_i)} \Bigg[\frac{\varphi(t_2,t_1)^{\alpha_i -1} }{\theta_{i}^{1-\mu_i} } + K \displaystyle\sum_{j=1}^{2} \left( \Theta_{\theta_i, \vartheta_{i,j}} (t_1,t_2,t_2,\varphi) \right)^{1-\mu_i}\Bigg]. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{l} J_0 \leq \displaystyle \frac{ \varphi(t_2,a)^{1-\gamma_i} \Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi} } }{\Gamma(\alpha_i)} \Bigg[\frac{\varphi(t_2,t_1)^{\alpha_i -1} }{\theta_{i}^{1-\mu_i} } + K \displaystyle\sum_{j=1}^{2} \left( \Theta_{\theta_i, \vartheta_{i,j}} (t_1,t_2,t_2,\varphi) \right)^{1-\mu_i}\Bigg]. \end{array} \end{align*} $$
Now, using Remark 2.3, we obtain
and
where
 $$ \begin{align*}J_2 &= \displaystyle\frac{|\varphi(t_2,a)^{1-\gamma_i} - \varphi(t_1,a)^{1-\gamma_i}|}{\Gamma(\alpha_i)} \int_{a}^{t_{1}}\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} \Vert g_i(s, y_1(s) ,y_2(s))\Vert d s, \\[0.6cm] J_3 &= \displaystyle\frac{\varphi(t_1,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t_{1}}\varphi'(s)|\varphi(t_2,s)^{\alpha_i -1} - \varphi(t_1,s)^{\alpha_i -1}| \Vert g_i(s, y_1(s) ,y_2(s))\Vert d s. \end{align*} $$
$$ \begin{align*}J_2 &= \displaystyle\frac{|\varphi(t_2,a)^{1-\gamma_i} - \varphi(t_1,a)^{1-\gamma_i}|}{\Gamma(\alpha_i)} \int_{a}^{t_{1}}\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} \Vert g_i(s, y_1(s) ,y_2(s))\Vert d s, \\[0.6cm] J_3 &= \displaystyle\frac{\varphi(t_1,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \int_{a}^{t_{1}}\varphi'(s)|\varphi(t_2,s)^{\alpha_i -1} - \varphi(t_1,s)^{\alpha_i -1}| \Vert g_i(s, y_1(s) ,y_2(s))\Vert d s. \end{align*} $$
Then,
on the other hand,
![]() $\varphi (t_2,s)^{\alpha _i -1} \leq \varphi (t_1,s)^{\alpha _i -1}$
. Therefore
$\varphi (t_2,s)^{\alpha _i -1} \leq \varphi (t_1,s)^{\alpha _i -1}$
. Therefore
 $$ \begin{align*}J_3 &\leq \displaystyle \frac{\varphi(t_1,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \left( \int_{a}^{t_{1}}h_i(s)\varphi'(s)\varphi(t_1,s)^{\alpha_i -1} d s -\int_{a}^{t_{1}}h_i(s)\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} d s\right)\\[0.3cm] & \quad + \displaystyle \frac{\varphi(t_1,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} K \displaystyle\sum_{j=1}^{2} \int_{a}^{t_{1}}h_i(s)\varphi'(s)\Big(\varphi(t_1,s)^{\alpha_i -1} - \varphi(t_2,s)^{\alpha_i -1}\Big) \varphi(s,a)^{\gamma_{j} -1} ds. \end{align*} $$
$$ \begin{align*}J_3 &\leq \displaystyle \frac{\varphi(t_1,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} \left( \int_{a}^{t_{1}}h_i(s)\varphi'(s)\varphi(t_1,s)^{\alpha_i -1} d s -\int_{a}^{t_{1}}h_i(s)\varphi'(s) \varphi(t_2,s)^{\alpha_i -1} d s\right)\\[0.3cm] & \quad + \displaystyle \frac{\varphi(t_1,a)^{1-\gamma_i}}{\Gamma(\alpha_i)} K \displaystyle\sum_{j=1}^{2} \int_{a}^{t_{1}}h_i(s)\varphi'(s)\Big(\varphi(t_1,s)^{\alpha_i -1} - \varphi(t_2,s)^{\alpha_i -1}\Big) \varphi(s,a)^{\gamma_{j} -1} ds. \end{align*} $$
Then,
 $$ \begin{align*} J_3 &\leq \displaystyle \frac{\varphi(t_1,a)^{1-\gamma_i}\Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}}}{\Gamma(\alpha_i)} \left[\left( \Theta_{\theta_i, 0} (a,t_1,t_1,\varphi) \right)^{1-\mu_i} - \left( \Theta_{\theta_i, 0} (a,t_1,t_2,\varphi) \right)^{1-\mu_i} \right]\\[0.5cm] & \quad + \displaystyle \frac{\varphi(t_1,a)^{1-\gamma_i}\Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}}}{\Gamma(\alpha_i)} K \displaystyle\sum_{j=1}^{2} \Bigg[\left( \Theta_{\theta_i, \vartheta_{i,j}} (a,t_1,t_1,\varphi) \right)^{1-\mu_i} \\[0.5cm] & \qquad -\left( \Theta_{\theta_i, \vartheta_{i,j}} (a,t_1,t_2,\varphi) \right)^{1-\mu_i} \Bigg]. \end{align*} $$
$$ \begin{align*} J_3 &\leq \displaystyle \frac{\varphi(t_1,a)^{1-\gamma_i}\Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}}}{\Gamma(\alpha_i)} \left[\left( \Theta_{\theta_i, 0} (a,t_1,t_1,\varphi) \right)^{1-\mu_i} - \left( \Theta_{\theta_i, 0} (a,t_1,t_2,\varphi) \right)^{1-\mu_i} \right]\\[0.5cm] & \quad + \displaystyle \frac{\varphi(t_1,a)^{1-\gamma_i}\Vert h_i\Vert_{L^{\frac{1}{\mu_i}}_{\varphi}}}{\Gamma(\alpha_i)} K \displaystyle\sum_{j=1}^{2} \Bigg[\left( \Theta_{\theta_i, \vartheta_{i,j}} (a,t_1,t_1,\varphi) \right)^{1-\mu_i} \\[0.5cm] & \qquad -\left( \Theta_{\theta_i, \vartheta_{i,j}} (a,t_1,t_2,\varphi) \right)^{1-\mu_i} \Bigg]. \end{align*} $$
So,
Hence,
Thus, we conclude that
![]() $\mathcal {H}(\Omega _{q})$
is equicontinuous.
$\mathcal {H}(\Omega _{q})$
is equicontinuous.
Step 4. Condition (2.9) holds. For every bounded subset
![]() $\mathbb {J}^1\times \mathbb {J}^2\subset \mathcal {C}_{1-\gamma _1}^{\varphi }(I,\mathbb {E})\times \mathcal {C}_{1-\gamma _2}^{\varphi }(I,\mathbb {E})$
, we define the MNC as
$\mathbb {J}^1\times \mathbb {J}^2\subset \mathcal {C}_{1-\gamma _1}^{\varphi }(I,\mathbb {E})\times \mathcal {C}_{1-\gamma _2}^{\varphi }(I,\mathbb {E})$
, we define the MNC as
where
By using Lemma 2.10 and Example 2.15,
![]() $\widehat {\Lambda }_{\mathcal {C}_{1-\gamma _1}^{\varphi } \times \mathcal {C}_{1-\gamma _2}^{\varphi }}$
satisfies all properties of the Hausdorff MNC mentioned in Lemma 2.8.
$\widehat {\Lambda }_{\mathcal {C}_{1-\gamma _1}^{\varphi } \times \mathcal {C}_{1-\gamma _2}^{\varphi }}$
satisfies all properties of the Hausdorff MNC mentioned in Lemma 2.8.
Now, let
![]() $\mathscr {A} = (\mathbb {A}^1,\mathbb {A}^2)$
be a bounded set belongs to
$\mathscr {A} = (\mathbb {A}^1,\mathbb {A}^2)$
be a bounded set belongs to
![]() $ \overline {conv} \mathcal {H}(\Omega _{K})$
, using Lemma 2.12, it follows that for a given
$ \overline {conv} \mathcal {H}(\Omega _{K})$
, using Lemma 2.12, it follows that for a given
![]() $\epsilon _i> 0$
(
$\epsilon _i> 0$
(
![]() $i=1,2$
), there exists
$i=1,2$
), there exists
![]() $\{(y^{1,n} ,y^{2,n}) \}_{n=1}^{+\infty }\subseteq \mathscr {A}$
such that, for all
$\{(y^{1,n} ,y^{2,n}) \}_{n=1}^{+\infty }\subseteq \mathscr {A}$
such that, for all
![]() $t \in I$
,
$t \in I$
,
 $$ \begin{align} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_i}^{\varphi}}\Big(\mathcal{H}_i(\mathscr{A})(t) \Big) &= \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_i}^{\varphi}}\Big(\big\{(\mathcal{H}_i(y^{1},y^{2}))(t) ~:~ (y^{1},y^{2}) \in \mathscr{A} \big\} \Big) \\ & \leq 2 \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_i}^{\varphi}}\Big(\big\{(\mathcal{H}_i(y^{1,n},y^{2,n}))(t)\big\}_{n=1}^{+\infty} \Big) + \varepsilon_i,\quad i=1,2.\nonumber \end{align} $$
$$ \begin{align} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_i}^{\varphi}}\Big(\mathcal{H}_i(\mathscr{A})(t) \Big) &= \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_i}^{\varphi}}\Big(\big\{(\mathcal{H}_i(y^{1},y^{2}))(t) ~:~ (y^{1},y^{2}) \in \mathscr{A} \big\} \Big) \\ & \leq 2 \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_i}^{\varphi}}\Big(\big\{(\mathcal{H}_i(y^{1,n},y^{2,n}))(t)\big\}_{n=1}^{+\infty} \Big) + \varepsilon_i,\quad i=1,2.\nonumber \end{align} $$
From
wet get
Now, we estimate the quantity
![]() $\widehat {\Lambda }_{\mathcal {C}_{1-\gamma _i}^{\varphi }}\Big (\big \{(\mathcal {H}_i(y^{1,n},y^{2,n}))(\cdot )\big \}_{n=1}^{+\infty } \Big )$
. Using (H3), for all
$\widehat {\Lambda }_{\mathcal {C}_{1-\gamma _i}^{\varphi }}\Big (\big \{(\mathcal {H}_i(y^{1,n},y^{2,n}))(\cdot )\big \}_{n=1}^{+\infty } \Big )$
. Using (H3), for all
![]() $s \in [a,t]$
, one has for
$s \in [a,t]$
, one has for
![]() $i=1,2$
$i=1,2$
 $$ \begin{align*}\begin{array}{ll} &\hspace{-0.5cm} \displaystyle\Lambda\left(\Big\{ \varphi'(s) \varphi(t,s)^{\alpha_i-1}g_{i}(s,y^{1,n}(s),y^{2,n}(s))\Big\} _{n=1}^{+\infty}\right)\\[0.1cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \varphi'(s) \varphi(t,s)^{\alpha_i-1} \eta_{i,j}(s) \Lambda(\{y^{j,n}(s)\}_{n=1}^{+\infty}) \\[0.3cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \eta_{i,j}(s) \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} \Lambda(\{y_{\gamma_j}^{j,n}(s)\}_{n=1}^{+\infty})\\[0.3cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \eta_{i,j}(s) \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{\aleph s} \sup_{a\leq s\leq t} e^{-\aleph s} \Lambda(\{y_{\gamma_j}^{j,n}(s)\}_{n=1}^{+\infty}) \\[0.5cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \eta_{i,j}(s) \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{\aleph s} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_j}^{\varphi}}(\{y^{j,n}\}_{n=1}^{+\infty}). \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ll} &\hspace{-0.5cm} \displaystyle\Lambda\left(\Big\{ \varphi'(s) \varphi(t,s)^{\alpha_i-1}g_{i}(s,y^{1,n}(s),y^{2,n}(s))\Big\} _{n=1}^{+\infty}\right)\\[0.1cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \varphi'(s) \varphi(t,s)^{\alpha_i-1} \eta_{i,j}(s) \Lambda(\{y^{j,n}(s)\}_{n=1}^{+\infty}) \\[0.3cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \eta_{i,j}(s) \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} \Lambda(\{y_{\gamma_j}^{j,n}(s)\}_{n=1}^{+\infty})\\[0.3cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \eta_{i,j}(s) \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{\aleph s} \sup_{a\leq s\leq t} e^{-\aleph s} \Lambda(\{y_{\gamma_j}^{j,n}(s)\}_{n=1}^{+\infty}) \\[0.5cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \eta_{i,j}(s) \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{\aleph s} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_j}^{\varphi}}(\{y^{j,n}\}_{n=1}^{+\infty}). \end{array} \end{align*} $$
Thus, Lemma 2.11 entails that, for all
![]() $t \in I$
and
$t \in I$
and
![]() $s \leq t$
,
$s \leq t$
,
 $$ \begin{align*}\begin{array}{ll} &\hspace{-0.3cm} \displaystyle\Lambda \Big(\big\{ \mathcal{I}_{a^+}^{\alpha_i,\varphi}g_{i}(t,y^{1,n}(t),y^{2,n}(t))\big\}_{n=1}^{+\infty} \Big) \\[0.3cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \frac{2 \Vert \eta_{i,j} \Vert_{L^{\infty}}}{\Gamma(\alpha_i)} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_j}^{\varphi}}(\{y^{j,n}\}_{n=1}^{+\infty}) \int_{a}^{t} \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{\aleph s} ds. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ll} &\hspace{-0.3cm} \displaystyle\Lambda \Big(\big\{ \mathcal{I}_{a^+}^{\alpha_i,\varphi}g_{i}(t,y^{1,n}(t),y^{2,n}(t))\big\}_{n=1}^{+\infty} \Big) \\[0.3cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \frac{2 \Vert \eta_{i,j} \Vert_{L^{\infty}}}{\Gamma(\alpha_i)} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_j}^{\varphi}}(\{y^{j,n}\}_{n=1}^{+\infty}) \int_{a}^{t} \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{\aleph s} ds. \end{array} \end{align*} $$
Hence,
 $$ \begin{align*}\begin{array}{ll} &\hspace{-0.2cm} \displaystyle\Lambda\left( \left\lbrace \varphi(t,a)^{1- \gamma_i } \mathcal{H}_i(y^{1,n}(t),y^{2,n}(t))\right\rbrace _{n=1}^{+\infty}\right) \\[0.3cm] &\hspace{-0.2cm}\leq \displaystyle \displaystyle\sum_{j=1}^{2} \frac{2 \Vert \eta_{i,j} \Vert_{L^{\infty}}}{\Gamma(\alpha_i)} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_j}^{\varphi}}(\{y^{j,n}\}_{n=1}^{+\infty}) \varphi(b,a)^{1- \gamma_i } \int_{a}^{t} \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{\aleph s} ds. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ll} &\hspace{-0.2cm} \displaystyle\Lambda\left( \left\lbrace \varphi(t,a)^{1- \gamma_i } \mathcal{H}_i(y^{1,n}(t),y^{2,n}(t))\right\rbrace _{n=1}^{+\infty}\right) \\[0.3cm] &\hspace{-0.2cm}\leq \displaystyle \displaystyle\sum_{j=1}^{2} \frac{2 \Vert \eta_{i,j} \Vert_{L^{\infty}}}{\Gamma(\alpha_i)} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_j}^{\varphi}}(\{y^{j,n}\}_{n=1}^{+\infty}) \varphi(b,a)^{1- \gamma_i } \int_{a}^{t} \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{\aleph s} ds. \end{array} \end{align*} $$
Multiplying both sides by
![]() $e^{-\aleph t}$
, we obtain
$e^{-\aleph t}$
, we obtain
 $$ \begin{align*}\begin{array}{ll} & \hspace{-0.3cm} \displaystyle \sup_{t \in J} e^{-\aleph t}\Lambda\left( \left\lbrace \varphi(t,a)^{1- \gamma_i } \mathcal{H}_i(y^{1,n}(t),y^{2,n}(t))\right\rbrace _{n=1}^{+\infty}\right) \\[0.3cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \frac{2 \Vert \eta_{i,j} \Vert_{L^{\infty}}}{\Gamma(\alpha_i)} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_j}^{\varphi}}(\{y^{j,n}\}_{n=1}^{+\infty}) \varphi(b,a)^{1- \gamma_i } \times\\[0.3cm] &\qquad \displaystyle \sup_{t \in I} \int_{a}^{t} \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{-\aleph(t-s)} ds. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{ll} & \hspace{-0.3cm} \displaystyle \sup_{t \in J} e^{-\aleph t}\Lambda\left( \left\lbrace \varphi(t,a)^{1- \gamma_i } \mathcal{H}_i(y^{1,n}(t),y^{2,n}(t))\right\rbrace _{n=1}^{+\infty}\right) \\[0.3cm] &\leq \displaystyle \displaystyle\sum_{j=1}^{2} \frac{2 \Vert \eta_{i,j} \Vert_{L^{\infty}}}{\Gamma(\alpha_i)} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_j}^{\varphi}}(\{y^{j,n}\}_{n=1}^{+\infty}) \varphi(b,a)^{1- \gamma_i } \times\\[0.3cm] &\qquad \displaystyle \sup_{t \in I} \int_{a}^{t} \varphi'(s) \varphi(t,s)^{\alpha_i-1} \varphi(s,a)^{\gamma_j-1} e^{-\aleph(t-s)} ds. \end{array} \end{align*} $$
So,
 $$ \begin{align*}\widehat{\Lambda}_{\mathcal{C}_{1-\gamma_i}^{\varphi}}\Big(\big\{\mathcal{H}_i(y^{1,n},y^{2,n})\big\}_{n=1}^{+\infty} \Big) \leq \displaystyle\sum_{j=1}^{2} \mathcal{L}_{i,j}(\aleph) \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_j}^{\varphi}}(\{y^{j,n}\}_{n=1}^{+\infty}), \end{align*} $$
$$ \begin{align*}\widehat{\Lambda}_{\mathcal{C}_{1-\gamma_i}^{\varphi}}\Big(\big\{\mathcal{H}_i(y^{1,n},y^{2,n})\big\}_{n=1}^{+\infty} \Big) \leq \displaystyle\sum_{j=1}^{2} \mathcal{L}_{i,j}(\aleph) \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_j}^{\varphi}}(\{y^{j,n}\}_{n=1}^{+\infty}), \end{align*} $$
where
![]() $\mathcal {L}_{i,j}(\aleph ), i=1,2, j=1,2$
are defined in (2.1). Hence,
$\mathcal {L}_{i,j}(\aleph ), i=1,2, j=1,2$
are defined in (2.1). Hence,
 $$ \begin{align*} &\hspace{-0.7cm} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_i}^{\varphi}}\Big(\big\{\mathcal{H}_i(y^{1,n},y^{2,n})\big\}_{n=1}^{+\infty} \Big)\\ &\leq \max_{1\leq j\leq 2}\{\mathcal{L}_{i,j}(\aleph)\} \Big( \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi}}(\{y^{1,n}\}_{n=1}^{+\infty}) + \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_2}^{\varphi}}(\{y^{2,n}\}_{n=1}^{+\infty})\Big)\\ &= \max_{1\leq j\leq 2}\{\mathcal{L}_{i,j}(\aleph)\} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi} \times \mathcal{C}_{1-\gamma_2}^{\varphi}}(\{(y^{1,n},y^{2,n})\}_{n=1}^{+\infty}). \end{align*} $$
$$ \begin{align*} &\hspace{-0.7cm} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_i}^{\varphi}}\Big(\big\{\mathcal{H}_i(y^{1,n},y^{2,n})\big\}_{n=1}^{+\infty} \Big)\\ &\leq \max_{1\leq j\leq 2}\{\mathcal{L}_{i,j}(\aleph)\} \Big( \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi}}(\{y^{1,n}\}_{n=1}^{+\infty}) + \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_2}^{\varphi}}(\{y^{2,n}\}_{n=1}^{+\infty})\Big)\\ &= \max_{1\leq j\leq 2}\{\mathcal{L}_{i,j}(\aleph)\} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi} \times \mathcal{C}_{1-\gamma_2}^{\varphi}}(\{(y^{1,n},y^{2,n})\}_{n=1}^{+\infty}). \end{align*} $$
The last inequality together with the fact that
yields
From (3.6) and (3.9), one gets
Then,
 $$ \begin{align*}&\hspace{-0.7cm} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi} \times \mathcal{C}_{1-\gamma_2}^{\varphi}}\Big(\mathcal{H}(\mathscr{A}) \Big)\\ &= \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi}}\Big(\mathcal{H}_i(\mathscr{A}) \Big) + \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_2}^{\varphi}}\Big(\mathcal{H}_i(\mathscr{A})\Big) \\ &\leq 2 \Big( \max_{1\leq j\leq 2}\{\mathcal{L}_{1,j}(\aleph)\} + \max_{1\leq j\leq 2}\{\mathcal{L}_{2,j}(\aleph)\} \Big) \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi} \times \mathcal{C}_{1-\gamma_2}^{\varphi}}(\mathscr{A}) + \varepsilon_3 \\ &\leq 4 \max_{1\leq i\leq 2} \{ \max_{1\leq j\leq 2}\{\mathcal{L}_{i,j}(\aleph)\} \} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi} \times \mathcal{C}_{1-\gamma_2}^{\varphi}}(\mathscr{A}) + \varepsilon_3, \end{align*} $$
$$ \begin{align*}&\hspace{-0.7cm} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi} \times \mathcal{C}_{1-\gamma_2}^{\varphi}}\Big(\mathcal{H}(\mathscr{A}) \Big)\\ &= \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi}}\Big(\mathcal{H}_i(\mathscr{A}) \Big) + \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_2}^{\varphi}}\Big(\mathcal{H}_i(\mathscr{A})\Big) \\ &\leq 2 \Big( \max_{1\leq j\leq 2}\{\mathcal{L}_{1,j}(\aleph)\} + \max_{1\leq j\leq 2}\{\mathcal{L}_{2,j}(\aleph)\} \Big) \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi} \times \mathcal{C}_{1-\gamma_2}^{\varphi}}(\mathscr{A}) + \varepsilon_3 \\ &\leq 4 \max_{1\leq i\leq 2} \{ \max_{1\leq j\leq 2}\{\mathcal{L}_{i,j}(\aleph)\} \} \widehat{\Lambda}_{\mathcal{C}_{1-\gamma_1}^{\varphi} \times \mathcal{C}_{1-\gamma_2}^{\varphi}}(\mathscr{A}) + \varepsilon_3, \end{align*} $$
where
![]() $\varepsilon _3 = \varepsilon _1 +\varepsilon _2 $
. Since
$\varepsilon _3 = \varepsilon _1 +\varepsilon _2 $
. Since
![]() $\varepsilon _3> 0$
is arbitrary, we have
$\varepsilon _3> 0$
is arbitrary, we have
From Remark 2.4, we deduce
![]() $4 \max _{1\leq i\leq 2} \{ \max _{1\leq j\leq 2}\{\mathcal {L}_{i,j}(\aleph )\} \} <1 $
.
$4 \max _{1\leq i\leq 2} \{ \max _{1\leq j\leq 2}\{\mathcal {L}_{i,j}(\aleph )\} \} <1 $
.
In view of Steps 1 to 4, we can apply Theorem 2.13 and deduce that
![]() $\mathcal {H}$
admits in
$\mathcal {H}$
admits in
![]() $\Omega _{K}$
, at least one fixed point which is a solution of system (1.1).
$\Omega _{K}$
, at least one fixed point which is a solution of system (1.1).
4 An example
Consider the Banach space
equipped with the norm
![]() $ \Vert z \Vert _{\mathbb {E}} = \sup\limits _{n \geq 1} |z^n|$
.
$ \Vert z \Vert _{\mathbb {E}} = \sup\limits _{n \geq 1} |z^n|$
.
We recall that the Hausdorff MNC
![]() $\Lambda $
in
$\Lambda $
in
![]() $\left (\mathbb {E}, \Vert \cdot \Vert _{\mathbb {E}} \right ) $
is defined as follows:
$\left (\mathbb {E}, \Vert \cdot \Vert _{\mathbb {E}} \right ) $
is defined as follows:
where
![]() $\mathbb {A}$
is a bounded subset in
$\mathbb {A}$
is a bounded subset in
![]() $\mathbb {E}$
and
$\mathbb {E}$
and
![]() $\mathrm {P}_n$
is the projection onto the linear span of the first n vectors in the standard basis (see [Reference Akhmerov, Kamenskii, Potapov, Rodkina and Sadovskii5, Reference Mursaleen25]).
$\mathrm {P}_n$
is the projection onto the linear span of the first n vectors in the standard basis (see [Reference Akhmerov, Kamenskii, Potapov, Rodkina and Sadovskii5, Reference Mursaleen25]).
Consider the following coupled system:
 $$ \begin{align} \left\{ \begin{array}{l} { }^{H} \mathcal{D}_{a^+}^{\alpha_1, \beta_1; t} y_1(t)= g_1(t,y_1(t),y_2(t)), \quad t\in I' := (0, b],~~ 0< b< \frac{1}{4e},\\[0.3cm] { }^{H} \mathcal{D}_{a^+}^{\alpha_2, \beta_2; t} y_2(t)= g_2(t,y_1(t),y_2(t)), \hspace{7pt} t \in I' := (0, b],~~ 0< b< \frac{1}{4e}, \\[0.3cm] \left(t^{1-\gamma_1} y_1\right)(0^+) = (0, 0,\dots, 0, \dots),\\[0.3cm] \left(t^{1-\gamma_2} y_2\right)(0^+) = (0, 0,\dots, 0, \dots). \\ \end{array} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{array}{l} { }^{H} \mathcal{D}_{a^+}^{\alpha_1, \beta_1; t} y_1(t)= g_1(t,y_1(t),y_2(t)), \quad t\in I' := (0, b],~~ 0< b< \frac{1}{4e},\\[0.3cm] { }^{H} \mathcal{D}_{a^+}^{\alpha_2, \beta_2; t} y_2(t)= g_2(t,y_1(t),y_2(t)), \hspace{7pt} t \in I' := (0, b],~~ 0< b< \frac{1}{4e}, \\[0.3cm] \left(t^{1-\gamma_1} y_1\right)(0^+) = (0, 0,\dots, 0, \dots),\\[0.3cm] \left(t^{1-\gamma_2} y_2\right)(0^+) = (0, 0,\dots, 0, \dots). \\ \end{array} \right. \end{align} $$
Note that (4.1) is a particular case of (1.1), where:
 $$ \begin{align*}a=0, ~~ \varphi(t)=L^{-1/\phi_{\min}} b^{\zeta} t, ~~ L= \max_{\substack{ 1\leq i\leq 2 \\ 1\leq j\leq 2 }} L_{i,j} , ~~ \phi_{i,j} = \theta_{i} +\vartheta_{i,i}-\vartheta_{i,j}, ~~ \mu_{\min} = \min_{1\leq i \leq 2}\mu_i \end{align*} $$
$$ \begin{align*}a=0, ~~ \varphi(t)=L^{-1/\phi_{\min}} b^{\zeta} t, ~~ L= \max_{\substack{ 1\leq i\leq 2 \\ 1\leq j\leq 2 }} L_{i,j} , ~~ \phi_{i,j} = \theta_{i} +\vartheta_{i,i}-\vartheta_{i,j}, ~~ \mu_{\min} = \min_{1\leq i \leq 2}\mu_i \end{align*} $$
 $$ \begin{align*}\zeta =\frac{1}{\phi_{\min}(1- \mu_{\min})} - 1, ~~ L_{i,j} = \Bigg\{ \frac{2^{\vartheta_{i,j}}}{\theta_i} + \frac{2^{1-\theta_i}}{1-\vartheta_{i,j}} \Bigg\},~~ \phi_{\min}=\min_{\substack{ 1\leq i\leq 2 \\ 1\leq j\leq 2 }} \phi_{i,j},~~ \end{align*} $$
$$ \begin{align*}\zeta =\frac{1}{\phi_{\min}(1- \mu_{\min})} - 1, ~~ L_{i,j} = \Bigg\{ \frac{2^{\vartheta_{i,j}}}{\theta_i} + \frac{2^{1-\theta_i}}{1-\vartheta_{i,j}} \Bigg\},~~ \phi_{\min}=\min_{\substack{ 1\leq i\leq 2 \\ 1\leq j\leq 2 }} \phi_{i,j},~~ \end{align*} $$
and for
![]() $t\in I$
,
$t\in I$
,
![]() $y_i =\{y^{i,n}\} _n \in \mathbb {E}$
,
$y_i =\{y^{i,n}\} _n \in \mathbb {E}$
,
One can easily deduce that the functions
![]() $g_i$
, (
$g_i$
, (
![]() $i=1,2$
) satisfy the Carathéodory type hypotheses, so (H1) holds.
$i=1,2$
) satisfy the Carathéodory type hypotheses, so (H1) holds.
To justify hypothesis (H2), let
![]() $t \in I$
and
$t \in I$
and
![]() $y_i =\{y^{i,n}\} _n \in \mathbb {E} $
,
$y_i =\{y^{i,n}\} _n \in \mathbb {E} $
,
![]() $(i=1,2)$
. We have
$(i=1,2)$
. We have
 $$ \begin{align*} \Vert g_1(t,y_1,y_2) \Vert_{\mathbb{E}} & = e^t \Big\Vert {\left\lbrace \arctan(|y^{1,n}| + |y^{2,n}|) + \frac{1}{n^2} \right\rbrace}_{n=1}^{\infty} \Big\Vert_{\mathbb{E}} \\ &\leq e^t \left( \sup_{n \geq 1}|y^{1,n}|+ \sup_{n \geq 1}|y^{2,n}| +1 \right) \\ &\leq e^t \left( \Vert y_{1}\Vert_{\mathbb{E}}+ \Vert y_{2}\Vert_{\mathbb{E}} +1 \right), \end{align*} $$
$$ \begin{align*} \Vert g_1(t,y_1,y_2) \Vert_{\mathbb{E}} & = e^t \Big\Vert {\left\lbrace \arctan(|y^{1,n}| + |y^{2,n}|) + \frac{1}{n^2} \right\rbrace}_{n=1}^{\infty} \Big\Vert_{\mathbb{E}} \\ &\leq e^t \left( \sup_{n \geq 1}|y^{1,n}|+ \sup_{n \geq 1}|y^{2,n}| +1 \right) \\ &\leq e^t \left( \Vert y_{1}\Vert_{\mathbb{E}}+ \Vert y_{2}\Vert_{\mathbb{E}} +1 \right), \end{align*} $$
and
 $$ \begin{align*} \Vert g_2(t,y_1,y_2)\Vert_{\mathbb{E}} & = e^{t}\Big\Vert {\left\lbrace \ln(|1+y^{1,n}|) +|y^{2,n}| + \frac{1}{n^2} \right\rbrace}_{n=1}^{\infty} \Big\Vert_{\mathbb{E}} \\ &\leq e^{t} \left( \sup_{n \geq 1}|y^{1,n}|+ \sup_{n \geq 1}|y^{2,n}| +1 \right) \\ &\leq e^{t}\left( \Vert y_{1}\Vert_{\mathbb{E}}+ \Vert y_{2}\Vert_{\mathbb{E}} +1 \right). \end{align*} $$
$$ \begin{align*} \Vert g_2(t,y_1,y_2)\Vert_{\mathbb{E}} & = e^{t}\Big\Vert {\left\lbrace \ln(|1+y^{1,n}|) +|y^{2,n}| + \frac{1}{n^2} \right\rbrace}_{n=1}^{\infty} \Big\Vert_{\mathbb{E}} \\ &\leq e^{t} \left( \sup_{n \geq 1}|y^{1,n}|+ \sup_{n \geq 1}|y^{2,n}| +1 \right) \\ &\leq e^{t}\left( \Vert y_{1}\Vert_{\mathbb{E}}+ \Vert y_{2}\Vert_{\mathbb{E}} +1 \right). \end{align*} $$
This shows that hypothesis (H2) holds, with
To prove (3.1), let
![]() $t \in I$
and
$t \in I$
and
![]() $z_i =\{z^{i,n}\} _n \in \mathbb {A}^{i}\subseteq \mathbb {E} $
,
$z_i =\{z^{i,n}\} _n \in \mathbb {A}^{i}\subseteq \mathbb {E} $
,
![]() $i=1,2$
. Fix
$i=1,2$
. Fix
![]() $n \in \mathbb {N}$
; then we have
$n \in \mathbb {N}$
; then we have
for all
![]() $k>n$
, which implies, by taking the supremum, that
$k>n$
, which implies, by taking the supremum, that
 $$ \begin{align*}&\hspace{-1cm} \sup_{(z_1,z_2) \in \mathbb{A}^{1}\times\mathbb{A}^{2}} \Vert \left( \mathrm{I} - \mathrm{P}_n \right) (\arctan(|y^{1,k}| +|y^{2,k}|))_k \Vert_{\infty}\\ &\leq \sup_{z_1 \in \mathbb{A}^{1}}\Vert \left( \mathrm{I} - \mathrm{P}_n \right)(z^{1,k})_k \Vert_{\infty} + \sup_{z_2 \in \mathbb{A}^{2}}\Vert \left( \mathrm{I} - \mathrm{P}_n \right)(z^{2,k})_k \Vert_{\infty}. \end{align*} $$
$$ \begin{align*}&\hspace{-1cm} \sup_{(z_1,z_2) \in \mathbb{A}^{1}\times\mathbb{A}^{2}} \Vert \left( \mathrm{I} - \mathrm{P}_n \right) (\arctan(|y^{1,k}| +|y^{2,k}|))_k \Vert_{\infty}\\ &\leq \sup_{z_1 \in \mathbb{A}^{1}}\Vert \left( \mathrm{I} - \mathrm{P}_n \right)(z^{1,k})_k \Vert_{\infty} + \sup_{z_2 \in \mathbb{A}^{2}}\Vert \left( \mathrm{I} - \mathrm{P}_n \right)(z^{2,k})_k \Vert_{\infty}. \end{align*} $$
Then
 $$ \begin{align*}&\hspace{-0.1cm} \lim_{n \to \infty}\sup_{(z_1,z_2) \in \mathbb{A}^{1}\times\mathbb{A}^{2}} \Vert \left( \mathrm{I} - \mathrm{P}_n \right) (\arctan(|y^{1,k}|+|y^{2,k}|))_k \Vert_{\infty}\\ &\leq \lim_{n \to \infty}\sup_{z_1 \in \mathbb{A}^{1}}\Vert \left( \mathrm{I} - \mathrm{P}_n \right) (z^{1,k})_k \Vert_{\infty} + \lim_{n \to \infty}\sup_{z_2 \in \mathbb{A}^{2}} \Vert \left( \mathrm{I} - \mathrm{P}_n \right) (z^{2,k})_k \Vert_{\infty}, \end{align*} $$
$$ \begin{align*}&\hspace{-0.1cm} \lim_{n \to \infty}\sup_{(z_1,z_2) \in \mathbb{A}^{1}\times\mathbb{A}^{2}} \Vert \left( \mathrm{I} - \mathrm{P}_n \right) (\arctan(|y^{1,k}|+|y^{2,k}|))_k \Vert_{\infty}\\ &\leq \lim_{n \to \infty}\sup_{z_1 \in \mathbb{A}^{1}}\Vert \left( \mathrm{I} - \mathrm{P}_n \right) (z^{1,k})_k \Vert_{\infty} + \lim_{n \to \infty}\sup_{z_2 \in \mathbb{A}^{2}} \Vert \left( \mathrm{I} - \mathrm{P}_n \right) (z^{2,k})_k \Vert_{\infty}, \end{align*} $$
which yields
 $$ \begin{align*} &\hspace{-0.1cm} \Lambda (g_1(t,\mathbb{A}^1,\mathbb{A}^2))\\ &= e^{t} \lim_{n \to \infty}\sup_{(z_1,z_2) \in \mathbb{A}^{1}\times\mathbb{A}^{2}} \left\Vert \left( \mathrm{I} - \mathrm{P}_n \right) \left(\arctan(|z^{1,k}| +|z^{2,k}| )+\frac{1}{k^2}\right)_k \right\Vert{}_{\infty}\\ &\leq e^{t} \Big[ \lim_{n \to \infty}\sup_{z_1 \in \mathbb{A}^{1}}\Vert \left( \mathrm{I} - \mathrm{P}_n \right) (z^{1,k} )_k \Vert_{\infty}\\ &\quad + \lim_{n \to \infty}\sup_{z_2 \in \mathbb{A}^{2}} \Vert \left( \mathrm{I} - \mathrm{P}_n \right) (z^{2,k})_k \Vert_{\infty} \Big]\\ &\leq \eta_{1,1}(t) \Lambda(\mathbb{A}^1) +\eta_{1,2}(t)\Lambda(\mathbb{A}^2), \end{align*} $$
$$ \begin{align*} &\hspace{-0.1cm} \Lambda (g_1(t,\mathbb{A}^1,\mathbb{A}^2))\\ &= e^{t} \lim_{n \to \infty}\sup_{(z_1,z_2) \in \mathbb{A}^{1}\times\mathbb{A}^{2}} \left\Vert \left( \mathrm{I} - \mathrm{P}_n \right) \left(\arctan(|z^{1,k}| +|z^{2,k}| )+\frac{1}{k^2}\right)_k \right\Vert{}_{\infty}\\ &\leq e^{t} \Big[ \lim_{n \to \infty}\sup_{z_1 \in \mathbb{A}^{1}}\Vert \left( \mathrm{I} - \mathrm{P}_n \right) (z^{1,k} )_k \Vert_{\infty}\\ &\quad + \lim_{n \to \infty}\sup_{z_2 \in \mathbb{A}^{2}} \Vert \left( \mathrm{I} - \mathrm{P}_n \right) (z^{2,k})_k \Vert_{\infty} \Big]\\ &\leq \eta_{1,1}(t) \Lambda(\mathbb{A}^1) +\eta_{1,2}(t)\Lambda(\mathbb{A}^2), \end{align*} $$
where
Similarly, one can obtain
where
Hence condition (H3) is verified. Now, it remains to show that (3.2) holds. To do this, from
![]() $\Gamma (\alpha _i)>1 $
for
$\Gamma (\alpha _i)>1 $
for
![]() $ 0<\alpha _i <1$
, we have
$ 0<\alpha _i <1$
, we have
 $$ \begin{align*}\widehat{K}_i \leq \Vert h\Vert_{L^{\frac{1}{\mu_i}}}\frac{\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i }}{ \theta_{i}^{1-\mu_i}} + K \displaystyle\sum_{j=1}^{2} \Vert h\Vert_{L^{\frac{1}{\mu_i}}} \left( \Theta_{\theta_i, \vartheta_{i,j}} (0,b,b,\varphi) \varphi(b,0)^{\vartheta_{i,i}} \right)^{1-\mu_i}. \end{align*} $$
$$ \begin{align*}\widehat{K}_i \leq \Vert h\Vert_{L^{\frac{1}{\mu_i}}}\frac{\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i }}{ \theta_{i}^{1-\mu_i}} + K \displaystyle\sum_{j=1}^{2} \Vert h\Vert_{L^{\frac{1}{\mu_i}}} \left( \Theta_{\theta_i, \vartheta_{i,j}} (0,b,b,\varphi) \varphi(b,0)^{\vartheta_{i,i}} \right)^{1-\mu_i}. \end{align*} $$
Then, by Lemma 2.2 and
![]() $ 0<\varphi (b,0) <1$
, we get
$ 0<\varphi (b,0) <1$
, we get
 $$ \begin{align*}\widehat{K}_i &\leq \displaystyle \Vert h\Vert_{L^{\frac{1}{\mu_i}}}\frac{\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i }}{ \theta_{i}^{1-\mu_i}} \\ &\qquad + K \displaystyle\sum_{j=1}^{2} \Vert h\Vert_{L^{\frac{1}{\mu_i}}} \left( \left(\frac{2^{\vartheta_{i,j}}}{\theta_i} +\frac{2^{1-\theta_i}}{1-\vartheta_{i,j}} \right) \varphi(b,0)^{\theta_i -\vartheta_{i,j}} \varphi(b,0)^{\vartheta_{i,i}} \right)^{1-\mu_i} \\ &\leq \displaystyle \Vert h\Vert_{L^{\frac{1}{\mu_i}}}\frac{\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i }}{ \theta_{i}^{1-\mu_i}} + 2 K \Vert h\Vert_{L^{\frac{1}{\mu_i}}} \left( L \left( L^{-1/\phi_{\min}} b^{\zeta +1} \right)^{\phi_{\min}} \right)^{1-\mu_i} \\ &\leq \displaystyle \Vert h\Vert_{L^{\frac{1}{\mu_i}}}\frac{\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i }}{ \theta_{i}^{1-\mu_i}} + 2 K \Vert h\Vert_{L^{\frac{1}{\mu_i}}} \left( b^{ \frac{1}{1-\mu_{\min}}} \right)^{1-\mu_{\min}} \\ &\leq \displaystyle \frac{\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i }}{\theta_{i}^{1-\mu_i}} \Vert h\Vert_{L^{\frac{1}{\mu_i}}} + 2 K b \Vert h\Vert_{L^{\frac{1}{\mu_i}}} \end{align*} $$
$$ \begin{align*}\widehat{K}_i &\leq \displaystyle \Vert h\Vert_{L^{\frac{1}{\mu_i}}}\frac{\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i }}{ \theta_{i}^{1-\mu_i}} \\ &\qquad + K \displaystyle\sum_{j=1}^{2} \Vert h\Vert_{L^{\frac{1}{\mu_i}}} \left( \left(\frac{2^{\vartheta_{i,j}}}{\theta_i} +\frac{2^{1-\theta_i}}{1-\vartheta_{i,j}} \right) \varphi(b,0)^{\theta_i -\vartheta_{i,j}} \varphi(b,0)^{\vartheta_{i,i}} \right)^{1-\mu_i} \\ &\leq \displaystyle \Vert h\Vert_{L^{\frac{1}{\mu_i}}}\frac{\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i }}{ \theta_{i}^{1-\mu_i}} + 2 K \Vert h\Vert_{L^{\frac{1}{\mu_i}}} \left( L \left( L^{-1/\phi_{\min}} b^{\zeta +1} \right)^{\phi_{\min}} \right)^{1-\mu_i} \\ &\leq \displaystyle \Vert h\Vert_{L^{\frac{1}{\mu_i}}}\frac{\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i }}{ \theta_{i}^{1-\mu_i}} + 2 K \Vert h\Vert_{L^{\frac{1}{\mu_i}}} \left( b^{ \frac{1}{1-\mu_{\min}}} \right)^{1-\mu_{\min}} \\ &\leq \displaystyle \frac{\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i }}{\theta_{i}^{1-\mu_i}} \Vert h\Vert_{L^{\frac{1}{\mu_i}}} + 2 K b \Vert h\Vert_{L^{\frac{1}{\mu_i}}} \end{align*} $$
and
Now, choose
 $$ \begin{align*} K &\geq \frac{2e\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i } }{\theta_{i}^{1-\mu_i}(1- 4be )} ,\quad i=1,2. \end{align*} $$
$$ \begin{align*} K &\geq \frac{2e\varphi(b,0)^{1 + \alpha_i - \gamma_i -\mu_i } }{\theta_{i}^{1-\mu_i}(1- 4be )} ,\quad i=1,2. \end{align*} $$
Hence,
Since, all hypotheses in Theorem 3.1 are verified, system (4.1) has at least one solution.