Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gruber, Peter M.
1979.
Contributions to Geometry.
p.
186.
Tóth, G. Fejes
1983.
Convexity and Its Applications.
p.
318.
Boltyanskii, V. G. B.
1983.
Combinatorial geometry.
Journal of Soviet Mathematics,
Vol. 23,
Issue. 6,
p.
2753.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.


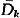 be the density of thinnest
be the density of thinnest