Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T06:23:11.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Tits Triangles

Part of: Other nonassociative rings and algebras Finite geometry and special incidence structures Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  15 November 2018

Bernhard Mühlherr  and
Richard M. Weiss
Bernhard Mühlherr
Affiliation:
Mathematisches Institut, Universität Giessen, 35392 Giessen, Germany Email: bernhard.m.muehlherr@math.uni-giessen.de
Richard M. Weiss
Affiliation:
Department of Mathematics, Tufts University, Medford, MA 02155, USA Email: rweiss@tufts.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Tits polygon is a bipartite graph in which the neighborhood of every vertex is endowed with an “opposition relation” satisfying certain properties. Moufang polygons are precisely the Tits polygons in which these opposition relations are all trivial. There is a standard construction that produces a Tits polygon whose opposition relations are not all trivial from an arbitrary pair 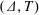$(\unicode[STIX]{x1D6E5},T)$, where 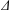$\unicode[STIX]{x1D6E5}$ is a building of type 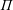$\unicode[STIX]{x1D6F1}$, 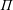$\unicode[STIX]{x1D6F1}$ is a spherical, irreducible Coxeter diagram of rank at least 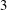$3$, and 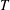$T$ is a Tits index of absolute type 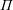$\unicode[STIX]{x1D6F1}$ and relative rank 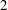$2$. A Tits polygon is called 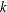$k$-plump if its opposition relations satisfy a mild condition that is satisfied by all Tits triangles coming from a pair 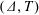$(\unicode[STIX]{x1D6E5},T)$ such that every panel of 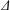$\unicode[STIX]{x1D6E5}$ has at least 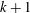$k+1$ chambers. We show that a 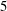$5$-plump Tits triangle is parametrized and uniquely determined by a ring 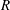$R$ that is alternative and of stable rank 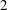$2$. We use the connection between Tits triangles and the theory of Veldkamp planes as developed by Veldkamp and Faulkner to show existence.

Keywords

Tits polygonVeldkamp planebuilding

MSC classification

Primary: 17D05: Alternative rings
Secondary: 20E42: Groups with a $BN$-pair; buildings 51E12: Generalized quadrangles, generalized polygons 51E24: Buildings and the geometry of diagrams
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 3 , September 2019 , pp. 583 - 601
Copyright
© Canadian Mathematical Society 2018 

Footnotes

The work of the first author was partially supported by a grant from the DFG and the work of the second author was partially supported by a collaboration grant from the Simons Foundation.

References

Bass, H., K-theory and stable algebra . Inst. Hautes Études Sci. Publ. Math. 22(1964), 5–60.Google Scholar
Bourbaki, N., Lie groups and Lie algebras. Chapters 4–6 . Springer-Verlag, Berlin, 2002. https://doi.org/10.1007/978-3-540-89394-3.Google Scholar
Drápal, A., A simplified proof of Moufang’s theorem . Proc. Amer. Math. Soc. 139(2011), 93–98. https://doi.org/10.1090/S0002-9939-2010-10501-4.Google Scholar
Faulkner, J. R., Octonion planes defined by quadratic Jordan algebras , Mem. Amer. Math. Soc., 104, American Mathematical Society, Providence, RI, 1970.Google Scholar
Faulkner, J. R., Stable range and linear groups for alternative rings . Geom. Dedicata 14(1983), 177–188. https://doi.org/10.1007/BF00181623.Google Scholar
Faulkner, J. R., Coordinatization of Moufang-Veldkamp planes . Geom. Dedicata 14(1983), 189–201. https://doi.org/10.1007/BF00181624.Google Scholar
Freudenthal, H., Oktaven, Ausnahmegruppen und Oktavengeometrie . Geom. Dedicata 19(1985), 7–63. https://doi.org/10.1007/BF00233101.Google Scholar
Kleinfeld, E., Simple alternative rings . Ann. Math. 58(1953), 544–547. https://doi.org/10.2307/1969753.Google Scholar
Mühlherr, B., Petersson, H. P., and Weiss, R. M., Descent in buildings , Annals of Mathematics Studies, 190, Princeton University Press, Princeton, NJ, 2015. https://doi.org/10.1515/9781400874019.Google Scholar
Mühlherr, B. and Weiss, R. M., Galois involutions and exceptional buildings . Enseign. Math. 62(2016), 207–260. https://doi.org/10.4171/LEM/62-1/2-13.Google Scholar
Mühlherr, B. and Weiss, R. M., Tits polygons . Mem. Amer. Math. Soc., to appear.Google Scholar
Springer, T. A. and Veldkamp, F. D., On Hjelmslev-Moufang planes . Math. Z. 107(1968), 249–263. https://doi.org/10.1007/BF01110014.Google Scholar
Tits, J., Sur la géométrie des R-espaces . J. Math. Pure Appl. 36(1957), 17–38.Google Scholar
Tits, J. and Weiss, R. M., Moufang polygons , Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2002. https://doi.org/10.1007/978-3-662-04689-0.Google Scholar
Veldkamp, F. D., Projective planes over rings of stable rank 2 . Geom. Dedicata 11(1981), 285–308. https://doi.org/10.1007/BF00149352.Google Scholar