Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T00:23:13.467Z Has data issue: false hasContentIssue false
  • English
  • Français

Total Character of a Group G with (G, Z(G)) as a Generalized Camina Pair

Published online by Cambridge University Press:  20 November 2018

S. K. Prajapati  and
R. Sarma
S. K. Prajapati
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, Hauz Khas, New Delhi, 110016, INDIA e-mail: skprajapati.iitd@gmail.com e-mail: ritumoni@maths.iitd.ac.in
R. Sarma
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, Hauz Khas, New Delhi, 110016, INDIA e-mail: skprajapati.iitd@gmail.com e-mail: ritumoni@maths.iitd.ac.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate whether the total character of a finite group $G$ is a polynomial in a suitable irreducible character of $G$ . When 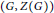$\left( G,\,Z\left( G \right) \right)$ is a generalized Camina pair, we show that the total character is a polynomial in a faithful irreducible character of $G$ if and only if 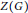$Z\left( G \right)$ is cyclic.

Keywords

20C15finite groupsgroup characterstotal characters
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 2 , 01 June 2016 , pp. 392 - 402
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Berkovich, Y., Groups of prime power order. Vol. 1, de Gruyter Expositions in Mathematics 46, Walter de Gruyter, Berlin, 2008.Google Scholar
[2] Gagola, S. M., Jr. and Lewis, M. L., Squares of characters that are the sum of all irreducible characters. Illinois J. Math. 42(1998), no. 4, 655–672.Google Scholar
[3] Gow, R., Properties of the finite linear group related to the transpose-inverse involution. Proc. London Math. Soc. 47(1983), no. 3, 493–506. http://dx.doi.org/10.1112/plms/s3-47.3.493 Google Scholar
[4] Heffernan, R. and MacHale, D., On the sum of the character degrees of a finite group. Math.Proc. R. Ir. Acad. 108(2008), no. 1, 57–63. http://dx.doi.org/10.3318/PRIA.2008.108.1.57 Google Scholar
[5] Isaacs, I. M., Character theory of finite groups. Pure and Applied Mathematics 69. Academic Press, New York, 2000 Google Scholar
[6] Isaacs, I. M., Loukaki, M., and Moreto, A., The average degree of an irreducible character of a finite group. Israel J. Math. 197(2013), no. 1, 55–67. http://dx.doi.org/10.1007/s11856-013-0013-z Google Scholar
[7] James, G. and Liebeck, M., Representations and characters of groups.Second edition. Cambridge University Press, New York, 2001.Google Scholar
[8] Karpilovsky, G., Group representations. Vol. 1. Part B, In: Introduction to group representations and characters. North-Holland Mathematics Studies, 175.North-Holland, Amsterdam, 1992, pp. i–xiv, 621–1274.Google Scholar
[9] Kodiyalam, V. and Verma, D. N., A natural representation model for symmetric groups. arxiv:math/0402216.Google Scholar
[10] Lemieux, S., Finite exceptional p-groups of small order. Comm. Algebra 35(2007), no. 6, 1890–1894. http://dx.doi.org/10.1080/00927870701246924 Google Scholar
[11] Lewis, M. L., Character tables of groups where all nonlinear irreducible characters vanish off the center. In: Ischia group theory 2008. World Sci. Publ. Hackensack, NJ, 2009, pp. 174–182. http://dx.doi.org/10.1142/9789814277808J3013 Google Scholar
[12] Lewis, M. L., The vanishing-off subgroup. J. Algebra 321(2009), no. 4,1313-1325. http://dx.doi.org/10.1016/j.jalgebra.2008.11.024 Google Scholar
[13] Magaard, K., and Tong-Viet, H. P., Character degree sums infinite nonsolvable groups. J. Group Theory 14(2011), no. 1, 53–57.Google Scholar
[14] Poimenidou, E. and Wolfe, H., Total characters and Chebyshev polynomials.Int. J. Math. Math. Sci.(2003), no. 38, 2447–2453.Google Scholar
[15] Soto-Andrade, J., Geometrical Gelfand models, tensor quotients and Weil epresentations. Proc. Symp.Pure Math.47, Smer.Math.Soc, Providence, RI, 1987, pp. 306–316.Google Scholar
[16] Tong-Viet, H. P., On groups with large character degree sums. Arch. Math. (Basel) 99(2012), no. 5, 401–405. http://dx.doi.org/10.1007/sOOOI3-012-0446-3 Google Scholar
[17] Zhang, J. and Li, X., Finite p-groups all of whose proper subgroups have cyclic Frattini subgroups.J. Group Theory 15(2012), no. 2, 245–259.Google Scholar