Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T02:22:34.670Z Has data issue: false hasContentIssue false
  • English
  • Français

Tracially Quasidiagonal Extensions

Published online by Cambridge University Press:  20 November 2018

Huaxin Lin
Huaxin Lin*
Affiliation:
Department of Mathematics East China Normal University Shanghai China
*
Current address: Department of Mathematics University of Oregon Eugene, Oregon 97403-1222 USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is known that a unital simple 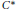${{C}^{*}}$-algebra 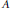$A$ with tracial topological rank zero has real rank zero. We show in this note that, in general, there are unital 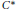${{C}^{*}}$-algebras with tracial topological rank zero that have real rank other than zero.

Let 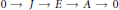$0\,\to \,J\,\to \,E\,\to A\,\to \,0$ be a short exact sequence of 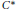${{C}^{*}}$-algebras. Suppose that 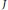$J$ and 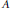$A$ have tracial topological rank zero. It is known that $E$ has tracial topological rank zero as a 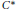${{C}^{*}}$-algebra if and only if $E$ is tracially quasidiagonal as an extension. We present an example of a tracially quasidiagonal extension which is not quasidiagonal.

Keywords

46L0546L80tracially quasidiagonal extensionstracial rank
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 3 , 01 September 2003 , pp. 388 - 399
Copyright
Copyright © Canadian Mathematical Society 2003

Footnotes

Research partially supported by NSF grant DMS 0097903.

References

[BE] Blackadar, B. and Kirchberg, E., Generalized inductive limits of finite dimensional C*-algebras. Math. Ann. 307 (1997), 343–380.Google Scholar
[BD] Brown, N. and Dadarlat, M., Extensions of quasidiagonal C*-algebras and K-theory. Preprint.Google Scholar
[BP] Brown, L. G. and Pedersen, G. K., C*-algebras of real rank zero. J. Funct. Anal. 99 (1991), 131–149.Google Scholar
[Cu1] Cuntz, J., The structure of addition and multiplication in simple C*-algebras. Math. Scand. 40 (1977), 215–233.Google Scholar
[Cu2] Cuntz, J., Dimension function on simple C*-algebras. Math. Ann. 233 (1978), 145–153.Google Scholar
[HLX1] Hu, S., Lin, H. and Xue, Y., The tracial topological rank of C*-algebras (II). Preprint.Google Scholar
[HLX2] Hu, S., Lin, H. and Xue, Y., Tracial topological rank of extensions of C*-algebras. Preprint.Google Scholar
[HLX3] Hu, S., Lin, H. and Xue, Y., K-theory of C*-algebras with finite tracial topological rank. In preparation.Google Scholar
[Ln1] Lin, H., Classification of simple C*-algebras with unique traces. Amer. J. Math. 120 (1998), 1289–1315.Google Scholar
[Ln2] Lin, H., Tracially AF C*-algebras. Trans. Amer. Math. Soc. 353 (2001), 693–722.Google Scholar
[Ln3] Lin, H., Classification of simple tracially AF C*-algebras. Canad. J. Math. 53 (2001), 161–194.Google Scholar
[Ln4] Lin, H., The tracial topological rank of C*-algebras. Proc. LondonMath. Soc. 83 (2001), 199–234.Google Scholar
[Ln5] Lin, H., Classification of simple C*-algebras and higher dimensional tori. Ann. of Math., to appear.Google Scholar
[Ln6] Lin, H., Classification of simple C*-algebras of tracial topological rank zero. MSRI, preprint, 2000.Google Scholar
[S] Salinas, N., Relative quasidiagonality and KK-theory. Houston J. Math. 18 (1992), 97–116.Google Scholar
[Sch] Schochet, C. L., The fine structure of the Kasparov groups II: relative quasidiagonality. Preprint, September 1996.Google Scholar
[Zh] Zhang, S., C*-algebras with real rank zero and the internal structure of their corona and multiplier algebras, III. Canad. J. Math. 42 (1990), 159–190.Google Scholar