Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T13:11:11.741Z Has data issue: false hasContentIssue false
  • English
  • Français

Two Volume Product Inequalities and Their Applications

Published online by Cambridge University Press:  20 November 2018

Alina Stancu
Alina Stancu*
Affiliation:
Department of Mathematics and Statistics, Concordia University, Montréal, QC H3G 1M8 e-mail: stancu@mathstat.concordia.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

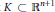Let $K\,\subset \,{{\mathbb{R}}^{n+1}}$ be a convex body of class 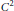${{C}^{2}}$ with everywhere positive Gauss curvature. We show that there exists a positive number 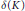$\delta \left( K \right)$ such that for any 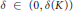$\delta \,\in \,\left( 0,\,\delta \left( K \right) \right)$ we have 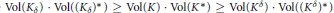$\text{Vol}\left( {{K}_{\delta }} \right)\,\cdot \,\text{Vol}\left( {{\left( {{K}_{\delta }} \right)}^{*}} \right)\,\ge \,\text{Vol}\left( K \right)\,\cdot \,\text{Vol}\left( {{K}^{*}} \right)\,\ge \,\text{Vol}\left( {{K}^{\delta }} \right)\,\cdot \,\text{Vol}\left( {{\left( {{K}^{\delta }} \right)}^{*}} \right)$, where 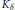${{K}_{\delta }}$, 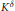${{K}^{\delta }}$ and 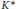${{K}^{*}}$ stand for the convex floating body, the illumination body, and the polar of 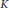$K$, respectively. We derive a few consequences of these inequalities.

Keywords

52A4052A3852A20affine invariantsconvex floating bodiesillumination bodies
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 3 , 01 September 2009 , pp. 464 - 472
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Andrews, B., Evolving convex curves. Calc. Var. Partial Differential Equations 7(1998), 315–371.Google Scholar
[2] Bárány, I. and Vitale, R. A., Random convex hulls: floating bodies and expectations. J. Approx. Theory 75(1993), 130–135.Google Scholar
[3] Buchta, C. and Reitzner, M., Equiaffine inner parallel curves of a plane convex body and the convex hulls of randomly chosen points. Probab. Theory Related Fields 108(1997), 385–415.Google Scholar
[4] Blaschke, W., Über Affine Geometrie VII: Neue Extremeigenschaften von Ellipse und Ellipsoid. Leipziger Ber. 69(1917), 306—318.Google Scholar
[5] Blaschke, W., Vorlesungen über Differentialgeometrie II. Springer-Verlag, Berlin, 1923.Google Scholar
[6] Bourgain, J. and Milman, V. D., New volume ratio properties for convex symmetric bodies in ℝn. Invent. Math. 88(1987), 319–340.Google Scholar
[7] Gordon, Y., Meyer, M., and Reisner, S., Zonoids with minimal volume-product—a new proof. Proc. Amer. Math. Soc. 104(1988), 273–276.Google Scholar
[8] Hug, D., Contributions to affine surface area. Manuscripta Math. 91(1996), 283–301.Google Scholar
[9] Kuperberg, G., A low-technology estimate in convex geometry. Internat. Math. Res. Notices 9(1992), 181–183.Google Scholar
[10] Kuperberg, G., From theMahler conjecture to Gauss linking integrals. Geom. Funct. Anal. 18(2008), 870–892.Google Scholar
[11] Leichtweiss, K., Über ein Formel Blaschkes zur Affinoberfläche. Studia Sci.Math. Hungar. 21(1986), 453–474.Google Scholar
[12] Lopez, M. A. and Reisner, S., A special case ofMahler's conjecture. Discrete Comput. Geom. 20(1998), 163–177.Google Scholar
[13] Ludwig, M. and Reitzner, M., A characterization of affine surface area. Adv. Math. 147(1999), 138–172.Google Scholar
[14] Lutwak, E., Selected affine isoperimetric inequalities. In: Handbook of Convex Geometry, North-Holland, Amsterdam, 1993, pp. 151–176.Google Scholar
[15] Lutwak, E., Extended affine surface area. Adv. Math. 85(1991), 39–68.Google Scholar
[16] Lutwak, E., On the Blaschke-Santaló inequality. Ann. N.Y. Acad. Sci. 440(1985), 106–112.Google Scholar
[17] Lutwak, E. and Zhang, G., Blaschke-Santaló inequalities. J. Differential Geom. 47(1997), 1–16.Google Scholar
[18] Meyer, M. and Werner, E., The Santaló regions of a convex body. Trans. Amer. Math. Soc. 350(1998), 4569–4591.Google Scholar
[19] Meyer, M. and Pajor, A., On Santaló's inequality. In: Geometric Aspects of Functional Analysis, Lecture Notes in Math. 1476, Springer, Berlin, 1989, pp. 261–263.Google Scholar
[20] Meyer, M. and Reisner, S., Characterization of ellipsoids by section-centroid location. Geom. Dedicata 31(1989), 345–355.Google Scholar
[21] Meyer, M. and Reisner, S., A geometric property of the boundary of symmetric convex bodies and convexity of flotation surfaces. Geom. Dedicata 37(1991), 327–337.Google Scholar
[22] Petty, C. M., Affine isoperimetric problems. Ann. New York Acad. Sci. 440(1985), 113–127.Google Scholar
[23] Raymond, J. Saint, Sur le volume des corps convexes symétriques. Initiation à l’analyse, Exp. No. 11, Publ. Math. Univ. Pierre et Marie Curie 46, Univ. Paris VI, Paris, 1981.Google Scholar
[24] Santaló, L. A., Un invariante affine para los cuerpos convexos del espacio de n dimensiones. Portugaliae Math. 8(1949), 155–161.Google Scholar
[25] Schmuckenschläger, M., The distribution function of the convolution square of a convex symmetric body in R n . Israel J. Math. 78(1992), 309–334.Google Scholar
[26] Schneider, R., Convex bodies: The Brunn-Minkowski theory. Encyclopedia of Mathematics and Its Applications 44, Cambridge University Press, Cambridge, 1993.Google Scholar
[27] Schütt, C., The convex floating body and polyhedral approximation. Israel J. Math. 73(1991), 65–77.Google Scholar
[28] Schütt, C., On the affine surface area. Proc. Amer. Math. Soc. 118(1993), 1213–1218.Google Scholar
[29] Schütt, C., Floating body, illumination body, and polytopal approximation. In: Convex Geometric Analysis, Math. Sci. Res. Inst. Publ. 34. Cambridge University Press, Cambridge, 1999, pp. 203–229.Google Scholar
[30] Schütt, C. and Werner, E., The convex floating body. Math. Scand. 66(1990), 275–290.Google Scholar
[31] Stancu, A., The floating body problem. Bull. London Math. Soc. 38(2006), 839–846.Google Scholar
[32] Stancu, A. and Werner, E., New higher-order equiaffine invariants. To appear in Israel J. Math.Google Scholar
[33] Werner, E., Illumination bodies and affine surface area. Studia Math. 110(1994), 257–269.Google Scholar
[34] Werner, E., The p-affine surface area and geometric interpretations. Rend. Circ. Mat. Palermo 70(2002), part II, 367–382.Google Scholar