1 Introduction
En
![]() $1859$
, Bernhard Riemann exposa la fameuse conjecture devenue depuis hypothèse sur le fait que la fonction zeta
$1859$
, Bernhard Riemann exposa la fameuse conjecture devenue depuis hypothèse sur le fait que la fonction zeta
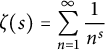 $\zeta (s)=\displaystyle {\sum _{n=1}^{\infty }\frac {1}{n^{s}}}$
avec
$\zeta (s)=\displaystyle {\sum _{n=1}^{\infty }\frac {1}{n^{s}}}$
avec
![]() $\operatorname {Re} (s)>1$
admet, hormis les zéros triviaux, tous ses zéros sur la droite d’équation
$\operatorname {Re} (s)>1$
admet, hormis les zéros triviaux, tous ses zéros sur la droite d’équation
![]() $\operatorname {Re} (s)=\displaystyle {\frac {1}{2}}$
dans le plan complexe.
$\operatorname {Re} (s)=\displaystyle {\frac {1}{2}}$
dans le plan complexe.
L’utilisation des sommes partielles fait partie d’une longue liste de techniques employées en vue de démontrer cette conjecture. Bien que le théorème d’Hurwitz nous dise qu’il est impossible d’utiliser les zéros des sommes partielles pour trouver ceux de la série, on peut attaquer le problème de la localisation des zéros en cherchant les régions du plan complexe où ils ne sont pas.
Un des premiers à avoir employé les sommes partielles de la fonction zeta de Riemann avec l’équivalence de Bohr [Reference Bohr5] fut Turán. Il proposa une relation entre les sommes partielles de la fonction zeta
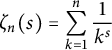 $\zeta _{n}(s)=\displaystyle {\sum _{k=1}^{n}\frac {1}{k^{s}}}$
et l’hypothèse de Riemann. Il déclara que la conjecture de Riemann serait vraie à condition qu’il soit impossible de trouver des zéros des sommes partielles dans le demi-plan ouvert
$\zeta _{n}(s)=\displaystyle {\sum _{k=1}^{n}\frac {1}{k^{s}}}$
et l’hypothèse de Riemann. Il déclara que la conjecture de Riemann serait vraie à condition qu’il soit impossible de trouver des zéros des sommes partielles dans le demi-plan ouvert
![]() $\operatorname {Re} s>1+\displaystyle {\frac {c}{\sqrt {n}}}$
, pour un quelconque
$\operatorname {Re} s>1+\displaystyle {\frac {c}{\sqrt {n}}}$
, pour un quelconque
![]() $c>0$
[Reference Turán23, Theorem I, p. 4]. Il donna un résultat plus précis en disant que les zéros des sommes partielles avec des parties réelles plus grandes que
$c>0$
[Reference Turán23, Theorem I, p. 4]. Il donna un résultat plus précis en disant que les zéros des sommes partielles avec des parties réelles plus grandes que
![]() $1+N^{-\frac {1}{2}+\epsilon }$
n’existent pas. Il fut démontré, en
$1+N^{-\frac {1}{2}+\epsilon }$
n’existent pas. Il fut démontré, en
![]() $1983$
, par Montgomery dans [Reference Montgomery13] que cette conjecture est fausse.
$1983$
, par Montgomery dans [Reference Montgomery13] que cette conjecture est fausse.
Parmi les nombreux auteurs qui travaillèrent avec les sommes partielles de la fonction zeta de Riemann, on peut citer Spira [Reference Spira20–Reference Spira22]. Il utilisa, lui-aussi, le théorème d’équivalence de Bohr comme outil pour étudier la distribution des zéros de
![]() $\zeta _{n}(s)$
, il exposa, dans [Reference Spira21], comme conjecture, la possibilité que les parties réelles des zéros de
$\zeta _{n}(s)$
, il exposa, dans [Reference Spira21], comme conjecture, la possibilité que les parties réelles des zéros de
![]() $\zeta _{n}(z)$
soient denses dans certains intervalles inclus dans leurs bandes critiques respectives.
$\zeta _{n}(z)$
soient denses dans certains intervalles inclus dans leurs bandes critiques respectives.
Une réponse partielle à cette conjecture fut publiée par C. Moreno dans [Reference Moreno17] où il montra qu’effectivement il y avait bien densité des parties réelles des zéros de cas particuliers de sommes partielles:
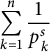 $\displaystyle {\sum _{k=1}^{n}\frac {1}{p^{s}_{k}}}$
où les
$\displaystyle {\sum _{k=1}^{n}\frac {1}{p^{s}_{k}}}$
où les
![]() $p_{k}$
représentent les n premiers nombres premiers. Il aborda le thème de densité en disant que l’on peut trouver des zéros de ces sommes partielles, dans la bande critique, proches de n’importe quelle droite perpendiculaire à l’axe des abscisses.
$p_{k}$
représentent les n premiers nombres premiers. Il aborda le thème de densité en disant que l’on peut trouver des zéros de ces sommes partielles, dans la bande critique, proches de n’importe quelle droite perpendiculaire à l’axe des abscisses.
Ce résultat fut généralisé dans [Reference Dubon, Mora, Sepulcre, Ubeda and Vidal6] pour
![]() $\zeta _{n}(s)$
dans le cas où n est premier puis pour un n quelconque dans [Reference Mora15].
$\zeta _{n}(s)$
dans le cas où n est premier puis pour un n quelconque dans [Reference Mora15].
L′étude des zéros des sommes partielles représente toujours un angle d’attaque de la conjecture de Riemann voir, par exemple, [Reference Gonek and Montgomery8] et sert à mieux comprendre la répartition des zéros des fonctions L de Dirichlet de façon plus générale voir, par exemple, [Reference Li, Roy and Zaharescu11–Reference Roy and Vatwani18].
Richard Dedekind proposa une généralisation de la fonction zeta de Riemann en introduisant la fonction zeta de Dedekind associée à un corps de nombres K de degré
![]() $d=[K:\mathbb {Q}]$
.
$d=[K:\mathbb {Q}]$
.
Cette fonction est définie, elle-aussi, pour
![]() $\operatorname {Re} (s)>1$
par
$\operatorname {Re} (s)>1$
par
 $$ \begin{align*} \zeta_{K}(s)=\sum_{\mathfrak{a}\subset \mathcal{O}_{K}}\frac{1}{N(\mathfrak{a})^{s}}=\displaystyle{\prod_{\mathfrak{p}\subset\mathcal{O}_{K}}} (1-N(\mathfrak{p})^{-s})^{-1} \end{align*} $$
$$ \begin{align*} \zeta_{K}(s)=\sum_{\mathfrak{a}\subset \mathcal{O}_{K}}\frac{1}{N(\mathfrak{a})^{s}}=\displaystyle{\prod_{\mathfrak{p}\subset\mathcal{O}_{K}}} (1-N(\mathfrak{p})^{-s})^{-1} \end{align*} $$
où la somme est prise pour tous les idéaux entiers non nuls de
![]() $\mathcal {O}_{K}$
,
$\mathcal {O}_{K}$
,
![]() $\mathfrak {p}$
appartient à l’ensemble des idéaux premiers et
$\mathfrak {p}$
appartient à l’ensemble des idéaux premiers et
![]() $N(\mathfrak {a})$
désigne la norme absolue de l’idéal
$N(\mathfrak {a})$
désigne la norme absolue de l’idéal
![]() $\mathfrak {a}$
.
$\mathfrak {a}$
.
Dans le cas particulier où
![]() $K=\mathbb {Q}$
alors on retrouve la fonction zeta de Riemann.
$K=\mathbb {Q}$
alors on retrouve la fonction zeta de Riemann.
On sait très peu de choses concernant la répartition des zéros des sommes partielles de la fonction zeta de Dedekind.
En
![]() $2014$
, Ledoan et al., dans [Reference Ledoan, Roy and Zaharescu10, Lemma 1, p. 120], démontrèrent que:
$2014$
, Ledoan et al., dans [Reference Ledoan, Roy and Zaharescu10, Lemma 1, p. 120], démontrèrent que:
“Si K est un corps de nombres algébriques de degré
![]() $n_{0}=[K:\mathbb {Q}]$
sur le corps des nombres rationnels. Soit
$n_{0}=[K:\mathbb {Q}]$
sur le corps des nombres rationnels. Soit
![]() $n\geq 2$
et soit
$n\geq 2$
et soit
![]() $s=\sigma +it$
un nombre complexe alors existent deux réels
$s=\sigma +it$
un nombre complexe alors existent deux réels
![]() $\alpha $
et
$\alpha $
et
![]() $\beta $
avec
$\beta $
avec
![]() $\alpha $
dépendant de
$\alpha $
dépendant de
![]() $n_{0}$
et n seulement et
$n_{0}$
et n seulement et
![]() $\beta $
dépendant uniquement de n tels que les zéros des sommes partielles de la zeta de Dedekind sont tous contenus dans des bandes verticales du plan complexe définies par
$\beta $
dépendant uniquement de n tels que les zéros des sommes partielles de la zeta de Dedekind sont tous contenus dans des bandes verticales du plan complexe définies par
![]() $\alpha < \sigma <\beta $
.”
$\alpha < \sigma <\beta $
.”
Nous considérons, ici, la fonction zeta de Dedekind définie sur un corps quadratique et nous prétendons démontrer, en nous basant sur l’équivalence au sens de Bohr voir [Reference Apostol3] et sur l’article [Reference Dubon and Sepulcre7], que les zéros de ses sommes partielles vérifient une propriété de densité analogue à celle énoncée précédemment.
2 Équivalence au sens de Bohr, sommes partielles de la zeta de Dedekind et densité
Afin de pouvoir démontrer le résultat principal de cette note, nous avons besoin de nous appuyer sur des résultats de [Reference Dubon and Sepulcre7] que nous présentons ici sous forme de Lemmes.
Les exponentielles-polynômes dont les polynômes de Dirichlet sont des cas particulier peuvent être écrites sous la forme
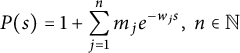 $$ \begin{align} P(s)=1+\sum_{j=1}^{n}m_{j}e^{-w_js},\ n\in\mathbb{N} \end{align} $$
$$ \begin{align} P(s)=1+\sum_{j=1}^{n}m_{j}e^{-w_js},\ n\in\mathbb{N} \end{align} $$
avec
![]() $w_1 < \cdots <w_n$
strictement positifs et
$w_1 < \cdots <w_n$
strictement positifs et
![]() $m_j\in \mathbb {C}\setminus \{0\}$
,
$m_j\in \mathbb {C}\setminus \{0\}$
,
![]() $j=1,\ldots ,n$
.
$j=1,\ldots ,n$
.
Considérons deux polynômes de Dirichlet de la forme (2.1) ayant le même ensemble d’exposants
![]() $\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _n\}$
:
$\Lambda =\{\lambda _1,\lambda _2,\ldots ,\lambda _n\}$
:
Si
![]() $B=\{\beta _1,\beta _2,\ldots ,\beta _{q_n}\}$
, où
$B=\{\beta _1,\beta _2,\ldots ,\beta _{q_n}\}$
, où
![]() $q_n$
dépend de n, est une base pour
$q_n$
dépend de n, est une base pour
![]() $\Lambda $
alors, pour chaque
$\Lambda $
alors, pour chaque
![]() $m=1,2,\ldots ,n$
, on a
$m=1,2,\ldots ,n$
, on a
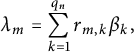 $$ \begin{align} \lambda_{m}=\sum_{k=1}^{q_n}r_{m,k}\beta_k, \end{align} $$
$$ \begin{align} \lambda_{m}=\sum_{k=1}^{q_n}r_{m,k}\beta_k, \end{align} $$
où
![]() $r_{m,k}$
sont des nombres rationnels.
$r_{m,k}$
sont des nombres rationnels.
Definition 2.1 Deux polynômes de Dirichlet
![]() $f(s)=1+\sum _{m=1}^{n}a_{m}e^{-\lambda _{m}s}$
et
$f(s)=1+\sum _{m=1}^{n}a_{m}e^{-\lambda _{m}s}$
et
![]() $g(s)=1+\sum _{m=1}^{n}b_{m}e^{-\lambda _{m}s}$
de type (2.1) avec le même ensemble d’exposants sont dits équivalents au sens de Bohr, relativement à la base
$g(s)=1+\sum _{m=1}^{n}b_{m}e^{-\lambda _{m}s}$
de type (2.1) avec le même ensemble d’exposants sont dits équivalents au sens de Bohr, relativement à la base
![]() $\{\beta _1,\beta _2,\ldots ,\beta _{q_n}\}$
, si pour un certain ensemble de nombres réels
$\{\beta _1,\beta _2,\ldots ,\beta _{q_n}\}$
, si pour un certain ensemble de nombres réels
![]() $Y=\{y_{1},y_2,\ldots ,y_{q_n}\}$
on obtient
$Y=\{y_{1},y_2,\ldots ,y_{q_n}\}$
on obtient
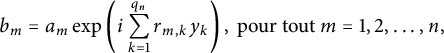 $$ \begin{align*} b_{m}=a_{m}\operatorname{exp}\left(i\sum_{k=1}^{q_n}r_{m,k}y_{k}\right),\ \mbox{pour tout }m=1,2,\ldots,n, \end{align*} $$
$$ \begin{align*} b_{m}=a_{m}\operatorname{exp}\left(i\sum_{k=1}^{q_n}r_{m,k}y_{k}\right),\ \mbox{pour tout }m=1,2,\ldots,n, \end{align*} $$
où les
![]() $r_{m,k}$
vérifient (2.2).
$r_{m,k}$
vérifient (2.2).
La définition précédente constitue un cas particulier de l’équivalence au sens de Bohr pour les séries de Dirichlet (voir [Reference Apostol2, p. 173]). Il s’agit bien d’une relation d’équivalence qui est indépendante de la base choisie. Pour plus d’informations à ce sujet voir [Reference Apostol2, Theorems 8.10 et 8.11]).
Lemme 2.1 ([Reference Dubon and Sepulcre7, Proposition 2.2])
Deux polynômes de Dirichlet ordinaires,
sont dits équivalents au sens de Bohr si et seulement si, il existe une fonction
![]() $\chi :\{1,2,\ldots ,n\}\rightarrow \mathbb {C}$
telle que
$\chi :\{1,2,\ldots ,n\}\rightarrow \mathbb {C}$
telle que
-
(i)
 $\chi (1)=1$
et
$\chi (1)=1$
et
 $\chi (ml)=\chi (m)\chi (l)$
pour tous entiers naturels m et l tels que
$\chi (ml)=\chi (m)\chi (l)$
pour tous entiers naturels m et l tels que
 $ml\leq n$
;
$ml\leq n$
; -
(ii)
 $b_{m}=\chi (m)a_{m}$
pour chaque
$b_{m}=\chi (m)a_{m}$
pour chaque
 $m=2,\ldots ,n$
;
$m=2,\ldots ,n$
; -
(iii)
 $|\chi (p)|=1$
à condition que
$|\chi (p)|=1$
à condition que
 $a_{m}\not =0$
et p soit un diviseur premier de m.
$a_{m}\not =0$
et p soit un diviseur premier de m.
Étant donné un polynôme de Dirichlet ordinaire
![]() $\displaystyle {P(s)=1+\sum _{m=2}^{n}a_{m}m^{-s}}$
, il est un fait connu que tous ses zéros sont situés dans une bande verticale du plan complexe appelée bande critique de
$\displaystyle {P(s)=1+\sum _{m=2}^{n}a_{m}m^{-s}}$
, il est un fait connu que tous ses zéros sont situés dans une bande verticale du plan complexe appelée bande critique de
![]() $P(s)$
, bornée par les réels
$P(s)$
, bornée par les réels
![]() $\alpha _{P}$
et
$\alpha _{P}$
et
![]() $ \beta _{P}$
, où
$ \beta _{P}$
, où
![]() $\alpha _{P}:= \inf \left \{ \operatorname {Re}s:P(s)=0\right \}$
et
$\alpha _{P}:= \inf \left \{ \operatorname {Re}s:P(s)=0\right \}$
et
![]() $\beta _{P}:= \sup \left \{ \operatorname {Re}s:P(s)=0\right \}$
. Ces bornes nous permettent de définir un intervalle
$\beta _{P}:= \sup \left \{ \operatorname {Re}s:P(s)=0\right \}$
. Ces bornes nous permettent de définir un intervalle
![]() $I_{P}:= \left [ \alpha _{P},\beta _{P}\right ]$
, appelé intervalle critique de
$I_{P}:= \left [ \alpha _{P},\beta _{P}\right ]$
, appelé intervalle critique de
![]() $P(s)$
.
$P(s)$
.
Et, finalement, associé à
![]() $P(s)$
, nous considèrerons l’ensemble
$P(s)$
, nous considèrerons l’ensemble
Lemme 2.2 ([Reference Dubon and Sepulcre7, Theorem 3.1])
Soient
![]() $P(s)=1+\sum _{m=2}^{n}a_{m}m^{-s} \mbox { et } Q(s)=1+\sum _{m=2}^{n}b_{m}m^{-s}$
deux polynômes de Dirichlet ordinaires équivalents au sens de Bohr, alors
$P(s)=1+\sum _{m=2}^{n}a_{m}m^{-s} \mbox { et } Q(s)=1+\sum _{m=2}^{n}b_{m}m^{-s}$
deux polynômes de Dirichlet ordinaires équivalents au sens de Bohr, alors
![]() $R_P=R_Q$
.
$R_P=R_Q$
.
Definition 2.2 (Propriété de densité)
Soit
![]() $S_{(a,b)}\equiv \left \{ s\in \mathbb {C} :a < \operatorname {Re}s < b\right \}$
une bande ouverte verticale du plan complexe contenue dans la bande critique d’un polynôme de Dirichlet
$S_{(a,b)}\equiv \left \{ s\in \mathbb {C} :a < \operatorname {Re}s < b\right \}$
une bande ouverte verticale du plan complexe contenue dans la bande critique d’un polynôme de Dirichlet
![]() $P(s)$
. Nous dirons que
$P(s)$
. Nous dirons que
![]() $P(s)$
possède la propriété de densité dans la bande
$P(s)$
possède la propriété de densité dans la bande
![]() $S_{(a,b)}$
à chaque fois qu’il possèdera des zéros situés arbitrairement proches de n’importe quelle droite verticale située dans la bande
$S_{(a,b)}$
à chaque fois qu’il possèdera des zéros situés arbitrairement proches de n’importe quelle droite verticale située dans la bande
![]() $S_{(a,b)}$
. Autrement dit, étant donné
$S_{(a,b)}$
. Autrement dit, étant donné
![]() $\sigma _2$
avec
$\sigma _2$
avec
![]() $a < \sigma _2<b$
et
$a < \sigma _2<b$
et
![]() $\varepsilon>0$
, un nombre complexe
$\varepsilon>0$
, un nombre complexe
![]() $s^{*}=\sigma ^{*}+it^{*}$
peut être trouvé de façon à ce que
$s^{*}=\sigma ^{*}+it^{*}$
peut être trouvé de façon à ce que
![]() $\sigma _2-\varepsilon < \sigma ^{*} < \sigma _2+\varepsilon $
et
$\sigma _2-\varepsilon < \sigma ^{*} < \sigma _2+\varepsilon $
et
![]() $P(s^{*})=0$
.
$P(s^{*})=0$
.
De manière équivalente, nous pouvons remarquer que si
![]() $P(s)$
est un polynôme de Dirichlet qui a la propriété de densité dans la bande
$P(s)$
est un polynôme de Dirichlet qui a la propriété de densité dans la bande
![]() $S_{(a,b)}$
, alors cela signifie que l’ensemble
$S_{(a,b)}$
, alors cela signifie que l’ensemble
![]() $\{\operatorname {Re}s:P(s)=0\}$
est dense dans l’intervalle
$\{\operatorname {Re}s:P(s)=0\}$
est dense dans l’intervalle
![]() $[a,b]$
, c’est à dire,
$[a,b]$
, c’est à dire,
![]() $R_P=[a,b]$
. Nous avons donc le résultat suivant:
$R_P=[a,b]$
. Nous avons donc le résultat suivant:
Lemme 2.3 ([Reference Dubon and Sepulcre7, Corollary 3.4])
Soit
![]() $S_{(a,b)}$
une bande verticale ouverte dans le plan complexe dans laquelle les polynômes de Dirichlet ordinaires
$S_{(a,b)}$
une bande verticale ouverte dans le plan complexe dans laquelle les polynômes de Dirichlet ordinaires
![]() $P(s)$
possèdent la propriété de densité. Si
$P(s)$
possèdent la propriété de densité. Si
![]() $Q(s)$
est un autre polynôme de Dirichlet ordinaire de telle sorte que
$Q(s)$
est un autre polynôme de Dirichlet ordinaire de telle sorte que
![]() $P(s)$
et
$P(s)$
et
![]() $Q(s)$
sont tous les deux équivalents au sens de Bohr, alors
$Q(s)$
sont tous les deux équivalents au sens de Bohr, alors
![]() $Q(s)$
a, lui-aussi, la propriété de densité dans la bande
$Q(s)$
a, lui-aussi, la propriété de densité dans la bande
![]() $S_{(a,b)}$
.
$S_{(a,b)}$
.
Venons en, maintenant, à la fonction zeta de Dedekind.
On sait d’après la formule de factorisation de Kronecker appliquée à un corps quadratique
![]() $K=\mathbb {Q}(\sqrt {D})$
(voir [Reference Iwaniec and Kowalski9, p. 513]) que la fonction zeta de Dedekind s’écrit comme produit de la fonction zeta de Riemann et d’une fonction L.
$K=\mathbb {Q}(\sqrt {D})$
(voir [Reference Iwaniec and Kowalski9, p. 513]) que la fonction zeta de Dedekind s’écrit comme produit de la fonction zeta de Riemann et d’une fonction L.
Autrement dit:
où
![]() $\chi _{D}$
est un caractère quadratique associé au discriminant, le symbole de Kronecker.
$\chi _{D}$
est un caractère quadratique associé au discriminant, le symbole de Kronecker.
On obtient alors par le produit de convolution de Dirichlet [Reference Iwaniec and Kowalski9, p. 12] que:
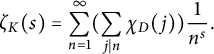 $$ \begin{align*}\zeta_{K}(s)=\sum_{n=1}^{\infty}(\sum_{j|n}\chi_{D}(j))\frac{1}{n^{s}}.\end{align*} $$
$$ \begin{align*}\zeta_{K}(s)=\sum_{n=1}^{\infty}(\sum_{j|n}\chi_{D}(j))\frac{1}{n^{s}}.\end{align*} $$
On note alors les sommes partielles de la forme suivante:
 $$ \begin{align*}\zeta_{K,n}(s)=\sum_{k=1}^{n}\frac{f(k)}{k^{s}} \mbox{ avec } \operatorname {Re} (s)>1, \ n\in\mathbb{N} \mbox{ et } f(k)=\sum_{j|k}\chi_{D}(j) \quad \forall k=1,...,n.\end{align*} $$
$$ \begin{align*}\zeta_{K,n}(s)=\sum_{k=1}^{n}\frac{f(k)}{k^{s}} \mbox{ avec } \operatorname {Re} (s)>1, \ n\in\mathbb{N} \mbox{ et } f(k)=\sum_{j|k}\chi_{D}(j) \quad \forall k=1,...,n.\end{align*} $$
Nous présentons maintenant le résultat principal de cette note.
Théorème 2.4 Soit K un corps quadratique de discriminant D. Soit, pour tout n entier naturel,
![]() $\zeta _{K,n}$
les sommes partielles de la fonction zeta de Dedekind définies sur K. Si
$\zeta _{K,n}$
les sommes partielles de la fonction zeta de Dedekind définies sur K. Si
![]() $f(k)$
est une fonction complètement multiplicative vérifiant les conditions du lemme
2.1
alors les sommes partielles
$f(k)$
est une fonction complètement multiplicative vérifiant les conditions du lemme
2.1
alors les sommes partielles
![]() $\zeta _{K,n}$
ont leurs zéros dans des bandes verticales du plan complexe et les parties réelles de ceux-ci y sont denses.
$\zeta _{K,n}$
ont leurs zéros dans des bandes verticales du plan complexe et les parties réelles de ceux-ci y sont denses.
Démonstration Si D est un discriminant tel que
![]() $f(k)$
est une fonction complètement multiplicative vérifiant le lemme 2.1 alors nous pouvons dire que
$f(k)$
est une fonction complètement multiplicative vérifiant le lemme 2.1 alors nous pouvons dire que
![]() $\zeta _{K,n}(s)$
est équivalente au sens de Bohr à
$\zeta _{K,n}(s)$
est équivalente au sens de Bohr à
![]() $\zeta _{n}(s) $
somme partielle de la fonction zeta de Riemman. Or nous savons d’après [Reference Mora15, Theorem 12] qu’il existe un entier N tel que pour tout n strictement plus grand que N, les sommes partielles de la zeta de Riemann possèdent tous leurs zéros dans une bande verticale du plan complexe appelée bande critique
$\zeta _{n}(s) $
somme partielle de la fonction zeta de Riemman. Or nous savons d’après [Reference Mora15, Theorem 12] qu’il existe un entier N tel que pour tout n strictement plus grand que N, les sommes partielles de la zeta de Riemann possèdent tous leurs zéros dans une bande verticale du plan complexe appelée bande critique
![]() $S_{(a_{n},b_{n})}$
où
$S_{(a_{n},b_{n})}$
où
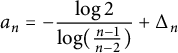 $a_{n}=\displaystyle {-\frac {\log 2}{\log (\frac {n-1}{n-2})}+\Delta _{n}}$
pour
$a_{n}=\displaystyle {-\frac {\log 2}{\log (\frac {n-1}{n-2})}+\Delta _{n}}$
pour
![]() $n>2$
avec
$n>2$
avec
![]() $\displaystyle {\limsup _{n\rightarrow \infty }|\Delta _{n}|\leq \log 2}$
(voir pour cela [Reference Mora16]) et
$\displaystyle {\limsup _{n\rightarrow \infty }|\Delta _{n}|\leq \log 2}$
(voir pour cela [Reference Mora16]) et
![]() $b_{n}=\displaystyle {1+(\frac {4}{\pi }-1+o(1))\frac {\log \log n}{\log n}}, \ n\rightarrow \infty $
estimation trouvée par Montgomery et Vaughan dans [Reference Montgomery and Vaughan14]. De plus, nous savons, voir [Reference Dubon, Mora, Sepulcre, Ubeda and Vidal6, Reference Mora15] que
$b_{n}=\displaystyle {1+(\frac {4}{\pi }-1+o(1))\frac {\log \log n}{\log n}}, \ n\rightarrow \infty $
estimation trouvée par Montgomery et Vaughan dans [Reference Montgomery and Vaughan14]. De plus, nous savons, voir [Reference Dubon, Mora, Sepulcre, Ubeda and Vidal6, Reference Mora15] que
![]() $\zeta _{n}(s) $
y possède la propriété de densité. En utilisant alors les lemmes 2.2 et 2.3, on obtient le résultat voulu.
$\zeta _{n}(s) $
y possède la propriété de densité. En utilisant alors les lemmes 2.2 et 2.3, on obtient le résultat voulu.
Remarque 2.5 Dans un article récent [Reference Roy and Vatwani19], Roy et Vatwani considèrent le cas de séries de Dirichlet
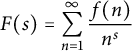 $F(s)=\displaystyle {\sum _{n=1}^{\infty }\frac {f(n)}{n^{s}}}$
où
$F(s)=\displaystyle {\sum _{n=1}^{\infty }\frac {f(n)}{n^{s}}}$
où
![]() $f:\mathbb {N}\rightarrow \mathbb {C}$
est une fonction arithmétique appartenant à une sous-famille
$f:\mathbb {N}\rightarrow \mathbb {C}$
est une fonction arithmétique appartenant à une sous-famille
![]() $\mathcal {C}_{k}$
(introduite dans [Reference Roy and Vatwani18]) de fonctions multiplicatives pour lesquelles les séries de Dirichlet précédentes sont absolument convergentes pour
$\mathcal {C}_{k}$
(introduite dans [Reference Roy and Vatwani18]) de fonctions multiplicatives pour lesquelles les séries de Dirichlet précédentes sont absolument convergentes pour
![]() $\operatorname {Re} (s)>1$
.
$\operatorname {Re} (s)>1$
.
Ils y démontrent, dans le cas des sommes partielles des
![]() $F(s)$
, un résultat généralisant l’expression de la borne supérieure
$F(s)$
, un résultat généralisant l’expression de la borne supérieure
![]() $b_{n}$
trouvée par Montgomery et Vaughan pour les sommes partielles de la zeta de Riemann.
$b_{n}$
trouvée par Montgomery et Vaughan pour les sommes partielles de la zeta de Riemann.
Corollaire 2.6 Soit K un corps quadratique de discriminant noté D. Si pour tout nombre premier p impair ne divisant pas le discriminant nous avons ce dernier qui n’est pas congru à un carré modulo p et si pour p pair, D n’est pas congru à
![]() $1$
modulo
$1$
modulo
![]() $8$
.
$8$
.
Alors les sommes partielles de la fonction zeta de Dedekind ont leurs zéros situés dans une bande verticale du plan complexe et elles y possèdent la propriété de densité.
Démonstration Nous avons vu que
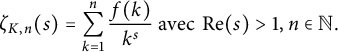 $$ \begin{align*}\zeta_{K,n}(s)=\sum_{k=1}^{n}\frac{f(k)}{k^{s}} \mbox{ avec } \operatorname {Re} (s)>1, n\in\mathbb{N}.\end{align*} $$
$$ \begin{align*}\zeta_{K,n}(s)=\sum_{k=1}^{n}\frac{f(k)}{k^{s}} \mbox{ avec } \operatorname {Re} (s)>1, n\in\mathbb{N}.\end{align*} $$
où
![]() $f(k)=\displaystyle {\sum _{j|k}}\chi _{D}(j)$
est obtenu grâce au produit de convolution de Dirichlet. Si l’on souhaite connaître les valeurs prises par
$f(k)=\displaystyle {\sum _{j|k}}\chi _{D}(j)$
est obtenu grâce au produit de convolution de Dirichlet. Si l’on souhaite connaître les valeurs prises par
![]() $f(k)$
pour tout
$f(k)$
pour tout
![]() $k=1,...,n$
, il suffit alors de s’intéresser uniquement aux puissances de nombres premiers.
$k=1,...,n$
, il suffit alors de s’intéresser uniquement aux puissances de nombres premiers.
Le fait que D ne soit pas congru à un carré modulo p implique que si p est un nombre premier impair ne divisant pas D alors l’idéal engendré par p noté
![]() $(p)$
est soit inerte soit ramifié. De plus, le fait que
$(p)$
est soit inerte soit ramifié. De plus, le fait que
![]() $D\not \equiv 1(8)$
implique que si p est pair alors
$D\not \equiv 1(8)$
implique que si p est pair alors
![]() $(p)$
est aussi inerte ( pour D
$(p)$
est aussi inerte ( pour D
![]() $\equiv 5(8)$
) ou ramifié. Ce qui se traduit par le fait que pour tout nombre premier p nous avons
$\equiv 5(8)$
) ou ramifié. Ce qui se traduit par le fait que pour tout nombre premier p nous avons
![]() $\chi _{D}(p)\not =1$
. Nous pouvons alors écrire (voir [Reference Blomer and Granville4]):
$\chi _{D}(p)\not =1$
. Nous pouvons alors écrire (voir [Reference Blomer and Granville4]):
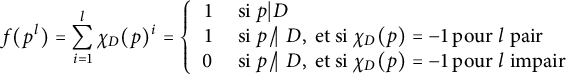 $$ \begin{align*}f(p^{l})=\sum_{i=1}^{l}\chi_{D}(p)^{i}=\left\{ \begin{array}{rl} 1 & \mbox{ si } p|D \\ 1 & \mbox{ si } p\kern1pt /\kern-4.6pt \mid \kern1pt D, \mbox{ et si } \chi_{D}(p) =-1 \mbox{ pour } l \mbox{ pair }\\ 0 & \mbox{ si } p\kern1pt /\kern-4.6pt\mid\kern1pt D, \mbox{ et si } \chi_{D}(p) =-1 \mbox{ pour } l \mbox{ impair } \end{array} \right.\end{align*} $$
$$ \begin{align*}f(p^{l})=\sum_{i=1}^{l}\chi_{D}(p)^{i}=\left\{ \begin{array}{rl} 1 & \mbox{ si } p|D \\ 1 & \mbox{ si } p\kern1pt /\kern-4.6pt \mid \kern1pt D, \mbox{ et si } \chi_{D}(p) =-1 \mbox{ pour } l \mbox{ pair }\\ 0 & \mbox{ si } p\kern1pt /\kern-4.6pt\mid\kern1pt D, \mbox{ et si } \chi_{D}(p) =-1 \mbox{ pour } l \mbox{ impair } \end{array} \right.\end{align*} $$
Dans ces conditions, on a, pour tout entier l,
![]() $f(p^{l})=f(p)^{l}$
ce qui permet de conclure (voir [Reference Apostol2, p. 266]) que, dans ce cas, f est une fonction complètement multiplicative vérifiant les conditions du lemme 2.1 et nous obtenons le résultat grâce au théorème 2.4.
$f(p^{l})=f(p)^{l}$
ce qui permet de conclure (voir [Reference Apostol2, p. 266]) que, dans ce cas, f est une fonction complètement multiplicative vérifiant les conditions du lemme 2.1 et nous obtenons le résultat grâce au théorème 2.4.
Remarque 2.7 Le fait que la fonction f considérée dans le corollaire 2.6 soit complètement multiplicative repose sur les propriétés du caractère quadratique et le fait que lui-même, dans les conditions imposées du corollaire, est une fonction complètement multiplicative en tant que caractère de Dirichlet.
Par contre, si D est congru à
![]() $3$
modulo
$3$
modulo
![]() $4$
alors le symbole de Kronecker n’est pas un caractère de Dirichlet. Cependant il conserve toutes les propriétés nécessaires à la véracité du théorème puisque si D est congru à
$4$
alors le symbole de Kronecker n’est pas un caractère de Dirichlet. Cependant il conserve toutes les propriétés nécessaires à la véracité du théorème puisque si D est congru à
![]() $3$
modulo
$3$
modulo
![]() $4$
alors le symbole de Kronecker est un “mock” caractère [Reference Allouche and Goldmakher1, Theorem 3.6, p. 367] tel qu’il est défini dans [Reference Allouche and Goldmakher1, Definition 2.4, p. 360] et continue de vérifier les conditions du Lemme 2.1.
$4$
alors le symbole de Kronecker est un “mock” caractère [Reference Allouche and Goldmakher1, Theorem 3.6, p. 367] tel qu’il est défini dans [Reference Allouche and Goldmakher1, Definition 2.4, p. 360] et continue de vérifier les conditions du Lemme 2.1.
Remerciements
Je remercie vivement le rapporteur de ce travail pour ses commentaires très utiles qui ont permis d’améliorer cet article.



