Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T03:15:18.241Z Has data issue: false hasContentIssue false
  • English
  • Français

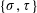$\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter Operators, Infinitesimal Hom-bialgebras and the Associative (Bi)Hom-Yang–Baxter Equation

Part of: Other nonassociative rings and algebras General nonassociative rings Basic linear algebra

Published online by Cambridge University Press:  07 January 2019

Ling Liu ,
Abdenacer Makhlouf ,
Claudia Menini  and
Florin Panaite
Ling Liu
Affiliation:
College of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua, 321004, China Email: ntliulin@zjnu.cn
Abdenacer Makhlouf
Affiliation:
Université de Haute Alsace, IRIMAS - département de Mathématiques, F-68093 Mulhouse, France Email: abdenacer.makhlouf@uha.fr
Claudia Menini
Affiliation:
University of Ferrara, Department of Mathematics and Computer Science, via Machiavelli, I-44121 Ferrara, Italy Email: men@unife.it
Florin Panaite
Affiliation:
Institute of Mathematics of the Romanian Academy, PO-Box 1-764, RO-014700 Bucharest, Romania Email: florin.panaite@imar.ro
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

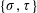We introduce the concept of a $\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter operator, as a twisted version of a Rota–Baxter operator of weight zero. We show how to obtain a certain 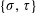$\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter operator from a solution of the associative (Bi)Hom-Yang–Baxter equation, and, in a compatible way, a Hom-pre-Lie algebra from an infinitesimal Hom-bialgebra.

Keywords

Rota–Baxter operatorHom-pre-Lie algebrainfinitesimal Hom-bialgebraassociative (Bi)Hom-Yang–Baxter equation

MSC classification

Primary: 15A04: Linear transformations, semilinear transformations
Secondary: 17A99: None of the above, but in this section 17D99: None of the above, but in this section
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 2 , June 2019 , pp. 355 - 372
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Author L. L. was supported by NSFC (Grant No.11601486) and Foundation of Zhejiang Educational Committee (Y201738645). This paper was written while Author C. M. was a member of the National Group for Algebraic and Geometric Structures and their Applications (GNSAGA-INdAM).

References

Aguiar, M., Pre-Poisson algebras . Lett. Math. Phys. 54(2000), 263–277. https://doi.org/10.1023/A:1010818119040.Google Scholar
Aguiar, M., Infinitesimal Hopf algebras . In: New trends in Hopf algebra theory (La Falda, 1999), Contemp. Math., 267, American Mathematical Society, Providence, RI, 2000, pp. 1–29. https://doi.org/10.1090/conm/267/04262.Google Scholar
Aguiar, M., On the associative analog of Lie bialgebras . J. Algebra 244(2001), no. 2, 492–532. https://doi.org/10.1006/jabr.2001.8877.Google Scholar
Aguiar, M., Infinitesimal bialgebras, pre-Lie and dendriform algebras . In: Hopf algebras, Lecture Notes in Pure and Appl. Math., 237, Dekker, New York, 2004, pp. 1–33.Google Scholar
Brzeziński, T., Rota–Baxter systems, dendriform algebras and covariant bialgebras . J. Algebra 460(2016), 1–25. https://doi.org/10.1016/j.jalgebra.2016.04.018.Google Scholar
Connes, A. and Kreimer, D., Hopf algebras, renormalization and noncommutative geometry . Comm. Math. Phys. 199(1998), no. 1, 203–242. https://doi.org/10.1007/s002200050499.Google Scholar
Ebrahimi-Fard, K. and Manchon, D., Twisted dendriform algebras and the pre-Lie Magnus expansion . J. Pure Appl. Algebra 215(2011), 2615–2627. https://doi.org/10.1016/j.jpaa.2011.03.004.Google Scholar
Graziani, G., Makhlouf, A., Menini, C., and Panaite, F., BiHom-associative algebras, BiHom-Lie algebras and BiHom-bialgebras . SIGMA Symmetry Integrability Geom. Methods Appl. 11(2015), 086. https://doi.org/10.3842/SIGMA.2015.086.Google Scholar
Guo, L., An introduction to Rota–Baxter algebra, Surveys of Modern Mathematics, 4, International Press, Somerville, MA; Higher Education Press, Beijing, 2012.Google Scholar
Hartwig, J. T., Larsson, D., and Silvestrov, S. D., Deformations of Lie algebras using 𝜎-derivations . J. Algebra 295(2006), 314–361. https://doi.org/10.1016/j.jalgebra.2005.07.036.Google Scholar
Joni, S. A. and Rota, G.-C., Coalgebras and bialgebras in combinatorics . Stud. Appl. Math. 61(1979), 93–139. https://doi.org/10.1002/sapm197961293.Google Scholar
Larsson, D. and Silvestrov, S. D., Quasi-hom-Lie algebras, central extensions and 2-cocycle-like identities . J. Algebra 288(2005), 321–344. https://doi.org/10.1016/j.jalgebra.2005.02.032.Google Scholar
Liu, L., Makhlouf, A., Menini, C., and Panaite, F., Rota–Baxter operators on BiHom-associative algebras and related structures. 2017. arxiv:1703.07275.Google Scholar
Liu, L., Makhlouf, A., Menini, C., and Panaite, F., BiHom-pre-Lie algebras, BiHom-Leibniz algebras and Rota–Baxter operators on BiHom-Lie algebras. 2017. arxiv:1706.00474.Google Scholar
Loday, J.-L., Dialgebras . In: Dialgebras and other operads, Lecture Notes in Mathematics, 1763, Springer, Berlin, 2001, pp. 7–66. https://doi.org/10.1007/3-540-45328-8_2.Google Scholar
Makhlouf, A., Hom-dendriform algebras and Rota–Baxter Hom-algebras . In: Operads and universal algebra, Nankai Ser. Pure Appl. Math. Theor. Phys., 9, World Sci. Publ., Hackensack, NJ, 2012, pp. 147–171. https://doi.org/10.1142/9789814365123_0008.Google Scholar
Makhlouf, A. and Silvestrov, S., Hom-algebra structures . J. Gen. Lie Theory Appl. 2(2008), 51–64. https://doi.org/10.4303/jglta/S070206.Google Scholar
Makhlouf, A. and Silvestrov, S., Hom-algebras and Hom-coalgebras . J. Algebra Appl. 9(2010), 553–589. https://doi.org/10.1142/S0219498810004117.Google Scholar
Makhlouf, A. and Yau, D., Rota–Baxter Hom-Lie-admissible algebras . Comm. Algebra 42(2014), 1231–1257. https://doi.org/10.1080/00927872.2012.737075.Google Scholar
Panaite, F. and Van Oystaeyen, F., Twisted algebras and Rota–Baxter type operators . J. Algebra Appl. 16(2017), no. 4, 1750079. https://doi.org/10.1142/S0219498817500797.Google Scholar
Voiculescu, D., The coalgebra of the free difference quotient in free probability . Internat. Math. Res. Notices 2000 no. 2, 79–106. https://doi.org/10.1155/S1073792800000064.Google Scholar
Yau, D., Infinitesimal Hom-bialgebras and Hom-Lie bialgebras. 2010. arxiv:1001.5000.Google Scholar
Yau, D., Hom-Novikov algebras . J. Phys. A. 44(2011), 085202. https://doi.org/10.1088/1751-8113/44/8/085202.Google Scholar