Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Muldoon, Martin E.
1995.
Electrostatics and zeros of Bessel functions.
Journal of Computational and Applied Mathematics,
Vol. 65,
Issue. 1-3,
p.
299.
Muldoon, Martin E.
1998.
Recent Progress in Inequalities.
p.
309.
Laforgia, Andrea
Muldoon, Martin E.
and
Siafarikas, Panayiotos D.
2003.
Árpád Elbert, 1939–2001: a memorial tribute.
Journal of Computational and Applied Mathematics,
Vol. 153,
Issue. 1-2,
p.
1.
Kerimov, M. K.
2016.
Studies on the zeros of Bessel functions and methods for their computation: 3. Some new works on monotonicity, convexity, and other properties.
Computational Mathematics and Mathematical Physics,
Vol. 56,
Issue. 12,
p.
1949.
Kerimov, M. K.
2018.
Studies on the Zeroes of Bessel Functions and Methods for Their Computation: IV. Inequalities, Estimates, Expansions, etc., for Zeros of Bessel Functions.
Computational Mathematics and Mathematical Physics,
Vol. 58,
Issue. 1,
p.
1.

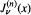 is unimodal on (
is unimodal on (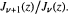 .
.