Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T17:08:22.399Z Has data issue: false hasContentIssue false
  • English
  • Français

Unimodular Roots of Special Littlewood Polynomials

Published online by Cambridge University Press:  20 November 2018

Idris David Mercer
Idris David Mercer*
Affiliation:
Department of Mathematics, Simon Fraser University, Burnaby, BC, V5A 1S6 e-mail: idmercer@math.sfu.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We call 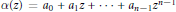$\alpha \left( z \right)={{a}_{0}}+{{a}_{1}}z+\cdot \cdot \cdot +{{a}_{n-1}}{{z}^{n-1}}$ a Littlewood polynomial if 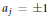${{a}_{j}}=\pm 1$ for all 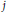$j$. We call 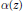$\alpha \left( z \right)$ self-reciprocal if 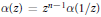$\alpha \left( z \right)={{z}^{n-1}}\alpha \left( 1/z \right)$, and call 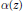$\alpha \left( z \right)$ skewsymmetric if 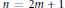$n=2m+1$ and 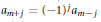${{a}_{m+j}}={{\left( -1 \right)}^{j}}{{a}_{m-j}}$ for all 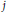$j$. It has been observed that Littlewood polynomials with particularly high minimum modulus on the unit circle in 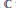$\mathbb{C}$ tend to be skewsymmetric. In this paper, we prove that a skewsymmetric Littlewood polynomial cannot have any zeros on the unit circle, as well as providing a new proof of the known result that a self-reciprocal Littlewood polynomial must have a zero on the unit circle.

Keywords

26C1030C1542A05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 49 , Issue 3 , 01 September 2006 , pp. 438 - 447
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Borwein, P. B., Computational Excursions in Analysis and Number Theory. CMS Books in Mathematics 10, Springer-Verlag, New York (2002).Google Scholar
[2] Erdélyi, T., On the zeros of polynomials with Littlewood-type coefficient constraints. Michigan Math. J. 49(2001), no. 1, 97–111.Google Scholar
[3] Erdőos, P., Some unsolved problems. Michigan Math. J. 4(1957), 291–300.Google Scholar
[4] Gilbert, A. D. and Smyth, C. J., Zero-mean cosine polynomials which are non-negative for as long as possible. J. London Math. Soc. (2) 62(2000), no. 2, 489–504.Google Scholar
[5] Konvalina, J. and Matache, V., Palindrome-polynomials with roots on the unit circle. C. R. Math. Rep. Acad. Sci. Canada 26(2004), no. 2, 39–44.Google Scholar
[6] Littlewood, J. E., On polynomials Σ n ±zm, Σ n eαmizm, z = eθi . J. London Math. Soc. 41(1966), 367–376.Google Scholar
[7] Littlewood, J. E., Some Problems in Real and Complex Analysis. D.C. Heath, Lexington, MA, 1968.Google Scholar
[8] Pólya, G. and Szegö, G., Problems and Theorems in Analysis. Volume II, Springer-Verlag, New York, 1976.Google Scholar
[9] Robinson, L., Polynomials with plus or minus one coefficients: growth properties on the unit circle. M.Sc. thesis, Simon Fraser University 1997.Google Scholar
[10] Spencer, J., Six standard deviations suffice. Trans. Amer.Math. Soc. 289(1985), no. 2, 679–706.Google Scholar