No CrossRef data available.
Article contents
Uniqueness of Almost Everywhere Convergent Vilenkin Series
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
D. J. Grubb [3] has shown that uniqueness holds, under a mild growth condition, for Vilenkin series which converge almost everywhere to zero. We show that, under even less restrictive growth conditions, one can replace the limit function 0 by an arbitrary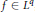 
$f\,\in \,{{L}^{q}}$, when 
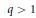$q\,>\,1$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2004
References
[1]
Bokaev, N. A. and Skvortsov, V. A., A generalization of a uniqueness theorem for series in multiplicative systems. Vestnik Moskov. Univ. Ser. I Mat. Mekh. 1987, 11–15.Google Scholar
[2]
Daly, J. E. and Phillips, K. L., A note on H1 multipliers for locally compact Vilenkin groups. Canad. Math. Bull. 41 (1998), 392–397.Google Scholar
[3]
Grubb, D. J., Sets of uniqueness in compact 0-dimensional metric groups Trans. Amer.Math. Soc. 301(1987) 239–249.Google Scholar
[4]
Vilenkin, N. Ya., On a class of complete orthonormal systems. Izv. Akad. Nauk. SSSR, Ser.Mat. 11 (1947), 363–400.Google Scholar
[5]
Wade, W. R., The bounded convergence theorem. Amer.Math. Monthly 81 (1974), 387–389.Google Scholar
You have
Access