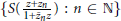Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ji Izuchi, Kei
2006.
Singular inner functions whose Frostman shifts are Carleson–Newman Blaschke products.
Complex Variables and Elliptic Equations,
Vol. 51,
Issue. 3,
p.
255.
Bayart, Frédéric
and
Gorkin, Pamela
2007.
How to get universal inner functions.
Mathematische Annalen,
Vol. 337,
Issue. 4,
p.
875.
Aron, Richard
and
Gorkin, Pamela
2007.
An Infinite Dimensional Vector Space of Universal Functions for H∞ of the Ball.
Canadian Mathematical Bulletin,
Vol. 50,
Issue. 2,
p.
172.
Bayart, Frédéric
Gorkin, Pamela
Grivaux, Sophie
and
Mortini, Raymond
2009.
Bounded universal functions for sequences of holomorphic self-maps of the disk.
Arkiv för Matematik,
Vol. 47,
Issue. 2,
p.
205.
Grosse-Erdmann, Karl-G.
and
Mortini, Raymond
2009.
Universal functions for composition operators with non-automorphic symbol.
Journal d'Analyse Mathématique,
Vol. 107,
Issue. 1,
p.
355.
Walmsley, David
2020.
Large vector spaces generated by bounded universal functions.
Journal of Mathematical Analysis and Applications,
Vol. 492,
Issue. 1,
p.
124393.