Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kuang, Yang
and
Feldstein, Alan
1990.
Monotonic and Oscillatory Solutions of a Linear Neutral Delay Equation with Infinite Lag.
SIAM Journal on Mathematical Analysis,
Vol. 21,
Issue. 6,
p.
1633.
Buhmann, Martin
and
Iserles, Arieh
1993.
Stability of the discretized pantograph differential equation.
Mathematics of Computation,
Vol. 60,
Issue. 202,
p.
575.
Iserles, Arieh
and
Liu, Yunkang
1994.
On Pantograph Integro-Differential Equations.
Journal of Integral Equations and Applications,
Vol. 6,
Issue. 2,
Derfel, Gregory
1995.
Operator Theory and Boundary Eigenvalue Problems.
p.
100.
Liu, Yunkang
1996.
Asymptotic behaviour of functional-differential equations with proportional time delays.
European Journal of Applied Mathematics,
Vol. 7,
Issue. 1,
p.
11.
Derfel, G.
and
Vogl, F.
1996.
On the asymptotics of solutions of a class of linear functional-differential equations.
European Journal of Applied Mathematics,
Vol. 7,
Issue. 5,
p.
511.
Iserles, Arieh
and
Liu, Yunkang
1997.
Integro-differential Equations and Generalized Hypergeometric Functions.
Journal of Mathematical Analysis and Applications,
Vol. 208,
Issue. 2,
p.
404.
Iserles, Arieh
and
Liu, Yunkang
1997.
On Neutral Functional–Differential Equations with Proportional Delays.
Journal of Mathematical Analysis and Applications,
Vol. 207,
Issue. 1,
p.
73.
Si, Jian-Guo
and
Cheng, Sui-Sun
2002.
ANALYTIC SOLUTIONS OF A FUNCTIONAL DIFFERENTIAL EQUATION WITH PROPORTIONAL DELAYS.
Bulletin of the Korean Mathematical Society,
Vol. 39,
Issue. 2,
p.
225.
Si, Jian-Guo
and
Wang, Xin-Ping
2002.
Analytic solutions of a second-order iterative functional differential equation.
Computers & Mathematics with Applications,
Vol. 43,
Issue. 1-2,
p.
81.
Si, Jianguo
Zhang, Weinian
and
Kim, Gwang-Hui
2004.
Analytic solutions of an iterative functional differential equation.
Applied Mathematics and Computation,
Vol. 150,
Issue. 3,
p.
647.


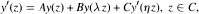
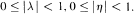 It is shown that y has exponential order equal to one if
It is shown that y has exponential order equal to one if 