No CrossRef data available.
Article contents
Vanishing of multizeta values over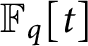 
$\mathbb {F}_q[t]$ at negative integers
Published online by Cambridge University Press: 18 January 2021
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let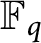 
$\mathbb {F}_q$
be the finite field of q elements. In this paper, we study the vanishing behavior of multizeta values over
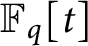$\mathbb {F}_q[t]$
at negative integers. These values are analogs of the classical multizeta values. At negative integers, they are series of products of power sums
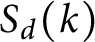$S_d(k)$
which are polynomials in t. By studying the t-valuation of
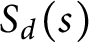$S_d(s)$
for
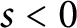$s < 0$
, we show that multizeta values at negative integers vanish only at trivial zeros. The proof is inspired by the idea of Sheats in the proof of a statement of “greedy element” by Carlitz.
Keywords
- Type
- Article
- Information
- Creative Commons
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.- Copyright
- © Canadian Mathematical Society 2021
References
Böckle, G.,
The distribution of the zeros of the Goss zeta-function for
$A={F}_2\left[x,y\right]/ \left({y}^2+y+{x}^3+x+1\right)$
. Math. Z. 275(2013), nos. 3–4, 835–861.10.1007/s00209-013-1162-9CrossRefGoogle Scholar
$A={F}_2\left[x,y\right]/ \left({y}^2+y+{x}^3+x+1\right)$
. Math. Z. 275(2013), nos. 3–4, 835–861.10.1007/s00209-013-1162-9CrossRefGoogle ScholarBroadhurst, D. J. and Kreimer, D.,
Association of multiple zeta values with positive knots via Feynman diagrams up to
$9$
loops
. Phys. Lett. B. 393(1997), nos. 3–4, 403–412.CrossRefGoogle Scholar
$9$
loops
. Phys. Lett. B. 393(1997), nos. 3–4, 403–412.CrossRefGoogle ScholarBurgos Gil, J. I. and Fresán, J., Multiple zeta values: from numbers to motives, to appear in Clay Mathematics Proceedings. http://javier.fresan.perso.math.cnrs.fr/mzv.pdf.Google Scholar
Carlitz, L., Finite sums and interpolation formulas over
$GF\left[{p}^n,x\right]$
. Duke Math. J. 15(1948), 1001–1012.CrossRefGoogle Scholar
$GF\left[{p}^n,x\right]$
. Duke Math. J. 15(1948), 1001–1012.CrossRefGoogle ScholarChang, C.-Y., On characteristic p multizeta values, Algebraic number theory and related topics 2012
. RIMS Kôkyûroku Bessatsu, B51, Research Institute For Mathematical Sciences, Kyoto, 2014, pp. 177–202.Google Scholar
Deligne, P. and Goncharov, A. B.,
Groupes fondamentaux motiviques de Tate mixte
. Ann. Sci. École Norm. Sup. 38(2005), no. 1, 1–56, Series 4.CrossRefGoogle Scholar
Diaz-Vargas, J.,
Riemann hypothesis for
${F}_p\left[T\right]$
. J. Number Theory 59(1996), no. 2, 313–318.CrossRefGoogle Scholar
${F}_p\left[T\right]$
. J. Number Theory 59(1996), no. 2, 313–318.CrossRefGoogle ScholarEuler, L.,
Meditationes circa singulare serierum genus
. Novi Comm. Acad. Sci. Petropol. 20(1775), 140–186, Reprinted in “Opera Omnia”, ser. 1, vol. 15, B. G. Teubner, Berlin, 1927, pp. 217–267.Google Scholar
Furusho, H., Komori, Y., Matsumoto, K., and Tsumura, H.,
Desingularization of complex multiple zeta-functions
. Amer. J. Math. 139(2017), no. 1, 147–173.10.1353/ajm.2017.0002CrossRefGoogle Scholar
Goncharov, A. B., Multiple ζ-values, Galois groups, and geometry of modular varieties
. In: European Congress of Mathematics, Vol. I (Barcelona, 2000), Progr. Math., 201, Birkhäuser, Basel, 2001, pp. 361–392.Google Scholar
Goncharov, A. B.,
Galois symmetries of fundamental groupoids and noncommutative geometry
. Duke Math. J. 128(2005), no. 2, 209–284.CrossRefGoogle Scholar
Goss, D.,
$v$
-Adic zeta functions,
$L$
-series and measures for function fields
. Invent. Math. 55(1979), 107–119.10.1007/BF01390084CrossRefGoogle Scholar
$v$
-Adic zeta functions,
$L$
-series and measures for function fields
. Invent. Math. 55(1979), 107–119.10.1007/BF01390084CrossRefGoogle ScholarGoss, D., Basic structures of function field arithmetic. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 35, Springer-Verlag, Berlin, 1996.CrossRefGoogle Scholar
Hoffman, M. E.,
Multiple harmonic series
. Pacific J. Math. 152(1992), no. 2, 275–290.10.2140/pjm.1992.152.275CrossRefGoogle Scholar
Masri, R.,
Multiple zeta values over global function fields
. In: Multiple Dirichlet series, automorphic forms, and analytic number theory, Proc. Sympos. Pure Math., 75, American Mathematical Society, Providence, RI, 2006, pp. 157–175.Google Scholar
Sheats, J. T.,
The Riemann hypothesis for the Goss zeta function for
${\textbf{F}}_q\left[T\right]$
. J. Number Theory 71(1998), no. 1, 121–157.10.1006/jnth.1998.2232CrossRefGoogle Scholar
${\textbf{F}}_q\left[T\right]$
. J. Number Theory 71(1998), no. 1, 121–157.10.1006/jnth.1998.2232CrossRefGoogle ScholarThakur, D. S., Function field arithmetic. World Scientific Publishing,
River Edge, NJ, 2004.CrossRefGoogle Scholar
Thakur, D. S.,
Power sums with applications to multizeta and zeta zero distribution for
${F}_q\left[t\right]$
. Finite Fields Appl. 15(2009), no. 4, 534–552.10.1016/j.ffa.2009.04.002CrossRefGoogle Scholar
${F}_q\left[t\right]$
. Finite Fields Appl. 15(2009), no. 4, 534–552.10.1016/j.ffa.2009.04.002CrossRefGoogle ScholarThakur, D. S.,
Multizeta values for function fields: a survey
. J. Théor. Nombres Bordeaux 29(2017), no. 3, 997–1023.CrossRefGoogle Scholar
Zagier, D., Values of zeta functions and their applications. In: First European Congress of Mathematics, Vol. II (Paris, 1992), Progr. Math., 120, Birkhäuser, Basel, 1994, pp. 497–512.Google Scholar
You have
Access
Open access