Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T14:37:58.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Vector Fields and the Cohomology Ring of Toric Varieties

Published online by Cambridge University Press:  20 November 2018

Kiumars Kaveh
Kiumars Kaveh*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, B.C. e-mail: kaveh@math.ubc.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 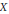$X$ be a smooth complex projective variety with a holomorphic vector field with isolated zero set 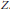$Z$. From the results of Carrell and Lieberman there exists a filtration 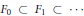${{F}_{0}}\subset {{F}_{1}}\subset \cdot \cdot \cdot$ of 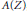$A\left( Z \right)$, the ring of $\mathbb{C}$-valued functions on 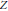$Z$, such that 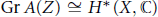$\text{Gr }A\left( Z \right)\cong {{H}^{*}}\left( X,\mathbb{C} \right)$ as graded algebras. In this note, for a smooth projective toric variety and a vector field generated by the action of a 1-parameter subgroup of the torus, we work out this filtration. Our main result is an explicit connection between this filtration and the polytope algebra of 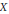$X$.

Keywords

14M2552B20Toric varietytorus actioncohomology ringsimple polytopepolytope algebra
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 3 , 01 September 2005 , pp. 414 - 427
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] M., M. Brion, The structure of the polytope algebra. Tohoku Math. J. (2) 49(1997), 1–32.Google Scholar
[2] Carrell, J. B., Torus Actions and Cohomology. In: Algebraic Quotients. Torus Actions and Cohomology. The Adjoint Representation and The Adjoint Action, Encyclopaedia Math. Sci. 131, Springer, Berlin, 2002, pp. 83–158,.Google Scholar
[3] Carrell, J. B. and Lieberman, D. I., Holomorphic vector fields and Kähler manifolds. Inven. Math. 21(1973), 303–309.Google Scholar
[4] Carrell, J. B. and Lieberman, D. I., Vector fields and Chern numbers. Math. Ann. 225(1977), 263–273.Google Scholar
[5] Fulton, W., Introduction to toric varieties. Annals of Mathematics Studies 131, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[6] Khovanskiĭ, A. G., Hyperplane sections of polyhedra, toric varieties and discrete groups in Lobachevskiĭ space. Funktsional. Anal. i Prilozhen. 20(1986), 50–61. 96.Google Scholar
[7] McMullen, P., The polytope algebra. Adv. Math. 78(1989), 76–130.Google Scholar
[8] Oda, T., Geometry of toric varieties. In: Proceedings of the Hyderabad Conference on Algebraic Groups, Manoj Prakashan, Madras, 1991, pp. 407–440.Google Scholar
[9] Pukhlikov, A. V. and Khovanskiĭ, A. G., The Riemann-Roch theorem for integrals and sums of quasipolynomials on virtual polytopes. (Russian) Algebra i Analiz 4(1992), 188–216. translation in St. Petersburg Math. J. 4(1993), 789–81.Google Scholar
[10] Puppe, V., Deformation of algebras and cohomology of fixed point sets. Manuscripta Mathematica 30(1979), 119–136.Google Scholar
[11] Timorin, V. A., An analogue of the Hodge-Riemann relations for simple convex polyhedra. (Russian) Uspekhi Mat. Nauk 54(1999), 113–162. translation in Russian Math. Surveys 54(1999), 381–426.Google Scholar