Article contents
The Weakly Nilpotent Graph of a Commutative Ring
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $R$ be a commutative ring with non-zero identity. In this paper, we introduce the weakly nilpotent graph of a commutative ring. The weakly nilpotent graph of
$R$ be a commutative ring with non-zero identity. In this paper, we introduce the weakly nilpotent graph of a commutative ring. The weakly nilpotent graph of  $R$ denoted by
$R$ denoted by 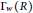 ${{\Gamma }_{w}}(R)$ is a graph with the vertex set
${{\Gamma }_{w}}(R)$ is a graph with the vertex set 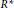 ${{R}^{\star }}$ and two vertices
${{R}^{\star }}$ and two vertices  $x$ and
$x$ and  $y$ are adjacent if and only if
$y$ are adjacent if and only if 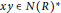 $x\,y\in N{{(R)}^{\star }}$, where
$x\,y\in N{{(R)}^{\star }}$, where 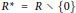 ${{R}^{\star }}=R\backslash \{0\}$ and
${{R}^{\star }}=R\backslash \{0\}$ and 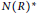 $N{{(R)}^{\star }}$ is the set of all non-zero nilpotent elements of
$N{{(R)}^{\star }}$ is the set of all non-zero nilpotent elements of  $R$. In this article, we determine the diameter of weakly nilpotent graph of an Artinian ring. We prove that if
$R$. In this article, we determine the diameter of weakly nilpotent graph of an Artinian ring. We prove that if 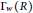 ${{\Gamma }_{w}}(R)$ is a forest, then
${{\Gamma }_{w}}(R)$ is a forest, then 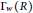 ${{\Gamma }_{w}}(R)$ is a union of a star and some isolated vertices. We study the clique number, the chromatic number, and the independence number of
${{\Gamma }_{w}}(R)$ is a union of a star and some isolated vertices. We study the clique number, the chromatic number, and the independence number of 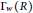 ${{\Gamma }_{w}}(R)$. Among other results, we show that for an Artinian ring
${{\Gamma }_{w}}(R)$. Among other results, we show that for an Artinian ring  $R$,
$R$, 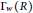 ${{\Gamma }_{w}}(R)$ is not a disjoint union of cycles or a unicyclic graph. For Artinan rings, we determine diam
${{\Gamma }_{w}}(R)$ is not a disjoint union of cycles or a unicyclic graph. For Artinan rings, we determine diam 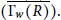 $\overline{({{\Gamma }_{w}}(R))}$. Finally, we characterize all commutative rings
$\overline{({{\Gamma }_{w}}(R))}$. Finally, we characterize all commutative rings  $R$ for which
$R$ for which 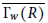 $\overline{({{\Gamma }_{w}}(R))}$ is a cycle, where
$\overline{({{\Gamma }_{w}}(R))}$ is a cycle, where 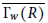 $\overline{({{\Gamma }_{w}}(R))}$ is the complement of the weakly nilpotent graph of
$\overline{({{\Gamma }_{w}}(R))}$ is the complement of the weakly nilpotent graph of  $R$.
$R$.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2017
References
- 3
- Cited by


