Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T08:57:19.601Z Has data issue: false hasContentIssue false
  • English
  • Français

Weakly separated Bessel systems of model spaces

Part of: Function theory on the disc Special classes of linear operators

Published online by Cambridge University Press:  04 October 2021

Alberto Dayan Open the ORCID record for Alberto Dayan [Opens in a new window]
Alberto Dayan*
Affiliation:
Department of Mathematics, Washington University in St. Louis, One Brookings Drive, St. Louis, MO63130, USA
*
e-mail: alberto.dayan@wustl.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that any weakly separated Bessel system of model spaces in the Hardy space on the unit disc is a Riesz system and we highlight some applications to interpolating sequences of matrices. This will be done without using the recent solution of the Feichtinger conjecture, whose natural generalization to multidimensional model subspaces of 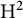${\mathrm {H}}^2$ turns out to be false.

Keywords

Inner functions of one complex variableBlaschke productsLinear operators in reproducing-kernelHilbert spaces

MSC classification

Primary: 30J05: Inner functions
Secondary: 30J10: Blaschke products 47B32: Operators in reproducing-kernel Hilbert spaces (including de Branges, de Branges-Rovnyak, and other structured spaces)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 3 , September 2022 , pp. 723 - 742
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was partially supported by National Science Foundation Grant DMS 1565243.

References

Agler, J. and Mc Carthy, J. E., Pick interpolation and Hilbert function spaces, Graduate Studies in Mathematics, 44, American Mathematical Society, Providence, RI, 2002.CrossRefGoogle Scholar
Aleman, A., Hartz, M., Mc Carthy, J. E., and Richter, S., Interpolating sequences in spaces with the Pick property . Int. Math. Res. Not. IMRN 2019(2019), no. 12, 3832–3854.CrossRefGoogle Scholar
Carleson, L., An interpolation problem for bounded analytic functions . Am. J. Math. 80(1958), no. 4, 921–930.CrossRefGoogle Scholar
Carleson, L., Interpolation by bounded analytic functions and the Corona problem . Ann. Math. 76(1962), no. 3, 547–559.CrossRefGoogle Scholar
Casazza, P. G., Christensen, O., Lindner, A. M., and Verhsynin, R., Frames and the Feichtinger conjecture . Proc. Am. Math. Soc. 133(2005), no. 4, 1025–1033.10.1090/S0002-9939-04-07594-XCrossRefGoogle Scholar
Dayan, A., Interpolating matrices . Integ. Equat. Oper. Theory 92(2020), 49 .CrossRefGoogle Scholar
Garcia, R. S., Mashreghi, J., and Ross, W. T., Introduction to model spaces and their operators, Cambridge Studies in Advanced Mathematics, 148, Cambridge University Press, Cambridge, 2016.CrossRefGoogle Scholar
Garnett, J. B., Bounded analytic functions, Revised 1st ed., Graduate Texts in Mathematics, 236, Springer, New York, 2007.Google Scholar
Marcus, A. W., Spielman, D. A., and Srivastava, N., Interlacing families II: Mixed characteristic polynomials and the Kadison-Singer problem. Ann. Math. 182(2015), no. 1, 327–350.CrossRefGoogle Scholar
Nikol’skiĭ, N. K., Treatise on the shift operator: Spectral function theory, Springer Series in Soviet Mathematics, Springer, New York, 1985.Google Scholar
Nikol’skiĭ, N. K., Operators, functions and systems: An easy reading . In: Model operators and systems. Vol. 2, Mathematical Surveys and Monographs, 93, American Mathematical Society, Providence, RI, 2002.Google Scholar
Shapiro, H. S. and Shields, A. L., On some interpolation problems for analytic functions . Amer. J. Math. 83(1961), 513–532.CrossRefGoogle Scholar
Weaver, N., The Kadison-Singer problem in discrepancy theory . Discrete Math. 278(2004), 227–239.CrossRefGoogle Scholar