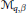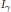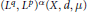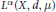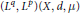Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Feuto, Justin
2013.
INTRINSIC SQUARE FUNCTIONS ON FUNCTIONS SPACES INCLUDING WEIGHTED MORREY SPACES.
Bulletin of the Korean Mathematical Society,
Vol. 50,
Issue. 6,
p.
1923.
Liu, Feng
Wu, Huoxiong
and
Zhang, Daiqing
2014.
On the Multilinear Singular Integrals and Commutators in the Weighted Amalgam Spaces.
Journal of Function Spaces,
Vol. 2014,
Issue. ,
p.
1.
Fofana, Ibrahim
Faléa, Falé Roland
and
Kpata, Bérenger Akon
2015.
A class of subspaces of Morrey spaces and norm inequalities on Riesz potential operators.
Afrika Matematika,
Vol. 26,
Issue. 5-6,
p.
717.
Auscher, Pascal
and
Prisuelos-Arribas, Cruz
2017.
Tent space boundedness via extrapolation.
Mathematische Zeitschrift,
Vol. 286,
Issue. 3-4,
p.
1575.
Adama, Aïssata
Feuto, Justin
and
Fofana, Ibrahim
2019.
A weighted inequality for potential type operators.
Advances in Pure and Applied Mathematics,
Vol. 10,
Issue. 4,
p.
413.
Wang, Hua
2020.
Estimates for Fractional Integral Operators and Linear Commutators on Certain Weighted Amalgam Spaces.
Journal of Function Spaces,
Vol. 2020,
Issue. ,
p.
1.
Diarra, Nouffou
and
Fofana, Ibrahim
2021.
On preduals and Köthe duals of some subspaces of Morrey spaces.
Journal of Mathematical Analysis and Applications,
Vol. 496,
Issue. 2,
p.
124842.
Jia, Hongchao
Tao, Jin
Yang, Dachun
Yuan, Wen
and
Zhang, Yangyang
2022.
Special John-Nirenberg-Campanato spaces via congruent cubes.
Science China Mathematics,
Vol. 65,
Issue. 2,
p.
359.
Zhao, Yirui
Sawano, Yoshihiro
Tao, Jin
Yang, Dachun
and
Yuan, Wen
2023.
Bourgain–Morrey Spaces Mixed with Structure of Besov Spaces.
Proceedings of the Steklov Institute of Mathematics,
Vol. 323,
Issue. 1,
p.
244.
Zhao, Yirui
Sawano, Yoshihiro
Tao, Jin
Yang, Dachun
and
Yuan, Wen
2023.
Пространства типа Бургейна-Морри со структурой пространств Бесова.
Труды Математического института имени В. А. Стеклова,
Vol. 323,
Issue. ,
p.
252.