Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T13:13:19.725Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero-divisor Graphs of Ore Extensions Over Reversible Rings

Published online by Cambridge University Press:  20 November 2018

E. Hashemi  and
R. Amirjan
E. Hashemi
Affiliation:
Department of Mathematics, Shahrood University of Technology,, P.O. Box: 316h-999561, Shahrood, Iran e-mail: eb_hashemi@yahoo.com
R. Amirjan
Affiliation:
Department of Mathematics, Shahrood University of Technology,, P.O. Box: 316h-999561, Shahrood, Iran e-mail: eb_hashemi@yahoo.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $R$ be an associative ring with identity. First we prove some results about zero-divisor graphs of reversible rings. Then we study the zero-divisors of the skew power series ring 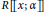$R\left[\!\left[ x;\,\alpha \right]\!\right]$, whenever $R$ is reversible $\alpha$-compatible. 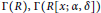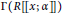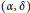Moreover, we compare the diameter and girth of the zero-divisor graphs of $\Gamma \left( R \right),\,\Gamma \left( R[x;\,\alpha ,\,\delta ] \right)$, and $\Gamma \left( R\left[\!\left[ x;\,\alpha \right]\!\right] \right)$, when $R$ is reversible and $\left( \alpha ,\,\delta \right)$-compatible.

Keywords

13B2505C1216S36zero-divisor graphsreversible ringsMcCoy ringspolynomial ringspower series rings
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 4 , 01 December 2016 , pp. 794 - 805
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Afkhami, M., Khashayarmanesh, K., and Khorsandi, M. R., Zero-divisor graphs of Ore extension rings. J. Algebra Appl. 10(2011), no. 6,1309-1317. http://dx.doi.Org/10.1142/S0219498811005191 Google Scholar
[2] Akbari, S. and Mohammadian, A., Zero-divisor graphs of non-commutative rings. J. Algebra 296(2006), no. 2, 462–479. http://dx.doi.Org/10.1016/j.jalgebra.2005.07.007 Google Scholar
[3] Anderson, D. D. and Camillo, V., Semigroups and rings whose zero products commute. Comm. Algebra 27(1999), no. 6, 2847–2852. http://dx.doi.Org/10.1080/00927879908826596 Google Scholar
[4] Anderson, D. E and Livingston, P. S., The zero-divisor graph of a commutative ring. J. Algebra 217(1999), no. 2, 434–447. http://dx.doi.Org/10.1006/jabr.1998.7840 Google Scholar
[5] Anderson, D. E and Mulay, S. B., On the diameter and girth of a zero-divisor graph. J. Pure Appl. Algebra 210(2007), no. 2, 543–550. http://dx.doi.Org/10.1016/j.jpaa.2006.10.007 Google Scholar
[6] Anderson, D. D. and Naseer, M., Beck's coloring of a commutative ring. J. Algebra 159(1993), no. 2, 500–514. http://dx.doi.Org/10.1006/jabr.1993.1171 Google Scholar
[7] Armendariz, E. P., Koo, H. K., and Park, J. K., Isomorphic Ore extensions. Comm. Algebra 15(1987), no. 12, 2633–2652. http://dx.doi.Org/10.1080/00927878708823556 Google Scholar
[8] Axtel, M., Coykendall, J., and Stickles, J., Zero-divisor graphs of polynomials and power series over commutative rings. Comm. Algebra 33(2005), no. 6, 2043–2050. http://dx.doi.Org/10.1081/ACB-200063357 Google Scholar
[9] Beck, I., Coloring of commutative rings. J. Algebra 116(1988), no. 1, 208–226. http://dx.doi.Org/10.1016/0021-8693(88)90202-5 Google Scholar
[10] Bell, H. E., Near-rings in which each element is a power of itself. Bull. Austral. Math. Soc. 2(1970), 363–368. http://dx.doi.Org/10.1017/S0004972700042052 Google Scholar
[11] Cohn, P. M., Reversible rings. Bull. London Math. Soc. 31(1999), no. 6, 641–648. http://dx.doi.Org/10.1112/SOO24609399006116 Google Scholar
[12] Fields, D. E., Zero divisors and nilpotent elements in power series rings. Proc. Amer. Math. Soc. 27(1971), 427–433. http://dx.doi.Org/10.1O9O/SOOO2-9939-1971-0271100-6 Google Scholar
[13] Hashemi, E., On ideals which have the weakly insertion of factors property. J. Sci. Islam. Repub. Iran 19(2008), no. 2,145-152,190.Google Scholar
[14] Hashemi, E., Polynomial extensions of quasi-Baer rings. Acta Math. Hungar. 107(2005), no. 3, 207–224. http://dx.doi.Org/10.1007/s10474-005-0191-1 Google Scholar
[15] Hirano, Y., On the uniqueness of rings of coefficients in skew polynomial rings. Publ. Math. Debrecen 54(1999), no. 3-4, 489–495.Google Scholar
[16] Hong, C. Y., Kim, N. K., and Kwak, T. K., Ore extensions ofBaer and p.p.-rings. J. Pure Appl. Algebra 151(2000), no. 3, 215–226. http://dx.doi.Org/10.1 01 6/S0022-4049(99)00020-1 Google Scholar
[17] Kaplansky, I., Commutative rings. Revised ed., University of Chicago Press, Chicago, 111.-London, 1974.Google Scholar
[18] Kim, N. K. and Lee, Y., Extensions of reversible rings. J. Pure Appl. Algebra 185(2003), no. 1-3, 207–223. http://dx.doi.Org/10.1016/S0022-4049(03)00109-9 Google Scholar
[19] Krempa, J., Some examples of reduced rings. Algebra Colloq. 3(1996), no. 4, 289–300.Google Scholar
[20] Krempa, J. and Niewieczerzal, D., Rings in which annihilators are ideals and their application to semigroup rings. Bull. Acad. Polon. Sci. Ser. Math. Astronom. Phys. 25(1977), no. 9, 851–856.Google Scholar
[21] Lam, T. Y., A first course in noncommutative rings. Graduate Text in Mathematics, 131, Springer-Verlag, New York, 1991. http://dx.doi.Org/10.1007/978-1 -4684-0406-7 Google Scholar
[22] Lambek, J., On the representation of modules by sheaves of factor modules. Canad. Math. Bull. 14(1971), 359–368. http://dx.doi.Org/10.4153/CMB-1971-065-1 Google Scholar
[23] Lucas, T., The diameter of a zero divisor graph. J. Algebra 301(2006), no. 1,174-193. http://dx.doi.Org/10.1016/j.jalgebra.2006.01.019 Google Scholar
[24] McCoy, N. H., Annihilators in polynomial rings. Amer. Math. Monthly 64(1957), 28–29. http://dx.doi.Org/10.2307/2309082 Google Scholar
[25] Nielsen, P. P., Semi-commutativity and the McCoy condition. J. Algebra 298(2006), no. 1,134-141. http://dx.doi.Org/10.1016/j.jalgebra.2OO5.10.008 Google Scholar
[26] Redmond, S. P., The zero-divisor graph of a non-commutative ring. In: Commutative rings, Nova Sci. Publ., Hauppauge, NY, 2002, pp. 39–47.Google Scholar
[27] Shin, G., Prime ideals and sheaf representation ofapseudo symmetric rings. Trans. Amer. Math. Soc. 184(1973), 43–60. http://dx.doi.Org/10.1090/S0002-9947-1973-0338058-9 Google Scholar
[28] Wright, S. E., Lengths of paths and cycles in zero-divisor graphs and digraphs of semigroups. Comm. Algebra 35(2007), no. 6, 1987–1991. http://dx.doi.Org/!0.1080/00927870701247146 Google Scholar