Porson's Law Extended

L. P. E. Paker

doi:10.1017/S0009838800003335

Porson's Law Extended

Published online by Cambridge University Press: 11 February 2009

L. P. E. Paker

Show author details

L. P. E. Paker: Affiliation:
University of Newcastle upon Tyne

Article contents

Extract
References

Get access

Rights & Permissions

Extract

Paul Maas extended the law still further: ‘The following rule applies to several metres which contain the rhythm 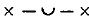: no word can end after a long anceps, except at the caesura in the middle of the line.’ He lists the types of metre to which the rule applies as the stichic iambic trimeters and trochaic tetrameters of the early iambographers and the Attic tragedians, the dactylo-epitrites of Bacchylides, the trochaic trimeters and dimeters of Alcman's Partheneion, the end (but not the beginning) of the iambic tetrameters of Sophocles' Ichneutae, and ‘certain rare metres, whose conformity to this rule may be due to accident’

Type: Research Article
Information: The Classical Quarterly , Volume 16 , Issue 1 , May 1966 , pp. 1 - 26

DOI: https://doi.org/10.1017/S0009838800003335 [Opens in a new window]
Copyright: Copyright © The Classical Association 1966

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

^{page 1 note 1} Porson, R., supplement to the preface to Euripidis Hecuba (Cambridge, 1802).Google Scholar

^{page 1 note 2} Havet, L. and Duvau, L., Cours élémentaire de métrique grecque et latine, 4th ed. (Paris, 1896).Google Scholar

^{page 1 note 3} Griechische Metrik in Gercke-Norden, , Einleitung in die Altertumswissenschaft, Bd. I (Leipzig, 1927), § 48Google Scholar; Greek Metre trans. Lloyd-Jones, H. (Oxford, 1962), p. 34.Google Scholar

^{page 1 note 4} Strictly, word of more than one syllable (Porson: ‘hypermonosyllabon‘).

^{page 1 note 5} Abriss der griechischen Verslehre (Munich, 1949) § 36.Google Scholar

^{page 1 note 6} ‘Porsons Gesetz‘, Kgl. böhm. Gesellsch. 1909, ix (Prague, 1910).Google Scholar

^{page 1 note 7} ‘Porsons Gesetz‘, Hermes xlix (1914), 229–45.Google Scholar

^{page 1 note 8} Griechische Metrik, 3rd ed. (Göttingen, 1962), p. 6.Google Scholar

^{page 1 note 9} ‘Lois et règies dans le trimètre iambique et le tetrametre trochaique’, R.É.G. ixxii (1959). 67–80.Google Scholar

^{page 2 note 1} Op. cit., p. 6, n. I.

^{page 3 note 1} I hope to publish a more detailed study of this development.

^{page 3 note 2} On caesura in pendent (or trailing) rhythm in verses with blunt end and vice-versa see my article, ‘Some recent Researches on the Versification of Pindar and Bacchylides‘, B.I.C.S. v (1958), 13–24.Google Scholar

^{page 4 note 1} It is interesting to note that Bacchylides (in the second ‘colon‘ of the third verse of the strophe of poem 3) has word-end at this point in thirteen out of fourteen sapphic hendecasyllables, while the remaining verse, 22, has the alternative horatian caesura Detween shorts.

^{page 4 note 2} See Metre, § 48, p. 34 and ‘Kolometrie in den Daktyloepitriten des Bakchylides’, Philologus lxiii (1904), 297–309.Google Scholar

^{page 5 note 1} ‘Dactylo-epitrites in Bacchylides‘, Hermes Ixxxiv (1956), 248–53.Google Scholar

^{page 5 note 2} Recherches sur les mètres de la lyrique chorale grecque. La structure du vers (Paris, 1953).Google Scholar The conclusions which Irigoin draws from his observations are not valid. See review by Dover, K. J. (J.H.S. lxxii [1954])Google Scholar and my article, B.I.C.S. v (1958).Google Scholar

^{page 7 note 1} The above information, with differences of detail and of arrangement, is contained in Barrett's article.

^{page 7 note 2} This statement is, of course, intended to apply only to dactylo-epitrites. I am in debted to Professor K. J. Dover for drawing my attention to 3 str. 1, a catalectic iambic trimeter with penthemimeral caesura in twelve out of thirteen repetitions: In eight of these verses the caesura is preceded by short anceps. This evidence that Bacchylides had no objection to … outside dactylo-epitrites lends support to my view that its absence in them is attributable to the general rarity of short anceps itself, rather than to an inhibition about word-end after it.

^{page 10 note 1} It is still more unlike lyric iambics.

^{page 10 note 2} A comparison of my figures for dochmiacs with those published by Conomis, N. C. (‘The Dochmiacs of Greek Drama‘, Henna xcii [1964], 23–50)Google Scholar shows some slight divergences. For example, his figures for the three most common types of dochmiac are: 233. Scansion must be to some extent a matter of opinion, so that it is unlikely that any two metricians working independently would produce identical figures.

^{page 11 note 1} For the few, dubious examples, see Conomis, op. cit.

^{page 11 note 2} Accepting Wilamowitz's . Wecklein, by inserting after the first , makes the verse nto three cretics.

^{page 12 note 1} Porson and Havet, op. cit.; also Maas, , Metre § 48Google Scholar and Bill, F. X., Beiträge zur Lex Porsoniana (Emsdetten, 1932).Google Scholar

^{page 13 note 1} See White, J. W., The Verse of Greek Comedy, p. 65.Google Scholar

^{page 13 note 2} See also Maas, , Metre, § 48.Google Scholar

^{page 13 note 3} There are seven violations in the trimeters of Cyc.: 120 and 672 with , 304 and 639 with elision, 210 (), 681 () and 682 (); and one in the Ichneutae, 269 (Cf. Cyc. 682).

^{page 16 note 1} G. W. Bond ad loc. analyses 103–4 as 3 doch. He follows Wilamowitz in taking as a syncopated doch., which I find hard to accept.

^{page 16 note 2} Miss A. M. Dale regards 836 as ‘a pendent version of 833–4‘ () is hard to analyse, but we have no business to reject anything in Greek metre simply because we cannot put a name to it.

^{page 17 note 1} Greek Particles, p. 502 (e).

^{page 17 note 2} Marginalia Scaenica, pp. 22 ff.

^{page 17 note 3} ‘Notes on Sophocles' Antigone‘, C.Q..N. S. vii (1957). 12–27.Google Scholar

^{page 17 note 4} was actually supplied by Hermann. He also, however, added a second to fill the verse out to the length of 834.

^{page 18 note 1} Miss A. M. Dale, to whom I am indebted for some most valuable criticism and suggestions, proposes the following solution: 834

850

This could be analysed mol. mol. (= cr. cr.) sp. Cretic , molossus , and spondee , could all be produced by syncopation from the iambic metron. Miss Dale offers as a possible parallel for the responsion Trach. 846 = 858 . However, in dealing with a passage as individual in rhythm as this the finding of parallels is not of die first importance. Miss Dale's emendation conforms with the main metrical prerequisite here, suitability to the context.

^{page 18 note 2} See, for example, Kraus, W., Strophen-gestaltung in der griechischen Tragödie. I. Aischylos und Sophokles, p. 69.Google Scholar

^{page 22 note 1} At 129 the manuscript reading produces word-end at the bucolic bridge. O. Müller's should be accepted, as it is by Fraenkel. The alteration is trifling and the gain in metrical elegance and intelligibility immense.

^{page 24 note 1} Irigoin's explanation, however, leaves the problem of why monosyllables should be exempt from Porson's law.

^{page 25 note 1} See above, p. 16.

^{page 25 note 2} So Badham. LP. It seems unlikely that the corruption here could affect the incidence of word-end at the end of the colon.

Article contents

Porson's Law Extended

Extract

Access options

References

Save article to Kindle

Save article to Dropbox

Save article to Google Drive

Reply to: Submit a response

Your details

You have entered the maximum number of contributors

Conflicting interests