Experimental study on the influence of preliminary desiccation on the swelling pressure and hydraulic conductivity of compacted bentonite

Abstract

In deep geological repositories, compacted bentonites have been proposed for use as barrier materials for isolating nuclear waste. The prevailing thermo-hydro-mechanical boundary conditions in the repositories may affect the swelling capacity and permeability of the compacted bentonites. In this study, the effect of preliminary desiccation on the subsequent hydro-mechanical behaviour (swelling pressure and hydraulic conductivity) of compacted Calcigel bentonite was investigated experimentally at 22°C and 80°C. In the first stage of the test, the compacted specimens were subjected to suction-controlled desiccation at 22°C and 80°C using the vapour-equilibrium technique. After the water content reached equilibrium at a given suction, the axial, radial and volumetric shrinkage strains were measured. Afterwards, constant-volume swelling-pressure tests were performed on the desiccated specimens (second test stage) by saturating the dried specimens with deionized water at 22°C and 80°C. At the end of the swelling-pressure test, the hydraulic conductivities of four saturated specimens were measured at each temperature. The volumetric shrinkage strain of the compacted bentonite during desiccation is controlled by suction instead of temperature. In addition, the preliminary desiccation increases both the swelling pressure and hydraulic conductivity of compacted bentonite, particularly if compacted bentonite undergoes extreme desiccation at an applied suction of >700 MPa.

Compacted bentonite is one of the candidate buffer-clay materials for the deep geological disposal of high-level radioactive wastes (HLWs) (e.g. Pusch, 1980b; Bucher & Müller, 1989; Komine & Ogata, 1996; Delage et al., 1998; Lloret et al., 2003; Schanz & Tripathy, 2009; Ye et al., 2009; Yigzaw et al., 2016). Because of its high swelling ability and low permeability, the compacted bentonite buffer is suitable for safely isolating HLWs from the biosphere.

Compacted bentonite blocks, initially unsaturated, are installed in a disposal hole of a disposal tunnel (Fig. 1). In the disposal hole, the compacted bentonite blocks are placed in the gap between the cold host rock and the hot canister containing HLWs. Sealing the disposal hole is generally initiated after installation of all buffer components and canisters (Johannesson et al., 2014). Before sealing the disposal hole, a buffer protection made of a plastic or of rubber is installed in the technical gap between the host rock and buffer blocks. This protection prevents the buffer blocks from adsorbing water from the wet host rock before initiating the backfilling work. Through the duration of protection (~3 months), the bentonite buffer blocks are usually under a thermal gradient.

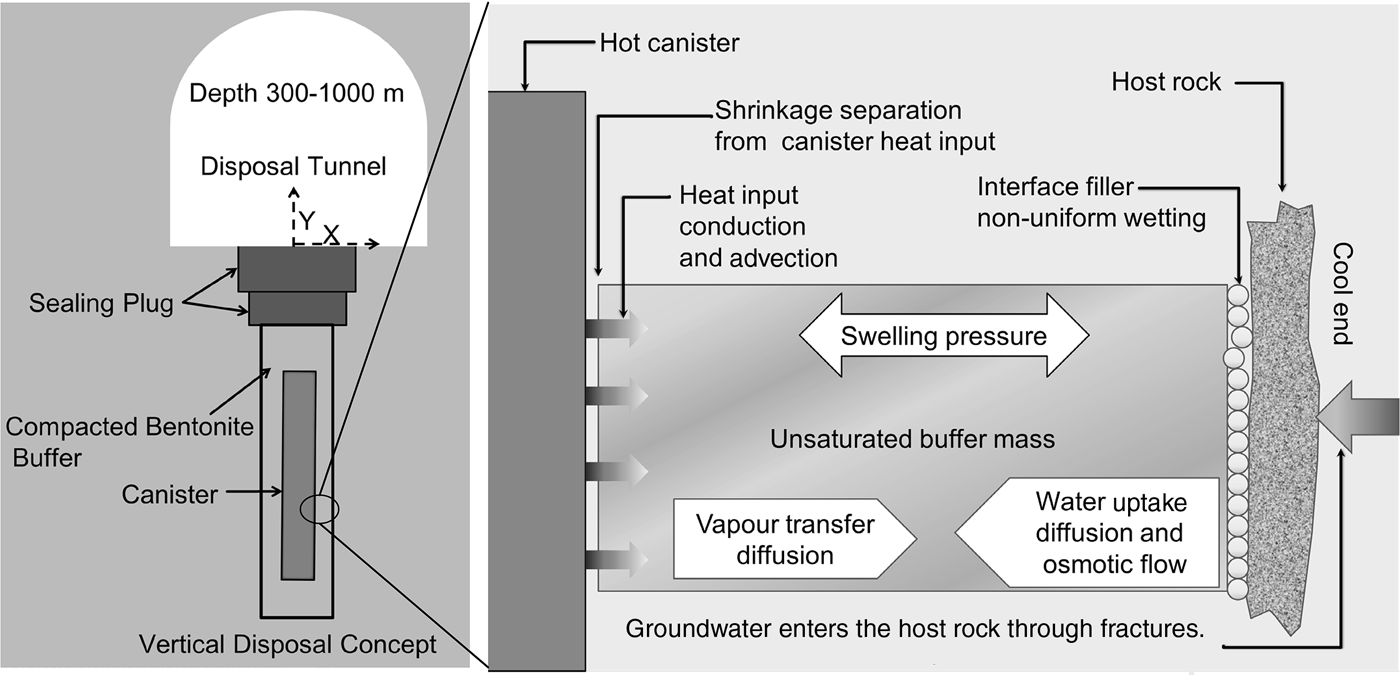
Fig. 1. Schematic view of the deep geological disposal of HLWs (modified after Pusch & Yong, 2006).

The hydro-mechanical behaviour of compacted bentonite-based materials under a thermal gradient has been studied using column tests, mock-ups and full-scale tests (e.g. Åkesson et al., 2009; Johannesson et al., 2014; Villar et al., 2016; Tripathy et al., 2017). With increasing distance between the measuring sites and the heater that simulates the hot canister, the water content of the measuring sites increases, whereas the bulk density decreases. Also, under a thermal gradient, water in the unsaturated bentonite-based materials migrates from high temperatures (hot zones) to low temperatures (cold zones). This water migration finally results in dehydration and shrinkage of the bentonite buffer close to the high-temperature zone. Preliminary desiccation due to this thermal gradient may further affect the swelling ability and permeability of the bentonite buffer close to the high-temperature zone.

Previous studies have addressed the influence of preliminary desiccation on the subsequent swelling behaviour and permeability of clays in cyclical wetting–drying experiments (e.g. Osipov et al., 1987; Day, 1994; Al-Homoud et al., 1995; Alonso et al., 1999; Albrecht & Benson, 2001; Akcanca & Aytekin, 2014). However, studies of the influence of preliminary desiccation at elevated temperatures (i.e. 80°C) on the subsequent swelling behaviour and permeability of compacted bentonite have not been undertaken. Previous studies using cyclical wetting–drying tests suggest that desiccation will significantly increase the hydraulic conductivity of the compacted clays. Conclusions about this swelling behaviour are not unequivocal, however, because both increases and decreases in the swelling ability of clays have been reported to result from preliminary desiccation.

The objective of this study was to evaluate the effect of preliminary desiccation on the swelling pressure and hydraulic conductivity of a compacted Ca,Mg-rich bentonite. Specimens with a similar compaction dry density first underwent suction-controlled desiccation at 22°C and 80°C. The change in water content of each specimen was monitored during the desiccation by periodically recording the weight of the specimen. Equilibrium in the water content is generally assumed when the weight of a specimen remains unchanged. Subsequently, constant-volume swelling-pressure tests were performed on the specimens. The specimens dried at 22°C and 80°C were saturated with deionized water at 22°C and 80°C, respectively. After the swelling pressure reached equilibrium, the hydraulic conductivities of four saturated specimens were measured at the respective temperatures.

MATERIALS

The material used in this study was Calcigel bentonite, from Bavaria, Germany, purchased from Süd-Chemie AG Moosburg, Germany, which has been considered to be one of the potential buffer and backfilling materials in the German multi-barrier concept for disposing of HLWs (Xie et al., 2012). The mineralogical composition and main properties of the bentonite are listed in Table 1 and Table 2, respectively. The mineralogical composition provided by Süd-Chemie AG Moosburg, Germany, was similar to that reported in the literature (Madsen, 1998; Agus, 2005; Schanz & Tripathy, 2009; Baille, 2014). The total specific surface area, measured by the ethylene glycol monoethyl ether (EGME) method (Cerato & Lutenegger, 2002), was 436 m²/g. The total cation exchange capacity was 74 cmol(+)/kg and the exchangeable cations were Na⁺ (2 cmol(+)/kg), Ca²⁺ (27 cmol(+)/kg) and Mg²⁺ (19 cmol(+)/kg) (Baille, 2014). The liquid limit, plastic limit and shrinkage limit were 119%, 45% and 10%, respectively. The <2 µm clay fraction was 54% and the particle specific gravity was 2.80.

Table 1. Mineralogical composition.

Table 2. Material properties.

EXPERIMENTAL METHODS

Preparation of the compacted specimens

An adequate amount of water was mixed with the bentonite powder (particle size <0.1 mm) in ambient laboratory conditions and the sample was kept in a sealed bucket for 2 weeks to allow for water content equilibrium. Subsequently, the water content and total suction of the prepared bentonite were measured by drying at 105°C and with a chilled-mirror hygrometer (AquaLab-3TE, Meter Group), respectively. The remaining material was used to produce the compacted specimens by statically compacting the bentonite in a stainless-steel sample ring (50.0–50.5 mm inner diameter and 20.0 mm height) to a target height of 15.2 mm. The initial compaction dry density (named ‘dry density after compaction’ in Table 3) varied slightly from 1.56 to 1.59 mg/m³. For all of the compacted bentonite specimens, the initial water content and total suction values were 20.0% and 14 MPa, respectively.

Table 3. Overview of the testing programme with applied temperatures and suctions, dry densities at various test stages, and swelling pressures and hydraulic conductivities in the saturated state.

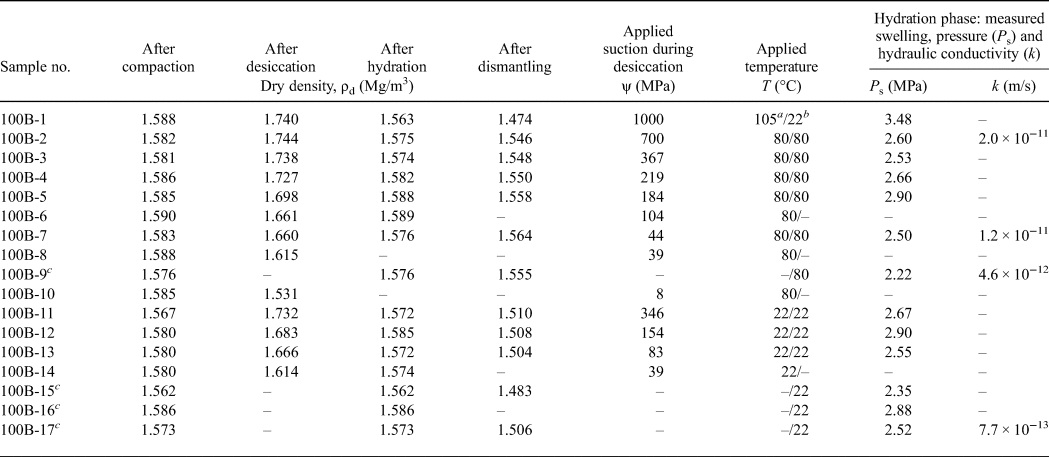
^a Value refers to the applied temperature during the desiccation phase.

^b Value refers to the temperature during the hydration phase.

^c Reference sample without undergoing preliminary desiccation phase.

Suction-controlled desiccation tests at 22°C and 80°C

The drying tests were carried out using the water-vapour technique. A schematic diagram of the drying test setup used is shown in Fig. 2. The drying phase was applied to all of the specimens except specimens 100B-9, 100B-15, 100B-16 and 100B-17, which were used as reference specimens and thus did not undergo preliminary desiccation.

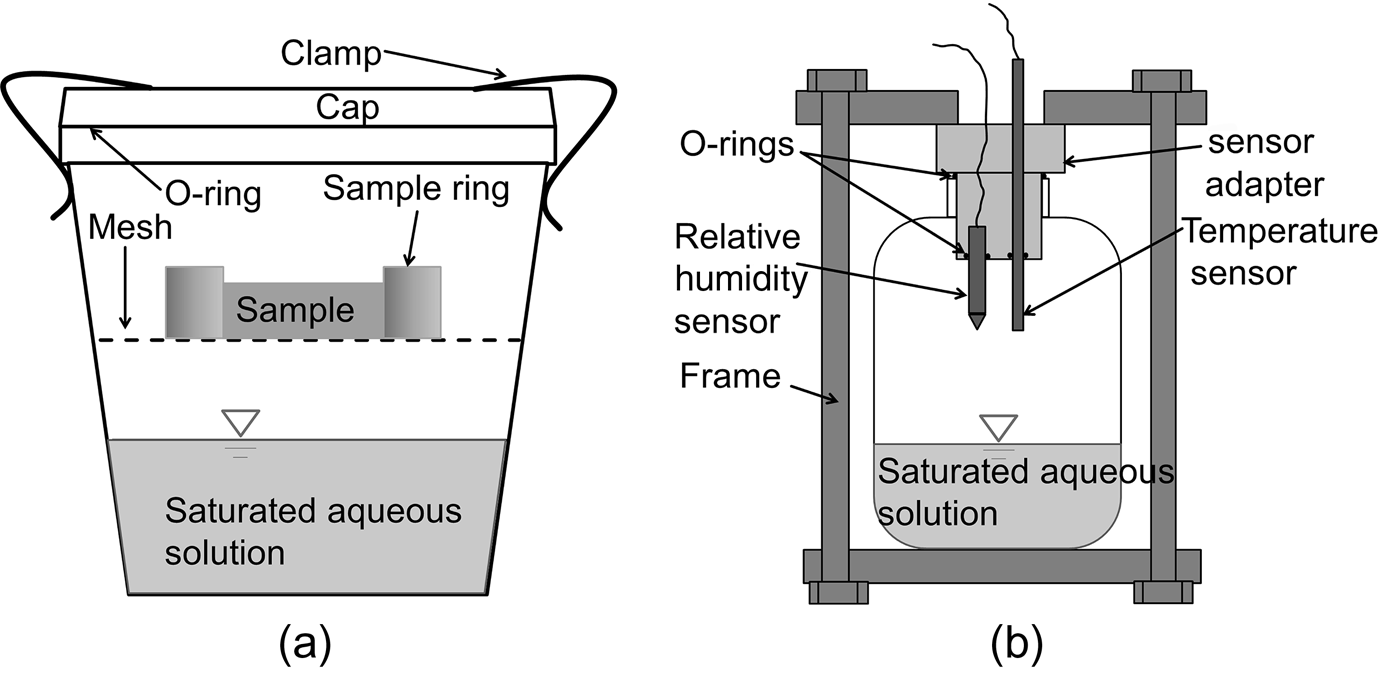
Fig. 2. Schematic diagram of: (a) suction-control device; and (b) device for measuring the suction of saturated aqueous solutions.

A compacted specimen with a sample ring was placed on a plastic mesh that was fixed in the middle of a desiccator (Fig. 2a). The saturated salt solution at the bottom of a sealed desiccator provided a constant relative humidity (RH) at a given temperature. Various RH conditions were applied by using various aqueous solutions at the respective controlled temperatures. The saturated solutions used in this study are presented in Table 4. The temperatures during the tests were controlled by placing the desiccator in an oven at 80±0.1°C or in a constant temperature-controlled room at 22±0.1°C. For a given saturated aqueous solution at temperatures of 22°C and 80°C, the corresponding suction values were determined separately using the device shown in Fig. 2b. The device consists of a tightly closed container with a provision to insert two sensors for RH and temperature measurements. The sensors used in the present study were VAISALA HMP337, which consists of a humidity sensor based on the correlation of humidity to dielectric characteristics (capacitive-type RH sensor), and a thermocouple for temperature measurement. The RHs measured at the two temperatures of 22°C and 80°C were in agreement with those that have been reported in the literature (Greenspan, 1977; Delage et al., 1998; Tang & Cui, 2005). According to the RHs and temperatures measured in this study, the applied total suction (ψ) was calculated using equation 1 (Fredlund et al., 2012):

(1)$${\rm \psi} = -\displaystyle{{\hbox{R}T_K} \over {{\rm \nu}_{w0}{\rm \omega}_\nu}} \; \ln (RH)$$

where R is the universal (molar) gas constant (i.e. 8.31432 J/[mol K]); T _K is the absolute temperature 273.15 + T (K), T = temperature (°C); ν_ω0 is the specific volume of water or the inverse of the density of water (m³/kg); ω_ν is the molecular mass of water vapour (i.e. 18.016 kg/kmol); and RH is the measured relative humidity.

Table 4. Measured equilibrium suction, ψ (MPa), of the saturated solutions used at 22°C and 80°C.

The applied suction values during the drying tests for each specimen are listed in Table 3. In addition, it was assumed that the dry state of a specimen after oven drying at a temperature of 105°C corresponds to a suction of 1000 MPa (Fredlund et al., 2012). An oven with a temperature of 80°C provided suction of 700 MPa (Table 3), which was determined by RH and temperature measurements in the oven atmosphere. During the drying tests, the mass change of each specimen was determined periodically by removing it from the container and weighing it on a balance with a readability of 0.001 g. Once the mass of the specimens reached equilibrium (variation of specimen mass <0.001 g), the diameter and height of each specimen were measured using a calliper, and the dry density values were also calculated (referred to here as ‘dry density after desiccation’ in Table 3).

Swelling-pressure and hydraulic-conductivity tests

After the drying tests were terminated, all of the dried specimens except specimens 100B-6, 100B-8, 100B-10 and 100B-14 (Table 3) were transferred into an isochoric swelling-pressure device as shown in Fig. 3 (Romero, 1999; Schanz & Tripathy, 2009). Prior to use, the deformation of the isochoric swelling-pressure device and the load-cell measurement were calibrated with respect to the non-isothermal test conditions. Details of the calibration were given by Arifin (2008). The swelling-pressure tests were performed as one-step tests by supplying deionized water at the respective temperatures used in the preliminary desiccation phase.

Fig. 3. Experimental setup for the swelling-pressure and hydraulic-conductivity tests.

Due to the preliminary desiccation, all of the specimens except 100B-10 and the reference specimens experienced volumetric shrinkage, leading to increases in dry density (Table 3). Consequently, these specimens had diameters of <50 mm (inner diameter of the sample ring) and heights of <15.2 mm. The height of 15.2 mm corresponded to the net space height of the sample ring when the isochoric swelling-pressure device was assembled. The net space height of the sample ring was 15.2 mm because the height of the piston and upper porous disk was 4.8 mm. Because small initial radial and vertical gaps existed at the start of the hydration phase, the initial phase of hydration corresponded to the free-swelling condition. Hydration of the desiccated specimens under constant-volume conditions occurred until the initial radial and vertical gaps were filled with swollen bentonite particles.

The hydraulic conductivities of four saturated specimens (i.e. 100B-17, 100B-2, 100B-7 and 100B-9) were measured at the end of the hydration phase at the respective temperatures. Specimen 100B-17 was tested at 22°C and specimens 100B-2, 100B-7 and 100B-9 were tested at 80°C. The experimental setup is shown in Fig. 3. A constant water-pressure head of 24 kPa was applied by a volume–pressure controller at the bottom of specimen and the outflow at top of the specimen was measured using a burette. When the flows reached steady state, the saturated coefficient of hydraulic conductivity was calculated according to Darcy's law (Yong & Warkentin, 1975). The duration of each hydraulic conductivity test was ~45 days.

At the end of the hydration test, the swelling-pressure device was dismantled and the final dry densities of most of the specimens were determined by measuring their height and diameter. The height and diameter measurements show that the preliminary volumetric shrinkage was fully recovered in the desiccated specimens. The final dry densities were 0.8–5.7% smaller than the dry densities after hydration (Table 3). This is attributed to the slight deformation of the swelling-pressure device during the swelling-pressure test and the expansion of the specimen after releasing the swelling pressure. Because the times taken to dismantle the swelling pressure device and the subsequent measuring of specimen dimensions were not the same for each test, any errors due to these factors cannot be quantified. Therefore, the dry density after saturation was used as the relevant dry density to which the respective measured swelling pressure and hydraulic conductivity referred. The dry density after saturation was determined according to the water content and mass of a specimen before hydration and its volume after saturation under constant-volume conditions. The volume of a saturated specimen was determined based on the diameter of the sample ring (50.0–50.5 mm) and the net space height of the sample ring (15.2 mm).

RESULTS AND DISCUSSION

Relationships between preliminary desiccation, equilibrium water content and suction-water content

The evolution of water content with time at various applied suctions is presented in Fig. 4a for the drying tests at 22°C and in Fig. 4b for the drying tests at 80°C. The equilibrium water contents of all of the specimens except for 100B-10 were less than the initial water content of 20%, as the applied suctions were greater than the initial suction of 14 MPa. The equilibrium water content (i.e. 20.7%) at an applied suction of 8 MPa of specimen 100B-10 was slightly greater than the initial water content. This implies that the suction corresponding to the water content of 20% at 80°C was >8 MPa but <14 MPa, because the suction of compacted bentonite at a given water content decreased with increasing temperature (Villar et al., 2010).

Fig. 4. Evolution of the water content of compacted bentonite with elapsed time during suction-controlled desiccation at (a) 22°C and (b) 80°C (sample numbers and applied suctions are given in the key).

A comparison of the suction-water content relationships at 22°C and 80°C is shown in Fig. 5. For a given applied suction, the water content was slightly smaller for the specimens subjected to 80°C than for the specimens subjected to 22°C. In addition, for a given water content, the bentonite suction was smaller at the higher temperature. This implies that, once a thermal gradient is applied to the bentonite buffer with homogeneous initial water content, the suction of the buffer zone close to the heating source decreases, and thus a hydraulic gradient arises. This hydraulic gradient due to the thermal gradient in turn induces water movement from the low-suction region to the high-suction region of the buffer zone.

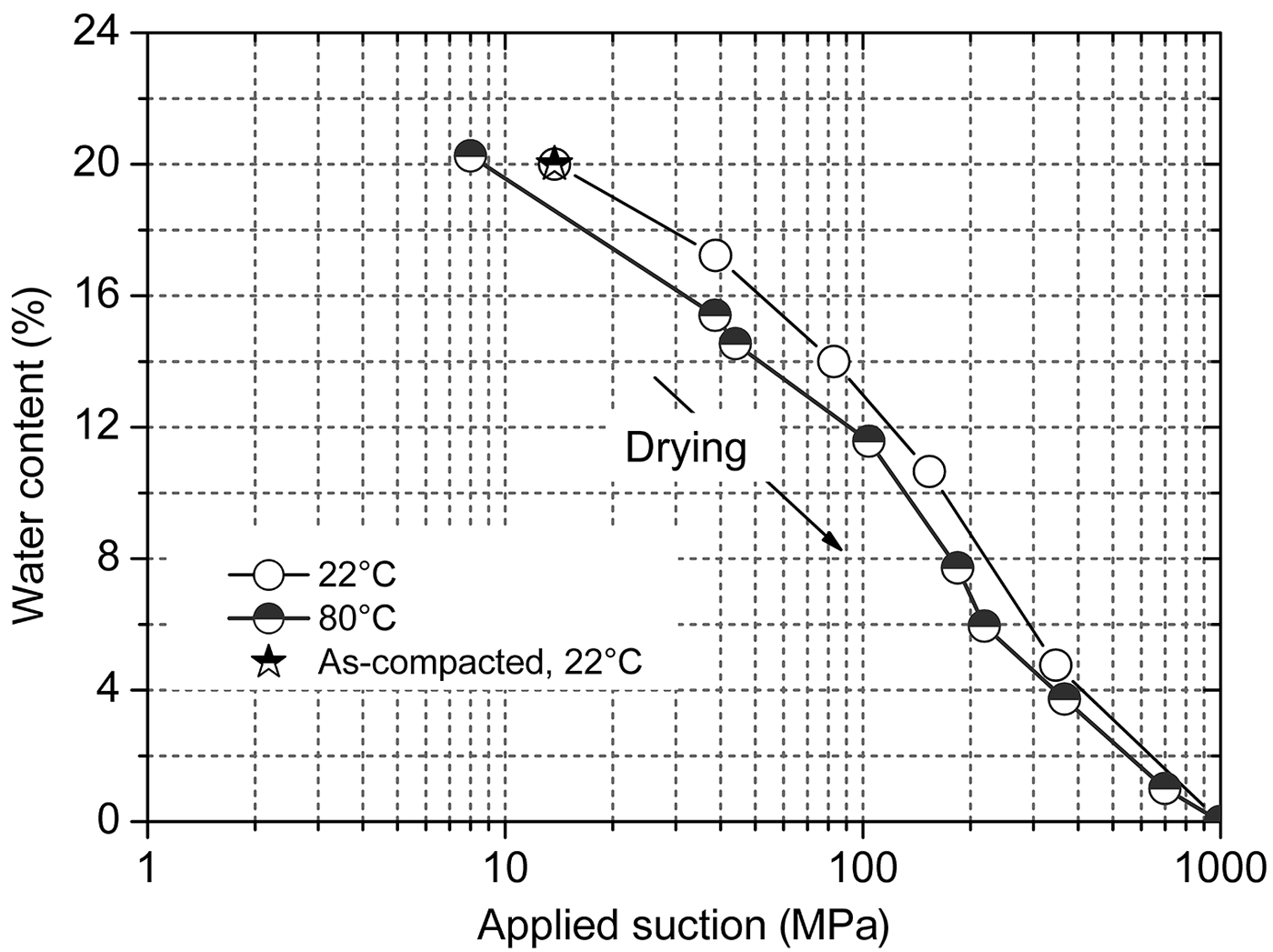
Fig. 5. Applied suction vs. water content of compacted bentonite at 22°C and 80°C.

Preliminary desiccation: shrinkage strains

The measured axial, radial and volumetric strains against the applied suction for both temperatures are presented in Fig. 6a,b,c, respectively. From the initial state corresponding to 14 MPa suction and zero strain, the axial, radial and volumetric strains increased linearly with increasing suction up to ~400 MPa for both temperatures. Beyond the suction range of 400 MPa, a further suction increase did not induce further strain. The suction of 400 MPa corresponds to RHs of 5.2% at 22°C and of 8.5% at 80°C. In these conditions, montmorillonites dominated by divalent exchangeable cations (e.g. Ca, Mg) experience transition from mono-hydrated- to dehydrated-layer water states (Mooney et al., 1952; Ferrage et al., 2007; Morodome & Kawamura, 2009). The removal of single-hydrated layer water probably does not affect macroscopic volume deformation. Consequently, the volumetric shrinkage strain is almost constant for suctions >400 MPa.

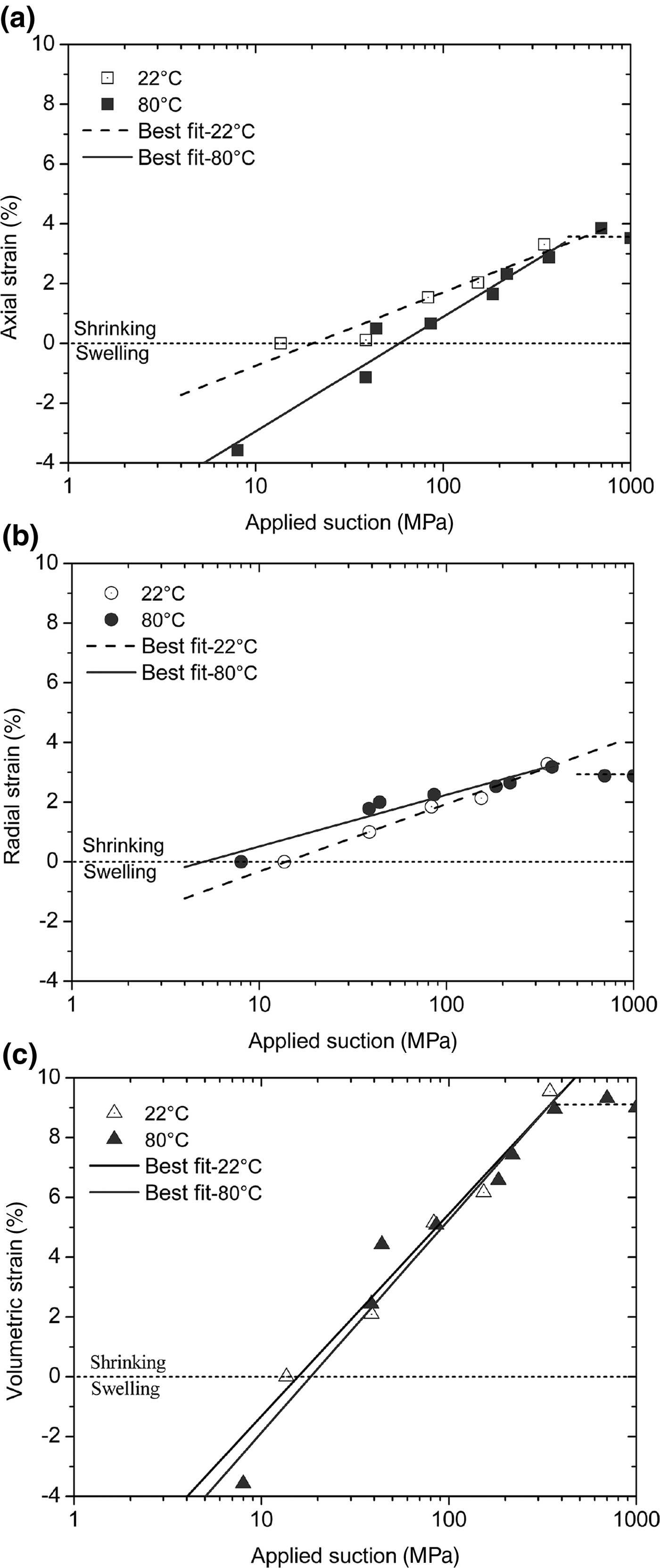
Fig. 6. Applied suction vs. (a) axial, (b) radial and (c) volumetric strains of compacted bentonite at 22°C and 80°C.

Moreover, the axial strain at a given suction was greater at 22°C than at 80°C (Fig. 6a), whereas the radial strain at a given suction followed the opposite trend (Fig. 6b). Consequently, the effect of temperature on the volumetric strain (Fig. 6c) was minor. The volumetric shrinkage strain of compacted bentonite during desiccation is controlled by suction or hydraulic gradients rather than by applied temperature or thermal gradients (Fig. 6).

Hydration phase: swelling pressure

The evolution of swelling pressure with elapsed time is presented in Fig. 7a for the tests at 22°C and in Fig. 7b for the tests at 80°C. The equilibrium swelling pressure was established more rapidly at the hydration temperature of 80°C. The swelling-pressure equilibrium time for the specimens tested at 22°C was ~300 h, whereas the swelling-pressure equilibrium time for specimens hydrated at 80°C was ~100 h. In addition, for a given temperature, dry density and water content before hydration had almost no influence on the swelling-pressure equilibrium time, but did affect the magnitude of the equilibrium swelling pressure.

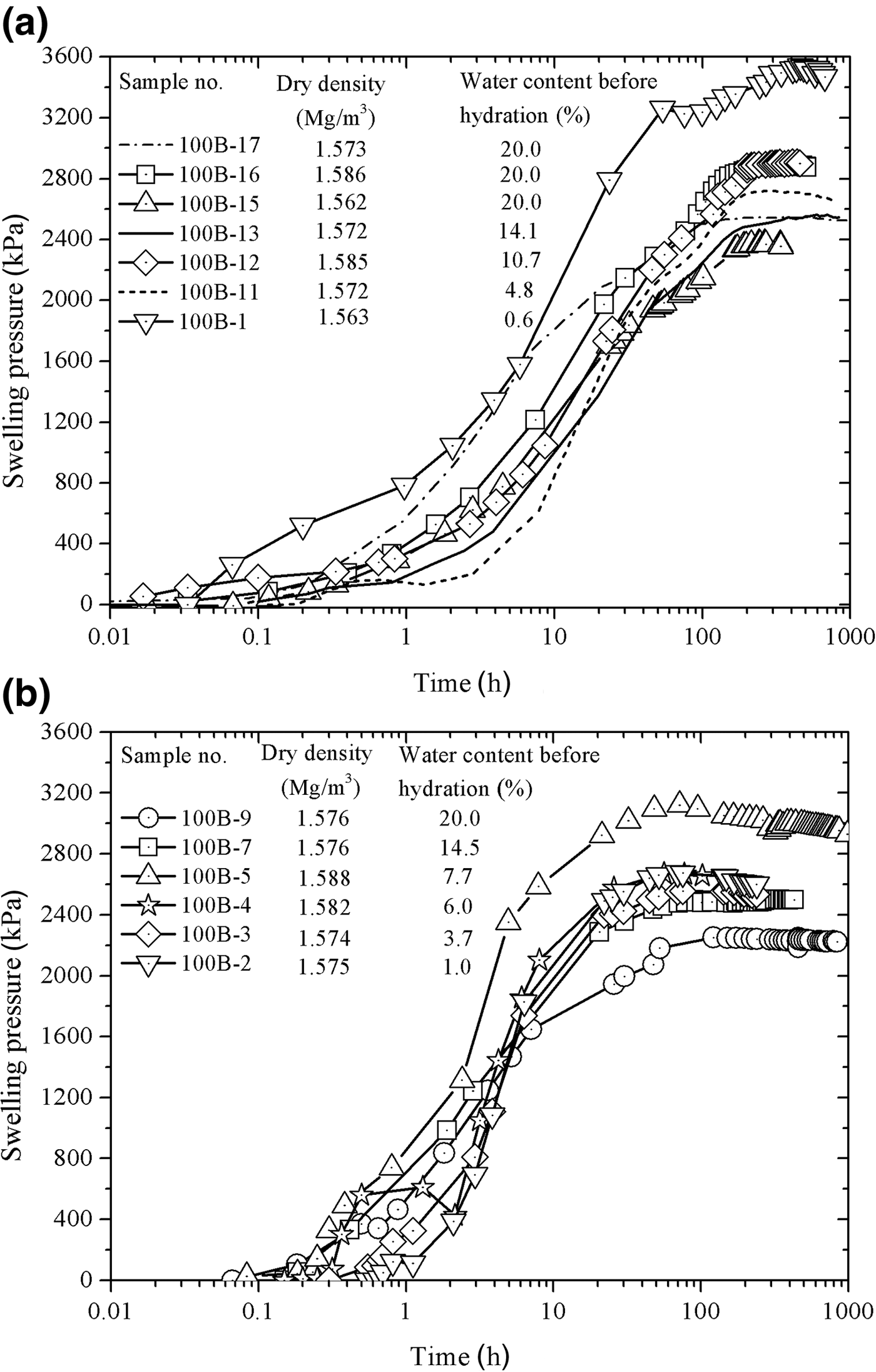
Fig. 7. Evolution of the swelling pressure of compacted bentonite with elapsed time in the case of saturating at (a) 22°C and (b) 80°C.

Figure 8 presents the equilibrium swelling pressure as a function of the dry density of the saturated specimens. The data in the literature (Schanz & Tripathy, 2009; Baille et al., 2010) were obtained from constant-volume swelling-pressure tests performed at 20°C on compacted Calcigel bentonite with mineralogical composition and material properties similar to the bentonite used in this study. The swelling pressures in this study were in reasonable agreement with the data from the literature (Fig. 8). In addition, temperature did not affect the swelling pressure–dry density relationship. For a given dry density, the swelling pressures at 80°C were slightly lower than those measured at 22°C (Fig. 9).

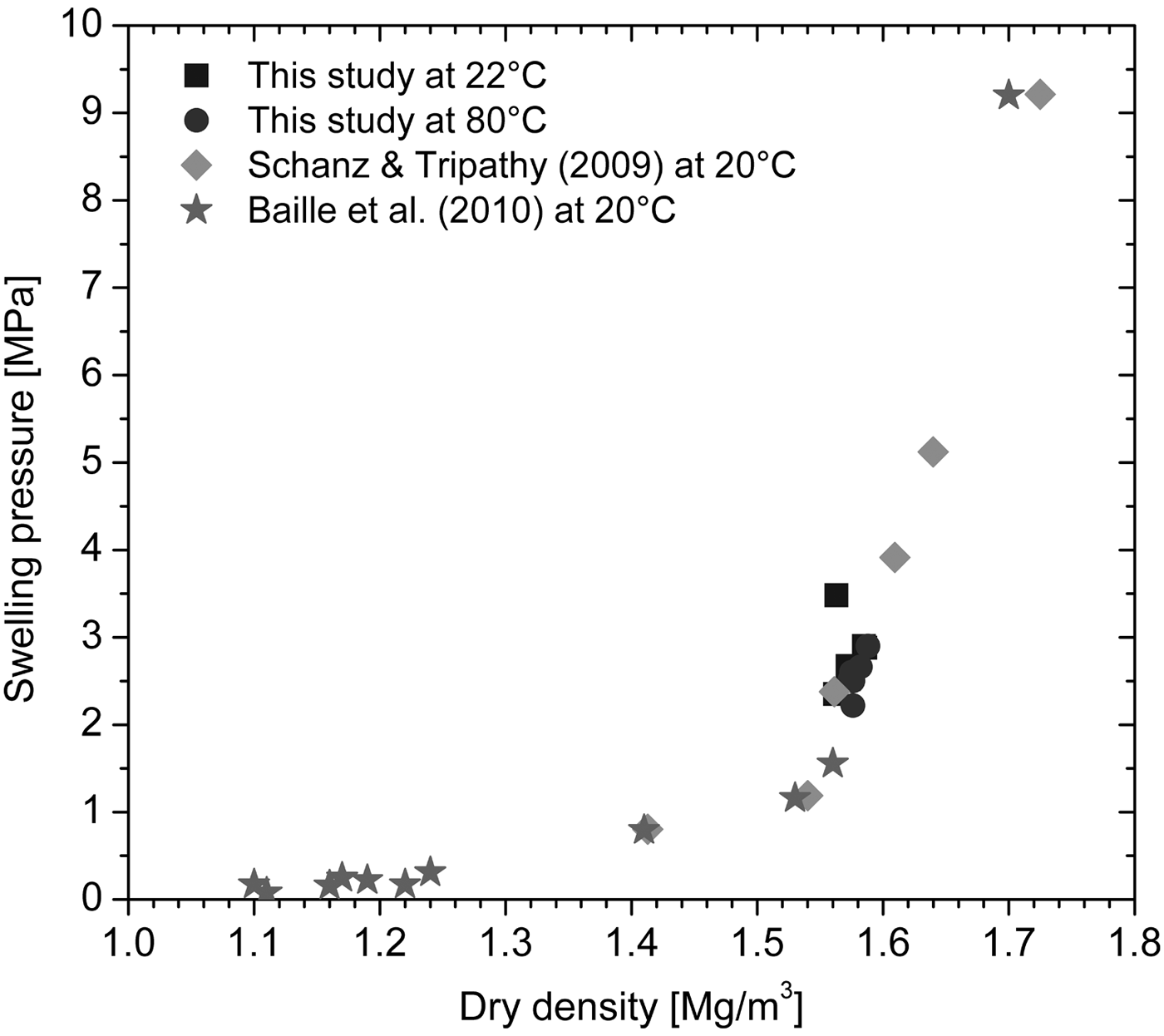
Fig. 8. Dependence of the swelling pressure of compacted bentonite on dry density after hydration.

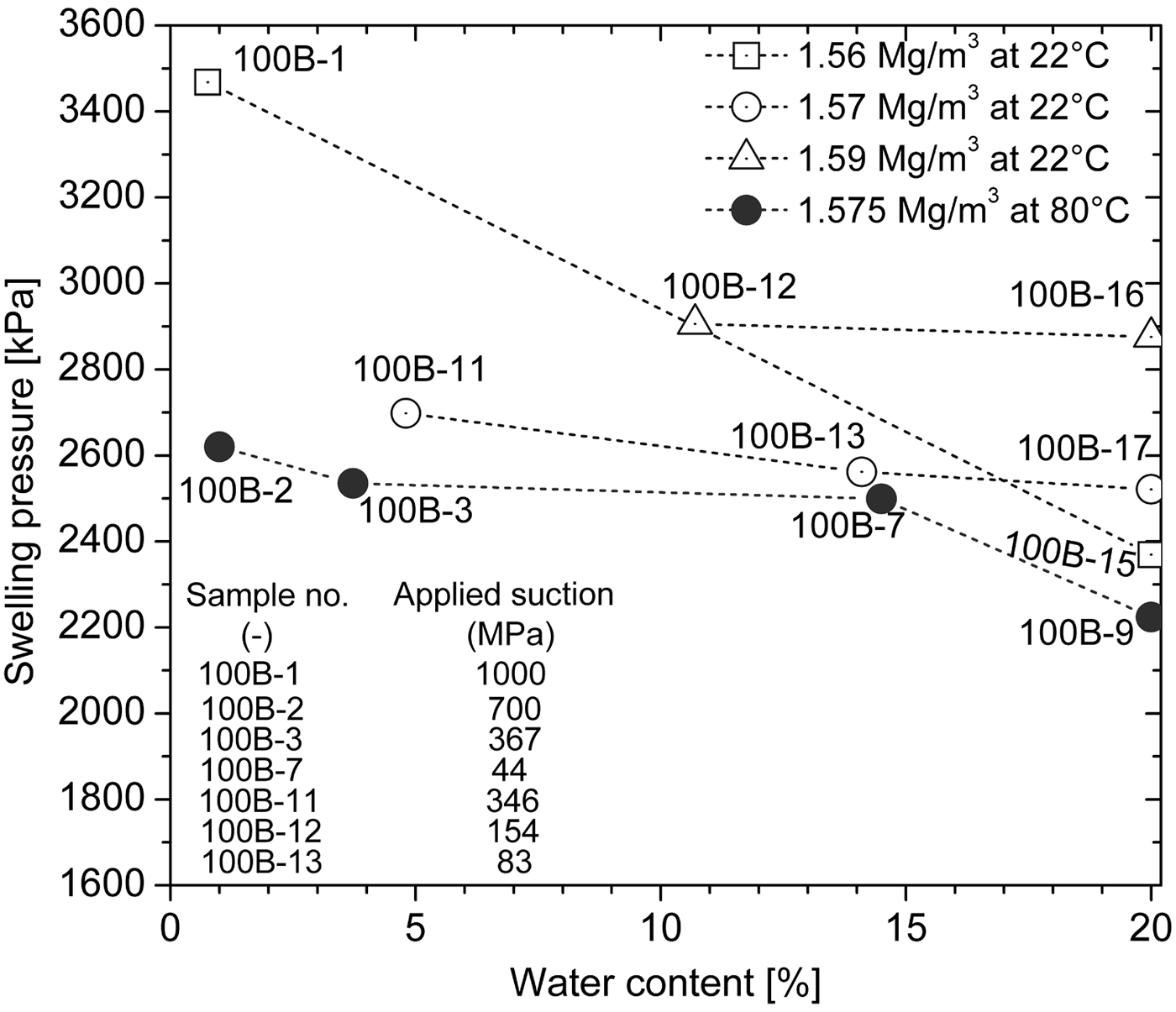
Fig. 9. Dependence of the swelling pressure of compacted bentonite on the water content before hydration for a given temperature and dry density.

The effect of water content before hydration on swelling pressure for a given dry density and temperature is presented in Fig. 9. The swelling pressure increased with decreasing water content before hydration for a given temperature and dry density. This indicates that the desiccated specimens exhibited greater swelling pressure than the reference specimens (100B-9, 100B-15, 100B-16 and 100B-17), as the latter did not undergo preliminary desiccation and had the highest water content. Moreover, the difference in swelling pressure between the desiccated and reference specimens depended on their difference in water content or the applied suction during the preliminary desiccation. The swelling pressure of specimen 100B-1 dried at an applied suction of 1000 MPa increased by 46% compared to reference specimen 100B-15. The swelling pressure of specimen 100B-2 dried at an applied suction of 700 MPa increased by 18% compared with reference specimen 100B-9. The swelling pressures of specimens 100B-11 and 100B-12 dried at applied suctions of 346 and 154 MPa, respectively, increased only by 7% and 1%, respectively. Thus, preliminary desiccation increases the swelling pressure of compacted bentonite (Fig. 9). Furthermore, the increase in the swelling pressure is significant for the compacted bentonite (i.e. specimens 100B-1 and 100B-2) which underwent extreme desiccation at an applied suction of >700 MPa.

The increase in swelling pressure due to preliminary desiccation may be relevant to the influence of desiccation on the fabric of bentonite. Preliminary desiccation, particularly extreme desiccation at an applied suction of >700 MPa, may destroy the dispersed aggregates, resulting in substantial swelling during the subsequent hydration phase. Drying–wetting cycles might significantly increase the swelling of clays and destroy the dispersed clay structure (Osipov et al., 1987; Day, 1994). The destruction of large aggregates and the disorientation of structural elements of the clays increased swelling significantly. A decrease in initial water content or an increase in initial suction might lead to greater swelling pressures for a given dry density, and this is related to the effect of initial water content or suction on the fabric of the expansive clays (Gens & Alonso, 1992; Baille et al., 2010).

Hydraulic conductivity

Figure 10 shows the measured hydraulic conductivities of saturated specimens 100B-2, 100B-7, 100B-9 and 100B-17. Specimens 100B-17 and 100B-9 were the reference samples and thus did not undergo preliminary desiccation and were hydrated at 22°C and 80°C, respectively. The data from Khan (2012) were obtained from a constant-volume permeability test performed at 20°C on a compacted Calcigel bentonite specimen with initial compaction conditions similar to those for specimen 100B-17. The magnitudes of their hydraulic conductivities were similar (1.2 × 10⁻¹³ m/s for the specimen in Khan, 2012, and 7.7 × 10⁻¹³ m/s for specimen 100B-17). However, the hydraulic conductivity of specimen 100B-17 was significantly lower than that of specimen 100B-9 (4.6 × 10⁻¹² m/s), indicating that hydraulic conductivity increases with temperature, given that the two reference specimens had similar dry densities and the same water contents before hydration. This result is consistent with earlier findings that the saturated hydraulic conductivity of compacted bentonites increased with increasing temperature (e.g. Pusch, 1980a; Villar et al., 2010; Ye et al., 2013).

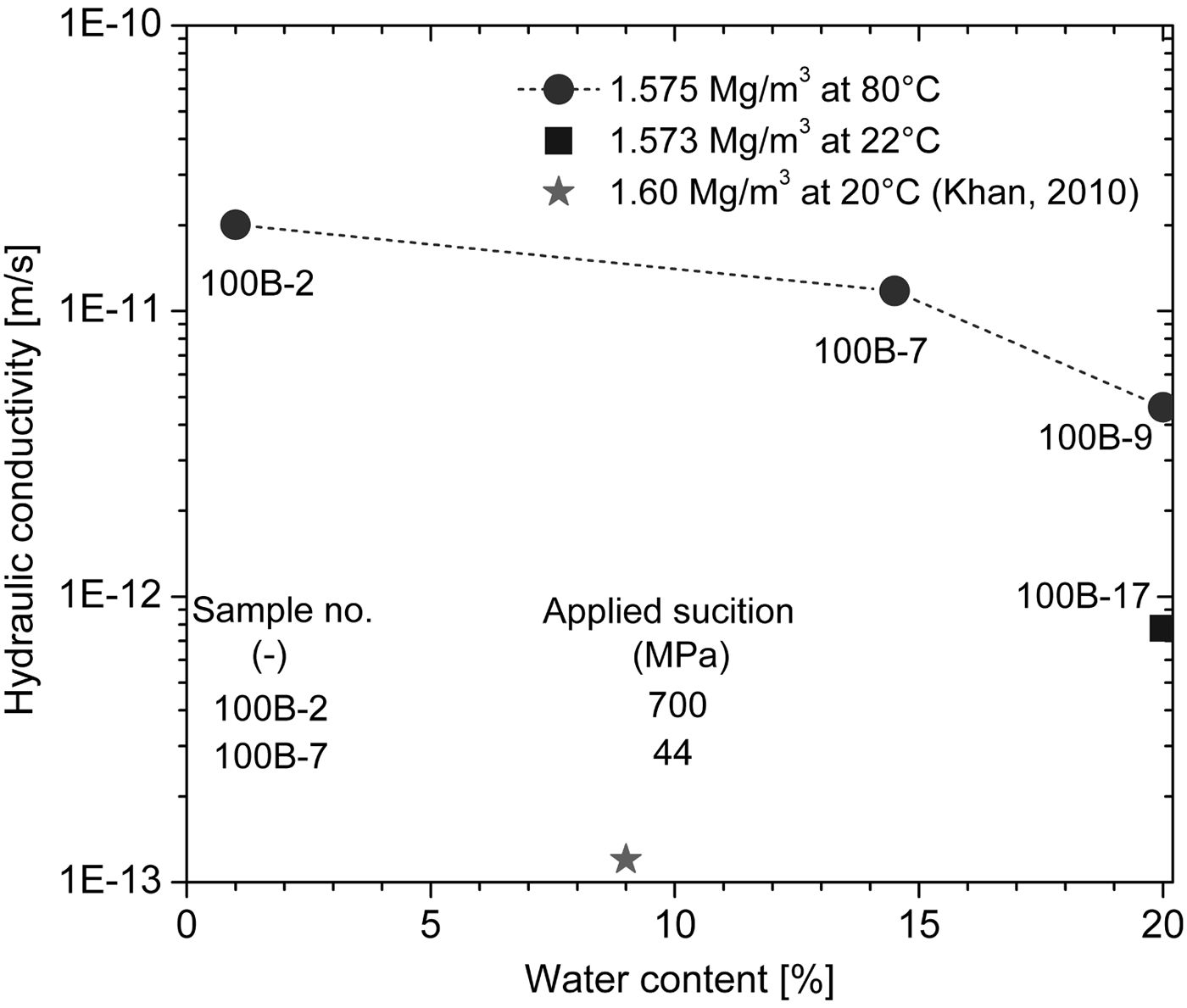
Fig. 10. Dependence of the hydraulic conductivity of compacted bentonite on the water content before hydration for a given temperature and dry density.

At 80°C and a dry density of 1.575 Mg/m³, the hydraulic conductivity increased with decreasing water content before hydration (Fig. 10). Reference specimen 100B-9 had the highest water content (i.e. 20%), but exhibited the lowest hydraulic conductivity (4.6 × 10⁻¹² m/s) compared with specimens 100B-7 and 100B-2. Specimen 100B-17 dried at an applied suction of 44 MPa had a water content of 14.5% and showed a hydraulic conductivity of 1.2 × 10⁻¹¹ m/s. Specimen 100B-2 dried at an applied suction of 700 MPa had the lowest water content (i.e. 1%), but exhibited the highest hydraulic conductivity (2.0 × 10⁻¹¹ m/s). Compared to the hydraulic conductivity of reference specimen 100B-9, the hydraulic conductivities of specimens 100B-7 and 100B-2 increased by 156% and 334%, respectively. These results indicate that preliminary desiccation increases the hydraulic conductivity of compacted bentonite. Moreover, a considerable increase of the hydraulic conductivity occurs if the compacted bentonite (i.e. specimen 100B-2) undergoes extreme desiccation at an applied suction of >700 MPa.

The increase in hydraulic conductivity due to preliminary desiccation may be a result of the fact that the inhomogeneity induced by shrinkage and subsequent temporary unconfined swelling may induce weaker zones with reduced dry densities and slightly higher permeabilities. The volumetric shrinkage due to preliminary desiccation leads to reduced specimen dimensions. Therefore, the initial stage of hydration corresponded to free-swelling conditions (without volume constraint). Hydration of the desiccated specimens under constant-volume condition occurred until the initial radial and vertical gaps were filled with swollen bentonite particles. The initial unconfined swelling results in the redistribution of bentonite particles into the former radial and axial gaps, thus leading to a change in the local dry densities of the specimens. The zone of the former gap may have a reduced dry density as compared to the inner core of the specimen and so might provide a preferential flow pathway. Consequently, the desiccated specimens exhibited greater permeability compared with reference samples without preliminary desiccation. A previous study of the effect of initial technical voids on the hydraulic conductivities of compacted bentonite-based materials indicates that, at the same bentonite dry density or void ratio, the specimens with a larger technical void space showed greater hydraulic conductivity (Wang et al., 2013).

SUMMARY AND CONCLUSIONS

The influence of preliminary desiccation on the subsequent hydro-mechanical behaviour (swelling pressure and hydraulic conductivity) of compacted bentonite was examined experimentally at 22°C and 80°C. For a given level of suction, the equilibrium water content at 22°C is slightly greater than that at 80°C. Moreover, suction rather than temperature dominates the volume shrinkage strain during desiccation. Both the swelling-pressure equilibrium time and equilibrium swelling pressure decrease slightly with increasing temperature, whereas the hydraulic conductivity significantly increases with increasing temperature. In addition, preliminary desiccation increases both the swelling pressure and hydraulic conductivity of compacted bentonite. The increases in the swelling pressure and hydraulic conductivity are significant only if the compacted bentonite undergoes extreme desiccation at an applied suction of >700 MPa.

The present study advances the understanding of the influence of preliminary desiccation on the swelling pressure and hydraulic conductivity of compacted bentonite. The conclusions drawn may provide useful information on designing and constructing for deep geological disposal of HLWs. However, the conclusions in this study are based on the results of Calcigel bentonite specimens with dry densities of 1.56–1.59 mg/m³. Enlargement of the experimental programme to a wide range of initial compaction dry densities and other bentonites would be useful for further assessment of the present conclusions.