Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shangguan, Chong
and
Tamo, Itzhak
2020.
Degenerate Turán densities of sparse hypergraphs.
Journal of Combinatorial Theory, Series A,
Vol. 173,
Issue. ,
p.
105228.
Shangguan, Chong
and
Tamo, Itzhak
2020.
New Turán Exponents for Two Extremal Hypergraph Problems.
SIAM Journal on Discrete Mathematics,
Vol. 34,
Issue. 4,
p.
2338.
Chong, Shangguan
and
Gennian, Ge
2023.
Sparse hypergraphs: From theory to applications.
SCIENTIA SINICA Mathematica,
Vol. 53,
Issue. 2,
p.
187.
Qian, Bingchen
Wang, Xin
and
Ge, Gennian
2023.
Improved Lower Bounds for Strongly Separable Matrices and Related Combinatorial Structures.
IEEE Transactions on Information Theory,
Vol. 69,
Issue. 5,
p.
2801.
Glock, Stefan
Joos, Felix
Kim, Jaehoon
Kühn, Marcus
and
Lichev, Lyuben
2024.
Conflict‐free hypergraph matchings.
Journal of the London Mathematical Society,
Vol. 109,
Issue. 5,

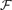 (and the corresponding family of 0–1 vectors) is called
(and the corresponding family of 0–1 vectors) is called